一起学习OT extension的重要文章: Extending Oblivious Transfers Efficiently. 作者是Yuval Ishai, Joe Kilian, Kobbi Nissim, and Erez Petrank, 发表在2003的Crypto上.
- 1. 简介
- 2. 具体协议
- 2.1 协议流程
- 2.2 协议设计原理
- COT和ROT
- 2.2.1 第一步: \(OT^k_m \implies COT^m_k\)
- 2.2.2 第二步: \(COT^m_k \implies ROT^m_l\)
- 2.2.3 第三步: \(ROT^m_l \implies OT^m_l\)
- 3. 协议的安全性证明
- 3.1 Against malicious sender
- 3.2 Against semi-honest verifier
- 4. 实例化Random Oracle
- 5. 总结
- 参考
1. 简介
Motivition: 在这片文章之前的一些结果表明, OT基本不可能规约到开销少的对称原语上, 而只能通过公钥的原语进行构造. 那么人们就会想, 既然OT本身开销不低, 那么能不能通过一些少数量的OT, 基于对称原语构造出大量的OT呢?
人们发现是可以的, Beaver首先给出了一个结果: 可以利用单向函数扩展OT. 但是这个构造是非黑盒的, 所以非常低效, 工程上无法使用.
在Beaver之后就是这篇文章了. 由于这篇文章是第一个实用性的, 所以也算是开山之作. 这篇文章提出的协议(IKNP Protocol)构造是黑盒的, 针对半诚实敌手的时候是pratical的: 每个OT只调用了两次hash函数. 给定 \(k\) 个 base OT, 能构造出 \(poly(k)\) 个OT.
2. 具体协议
我们这里只讨论半诚实敌手模型下的IKNP协议. 在这一小节我们介绍IKNP的具体流程, 以及这个协议的构造思路(作者在文章完全没有提).
2.1 协议流程
协议的目的是, 给定 \(k\) 个OT, 每个消息比特数都是 \(m\)(用 \(OT^k_m\) 表示), 构造 \(m\) 个OT, 每个消息比特数为 \(l\)(用 \(OT^m_l\) 表示).

协议如上所示. 我们简单过一下流程.
-
\(S\) 生成一个向量 \(s\), \(R\) 生成一个矩阵 \(T\).
-
在利用 \(OT^k_m\) 的过程中, \(S\) 扮演了接受者, 用的向量就是第一步生成的那个. \(R\) 扮演了发送者, 用的向量是 \(T\) 的列向量以及列向量与 \(r\) 的异或. S接收到一个矩阵 \(Q\).
-
\(S\) 对 \(Q\) 的行向量进行hash, 再异或上消息值, 发送给 \(R\).
-
由于 \(R\) 没有 \(s\) 的消息, 所以这保证了他没法学到每两个消息的另一个消息, 而只能学到 \(r_j\) 对应的消息.
这只是带大家走一遍, 具体的推导还是得大家动手推导.
2.2 协议设计原理
重新回顾协议的设计目的: \(OT^k_m \implies OT^m_l(m \gg k)\). 作者在原文中是一步登天的. 但是实际上我们可以分为三个步骤.
下面我们分别讲讲这三步是怎么构造的.
COT和ROT
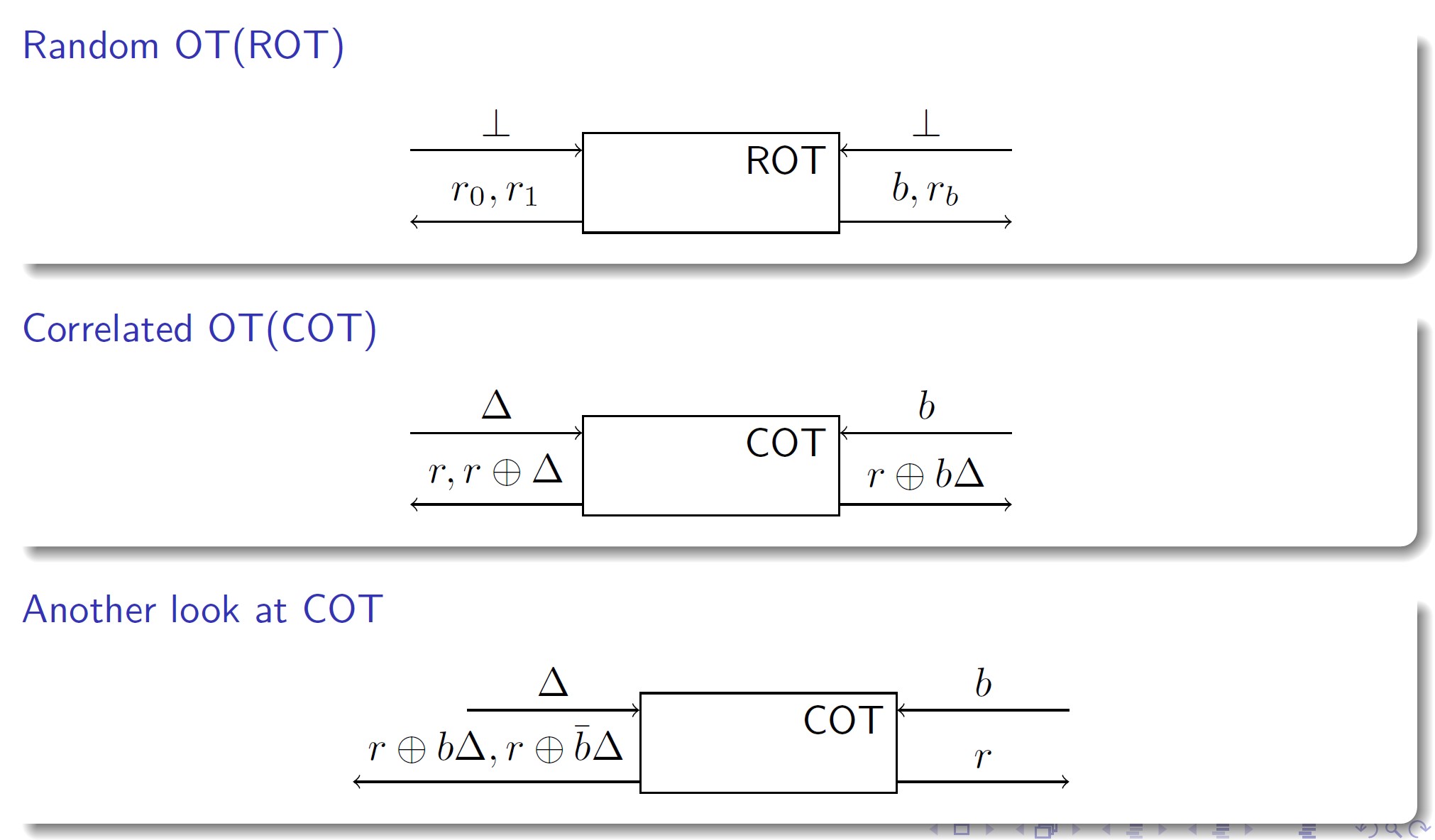
在介绍之前, 我们有必要了解COT和ROT的概念以及作用.
ROT: Random OT. ROT中的Alice和Bob都没有输入. ROT自己生成两个随机数 \(r_0, r_1\), 一个随机比特 \(b\). Alice获得的输出是 \(r_0, r_1\), Bob获得的输出是 \(b, x_b\).
Beaver在95年就提出了这个概念, 并证明了 ROT 可以用于生成 OT.
COT: Correlated OT. 我们考虑Alice输入为 \(\Delta\), Bob输入为 \(b\). COT随后自己产生了一个随机数 \(x\). Alice获得的输出是 \(r, r \oplus \Delta\), Bob获得的输出是 \(b, r\oplus b\Delta\).
在上面的COT中, Alice获得的输出顺序是固定的, 而Bob获得的输出是由 \(b\) 决定的. 我们可以考虑等价的一种COT. Alice获得的输出顺序是由 \(b\) 决定的, 即 \(r \oplus b\Delta, r \oplus \bar{b} \Delta\), 而Bob只会固定的获得一个输出 \(r\). 如下图所示:
2.2.1 第一步: \(OT^k_m \implies COT^m_k\)
我们观察这一步干了什么. OT的数量在这一步由 \(k\) 变成 \(m\), 起到了一个extension的作用. 所以这一步就是这个协议的核心.
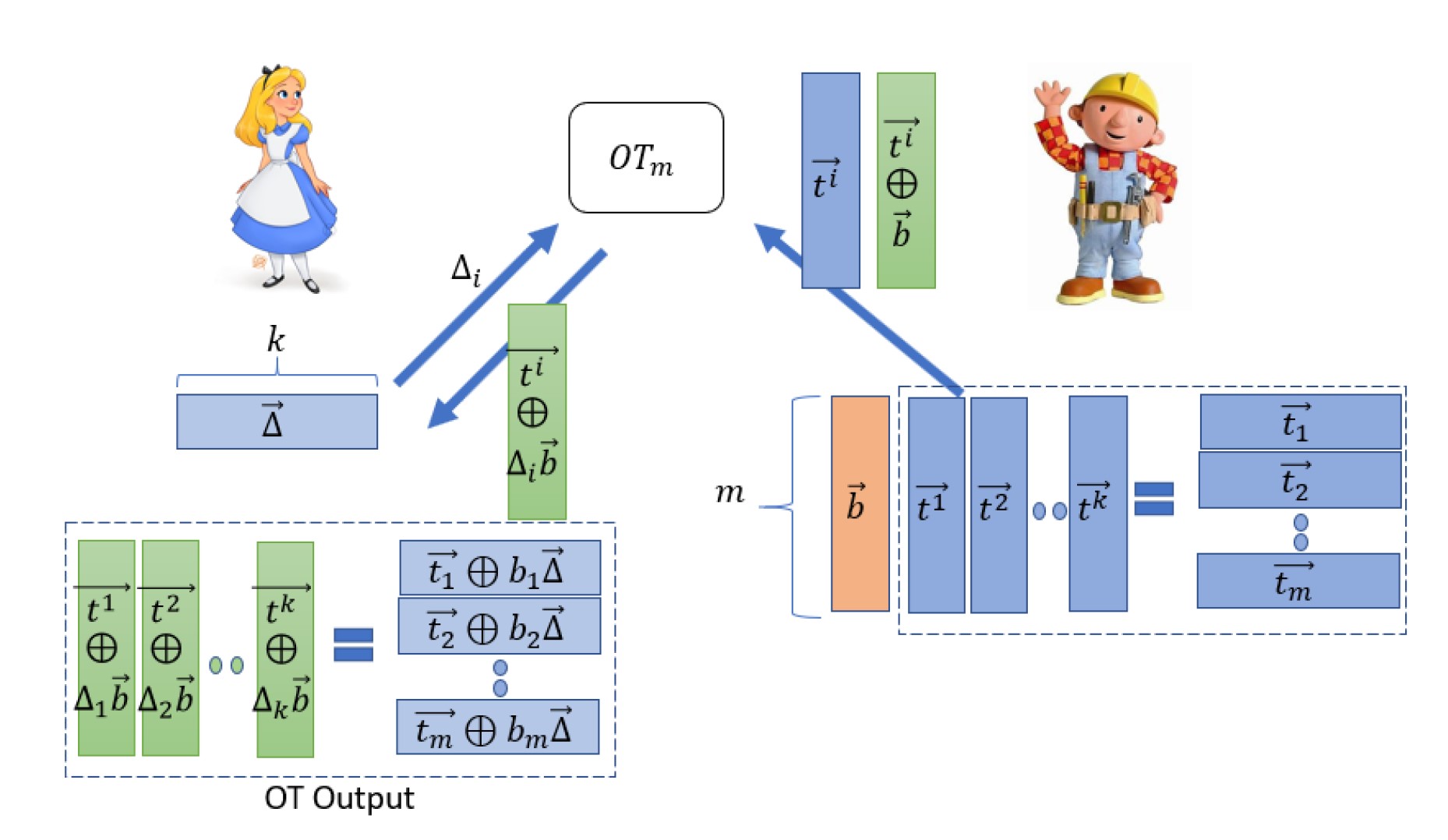
我们从上面的图中更容易看出这个协议内部发生了什么.
我们在2.1节已经讲了这个协议的流程. 所以我们知道Bob在base OT里面扮演了发送者, Alice在base OT里面扮演了接受者, 接收到了一个矩阵 \(Q\).
在拿到 \(Q\) 之后, Alice关注的是行向量, 一共有 \(m\) 个行向量. 对于每一个行向量 \(\mathbf a_i=\mathbf t_i \oplus b_i \Delta\). Alice自己再算出一个值 \(\mathbf b_i = \mathbf a_i \oplus \Delta = \mathbf t_i \oplus \bar b_i \Delta\). 而Bob是持有 \(\mathbf t_i\) 的, 所以这就是我们上面所说的第二种COT. Alice拿到了相关的两个向量, 而Bob拿到了固定的一个 \(\mathbf t_i\). 所以这一步的构造完成.
2.2.2 第二步: \(COT^m_k \implies ROT^m_l\)
这一步我们关注如何打破相关性(break the correlation). 并且顺便我们把比特数也做一个增加.
作者的思路非常的简单粗暴, 就是使用一个Random Oracle. 对RO的输入输出进行规定: \(H: [m] \times \{0,1\}^k\rightarrow \{0,1\}^l\). 其中 \([m]\) 表示 index.
这一步非常直接, 因为Random Oracle本身输出的就是真随机数. 所以是一定没有相关性的.
在实例化的时候, 作者把Random Oracle替换成了一个具有特殊性质的哈希函数(Correlation Robust Hash), 这个我们最后会提到.
2.2.3 第三步: \(ROT^m_l \implies OT^m_l\)
我们离协议成功只差最后一步, 就是转换成真正的OT. ROT转换成OT的工作其实是Beaver在95年就提出的.
有两种情况: 在OT中Bob的选择比特 \(b\) 和 ROT中的选择比特是否相同. 如果相同只需要一轮协议, 否则需要两轮协议. 如下图所示, 左边表示相同情况下的转换, 右边表示不同情况下的转换.

IKNP协议中的最后一条消息利用了左图中的转换.
到此为止我们把协议的构造思路讲清楚了. 下面我们深入协议研究其安全性.
3. 协议的安全性证明
证明分为两个部分, 分别对于 malicious sender, 以及对于 semi-honest verifier. 当然, 当我们考虑一个人是恶意/半诚实时, 我们要求另一个人是诚实的.
形式化的定义请大家参考Lindell: How to simulate it 或者我之前的博客: 如何写好Simulation证明(二): 半诚实模型下MPC的定义 .
3.1 Against malicious sender
在写Simulator之前我们先进行观察. 这里我们需要保证的是: 恶意的Alice不能学到Bob的输入\(\mathbf r\). 我们对Alice拿到的 \(Q\) 进行一个观察. \(Q\) 的每一列, 要么是 \(\mathbf t^i\), 要么是 \(\mathbf t^i \oplus \mathbf r\). 而所有的 \(\mathbf t^i\) 都是独立且随机的, 这相当于一次一密, 是信息论隐藏的. 所以拿到的 \(Q\) 完全是一个随机矩阵. 当然不会学到 \(\mathbf r\) 的任何知识.
下面我们可以写Simulator, 当我们遇到恶意的敌手时, 我们需要注意的是要extract出敌手真正的输入. 因为恶意的敌手不会按照你给他的输入进行.
构造如下:
\(Sim_1\):
-
Run \(S^*\) with a uniformly chosen random input \(\rho\). Let \(\mathbf s^*\) be the input \(S^*\) sends to the \(OT^k_m\) primitive in Step 2.
-
Generate a random \(m \times k\) matrix \(Q\), and feed \(S^*\) with the columns of \(Q\) as the reply from the \(OT^k_m\) primitive.
-
Let \((\mathbf y^*_{j,0},\mathbf y^*_{j,1})\) be the messages sent by \(S^*\) in Step 3. Call TP with inputs \(\mathbf x_{j,0}^*= \mathbf y_{j,0}^*\oplus H(j,\mathbf{q}_j), \mathbf x_{j,1}^*= \mathbf y_{j,1}^*\oplus H(j,\mathbf{q}_j\oplus \mathbf s^*). (1 \leq j \leq m).\)
-
Output whatever \(S^*\) output.
Thm: 这个Sim产生的view和真实世界的完全相同.
3.2 Against semi-honest verifier
在针对半诚实的验证者时, 我们遇到的困难是我们不知道 \(x_{i, 1-r_i}\) 的知识. 但是在写Sim的时候我们可以用 \(0^l\) 去替代. 原因是 RO生成的是真随机数. 通过异或操作一次一密加密了, 所以是Perfect hiding的.
构造如下:
- Choose random \(\rho\) as \(R^*\)'s random tape.
- \(\mathbf s \gets \{0,1\}^k, T \gets \{0,1\}^{m \times k}.\)
- Send \(\mathbf s\) and \(\{\mathbf t^i, \mathbf t^i \oplus \mathbf r\}_{i\in[k]}\) to \(OT^k_m\). Receive the output \(Q\).
- Compute \(y_{j, r_j} \gets \mathbf x_{j,r_j} \oplus H(j, \mathbf q_j), y_{j, 1-r_j} \gets 0^l \oplus H(j, \mathbf q_j \oplus \mathbf{s}) .\)
- Output \((\rho, \mathbf{r}, \{\mathbf t^i, \mathbf t^i \oplus r\}_{i\in[k]} \{\mathbf y_{j,0}, \mathbf y_{j,1}\}_{j \in [m]}, \mathbf x_{j, r_j}).\)
Thm: 这个Sim产生的view和真实世界的统计不可区分.
4. 实例化Random Oracle
通过抽取出特定的性质, 我们定义这样一种哈希函数.

这种hash打破了相关性. 这一串数字都和均匀随机分布不可区分.
5. 总结
在具体写完安全性证明之后, 我相信大家能感受到这个协议构造的精巧. 这个协议把one-time pad(一次一密)用到合适的地方, 达到了Perfect hiding的效果. 这个效果对我们写Simulator具有特别大的帮助.
在如何恶意的敌手时, 这篇文章用到了cut-and-choose技巧. 这个技巧是说, 一开始先进行 \(\sigma\) 次协议. 然后Alice检查其中一部分Bob的输入, 看他有没有骗人. 另一部分则继续用于之后的协议. 开销是十分大的, 我们在这片博客中不介绍.
参考
- Lindell: How to simulate it.
- Nishant Kumar. Techniques in OT extension.
- Ishai et al. Extending Oblivious Transfers Efficiently.