- 1. 概述
- 2. 采样率
- 3. 振幅数值的量化-分贝db
- 4. 预处理--预加重
- 5. 分帧
- 6. 加窗
- 7. 离散快速傅里叶变换
- 8. 梅尔滤波器组
- 9 倒谱分析
- 10, 离散余弦变换
- 11 MFCC
- 12 倒谱均值减
1. 概述
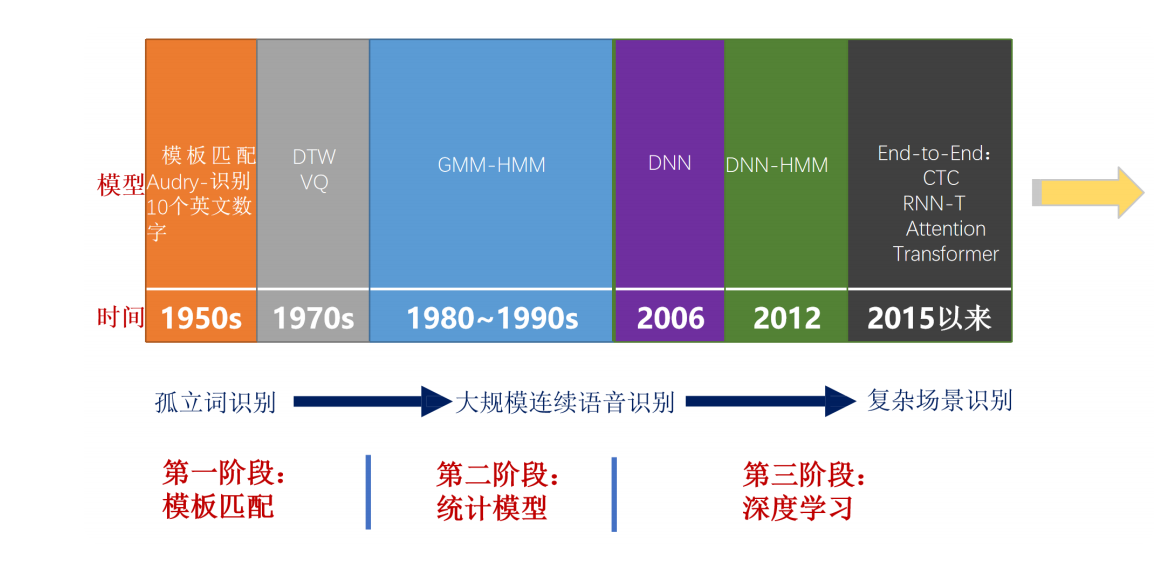
语音产业的上一次爆发出现在20世纪80年代到90年代:隐马尔科夫模型的应用,使大规模连续语音识别成为可能,这意味着用户在人机语音交互,得以摆脱字正腔圆、一词一顿的刻板方式。在过去的十年间,随着深度学习技术的强势崛起和以GPU代表的算力硬件爆发,语音类产品(语音转文字、说话人识别、语种识别等)使用体验得到了显著的提升。新一代Kaldi逐步取代了HTK和Sphinx的统治地位,成为了流行的开源语音工具箱,Kaldi工具箱的出现在很大程度上降低了语音识别技术的门槛,使得语音创业公司能在短时间内开发出一流的语音技术产品。
语音转文字 文字转语音

传统的语音识别与现代的深度学习语音识别:
传统语音识别:分阶段,GMM+HMM、DNN+HMM、N-gram、WFST、Kaldi
深度学习语音识别:端到端,LAS、CTC、RNN-T、HMM-hybird
2. 采样率
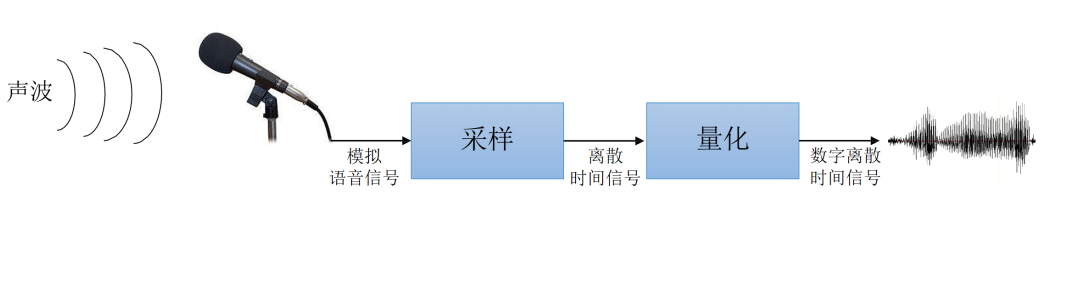
对于采样来说,要确定每秒取多少个点,就是采样率。
波形信号采样中,有一个采样定理,即"如果把原始波形包含的所有频率中最高的频率记为 ,那么以 以上的频率进行采样就可以完全再现原始波形"。采样定理又称奈奎斯特(Nyquist)定理。
人类听觉范围大约是20Hz~20kHz,顺便说一下,音乐CD使用44.1kHz采样率,覆盖了人类听觉的全部范围。
对语音识别来说有效的信息都集中在低频部分,一般我们完全保存8kHz以下的信号,所以多数语音识别系统会使用16kHz的采样率。
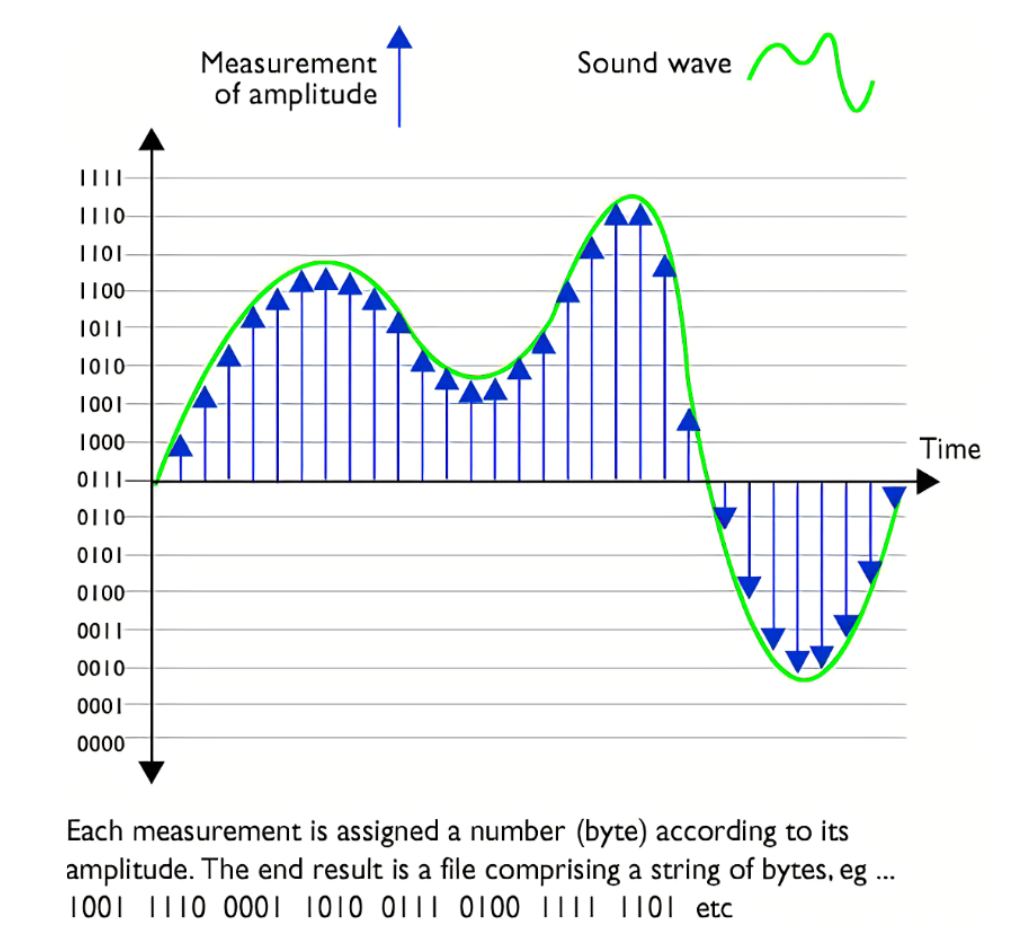
3. 振幅数值的量化-分贝db
说白了就是确定采样点纵轴的值大小;声强以人类能够听到的最小声压20 Pa为基准,所有声强都是这个基准声强的倍数。
人类能够听到的声音中,最大声音的大小是最小声音的100万倍。如果按照这个比例来表声音强度,那么就会因为数值过大而难以二进制编码。因此,通常声压级G来表示,单位是分贝db.
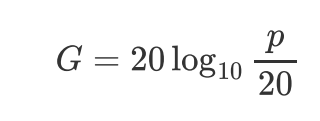
如果用声压级来表示人类听觉上限的声音,大概是120db,这与喷气式飞机引擎轰鸣时的声音相当,因此不在语音识别的考虑范围内。游戏厅或者嘈杂工厂内的声音大概是90db,我们的目标是能够覆盖这个程度的压级,
如果将振幅值二值化,1比特可以表示2倍基准声强,8比特可以表示256倍的基准声强,16比特可以表示65536倍的基准声强。所以使用16比特进行量化处理,就可以表示最高96db的声压级,这个值基本可以覆盖日生活中人类所能听到的声音.
4. 预处理--预加重
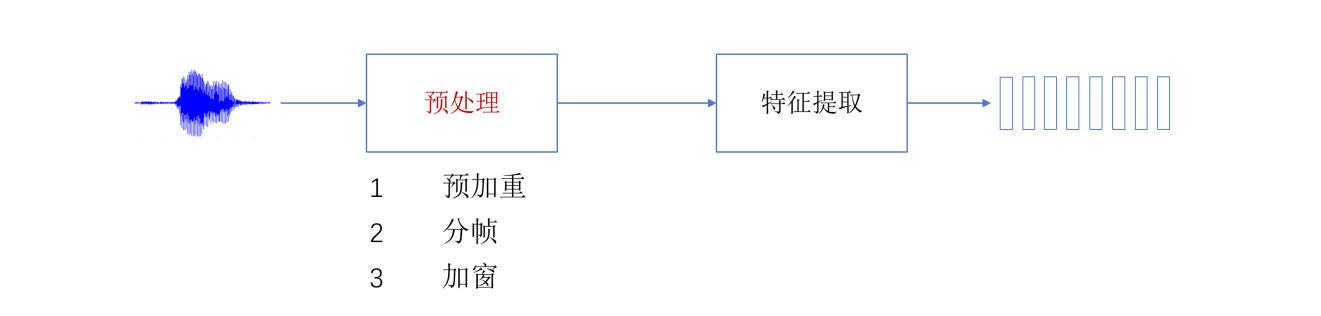

人类的发音器官在向外辐射声波的时候,空气作为语音信号的载体(或者说负载)一方面传播着能量,另一方面则损耗着能量。频率越高,介质对声能量的损耗越严重。
预加重的机制也会发生在人耳的外耳道中,这样一来,我们就能够按照人类的听觉特性,完成对模拟信号的数字化处理。
5. 分帧
常见的方式是:帧移是10ms,帧长是25ms,当然可以根据需求微调;
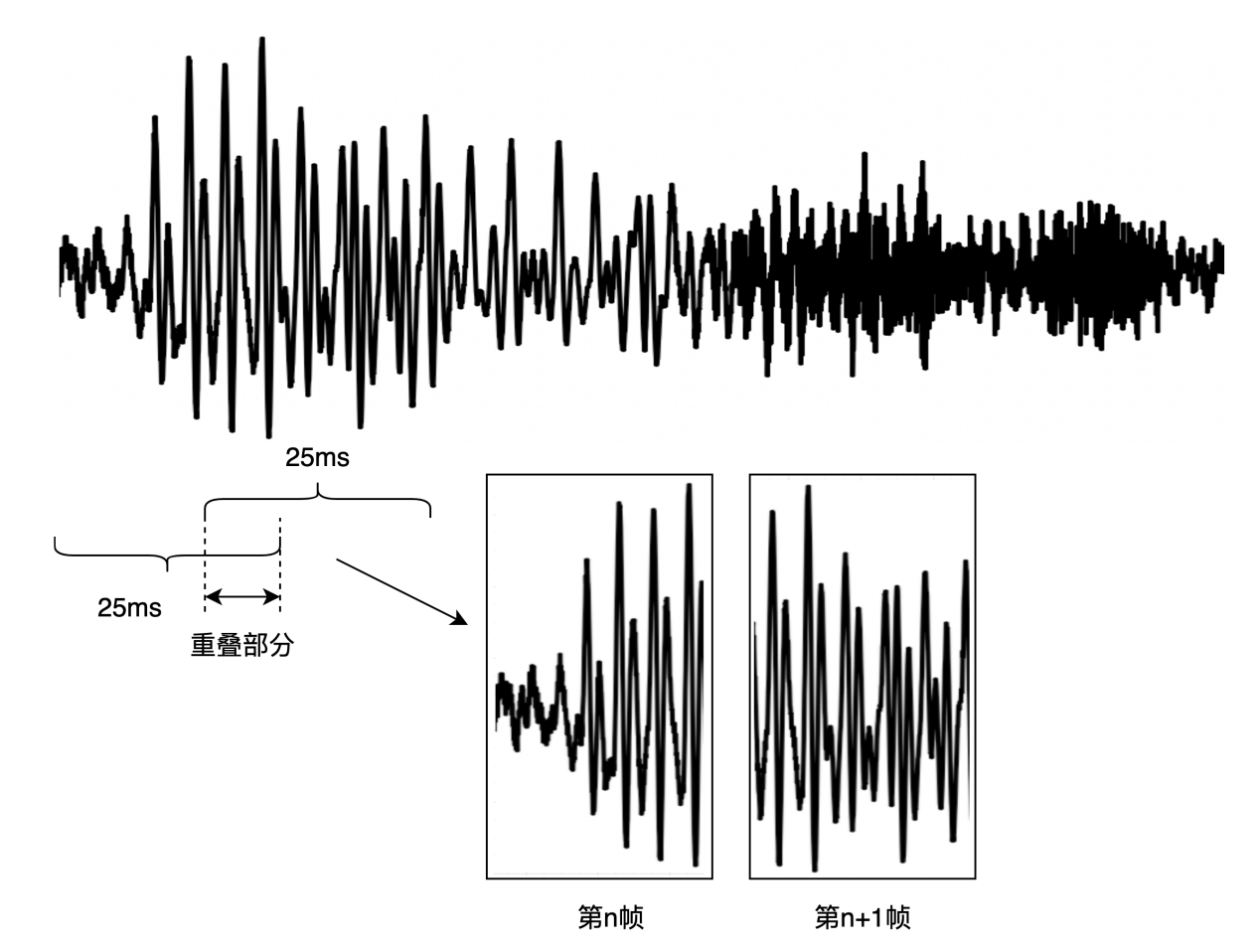
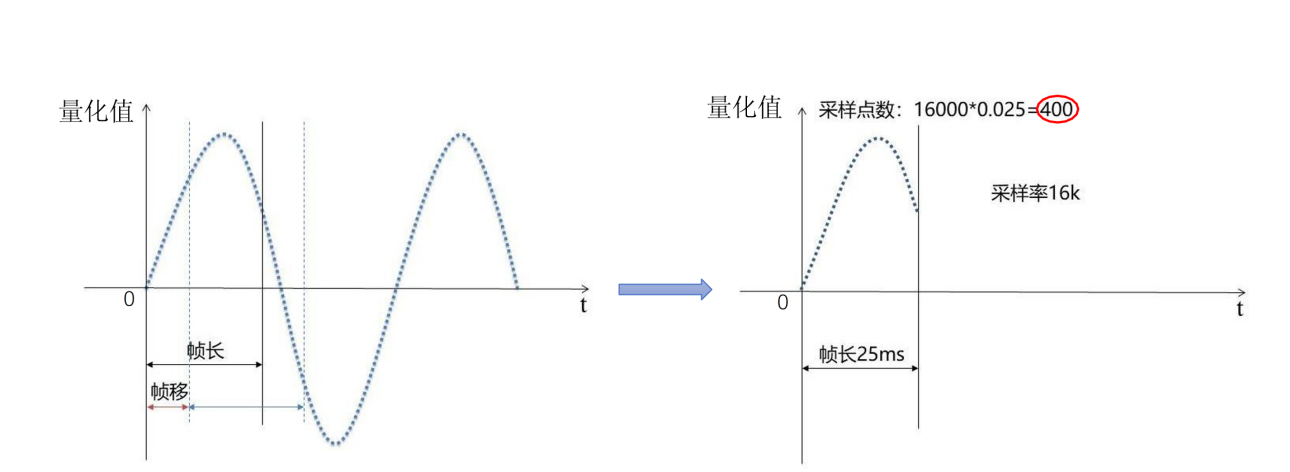
采样率 16k,一帧是0.025s 对应有400个采样点
如上操作,相邻帧会有重叠部分,之所以这么去做的原因:
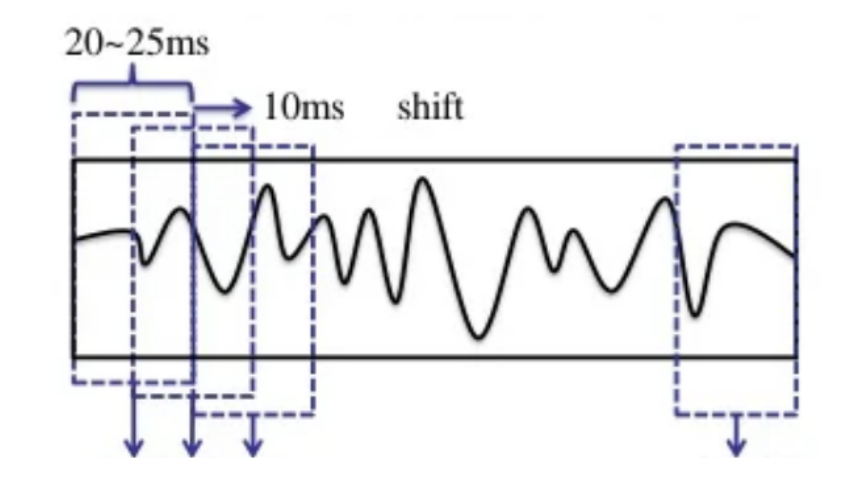
如果每一帧就按照10ms把波形切成数小段,信号在分段的两端就会突然变成0,这样就会出现原始波形所没有的性质。因此我们在分段时,要取25ms大于目标长度10ms的范围。
6. 加窗
当我们前面按照25ms去分帧时,其实依然会出现分段的两端突然变0的情况,所以我们通过设计特殊的加窗函数,来使得分段两端逐渐衰减,这样就可以避免产生突变成0的问题。
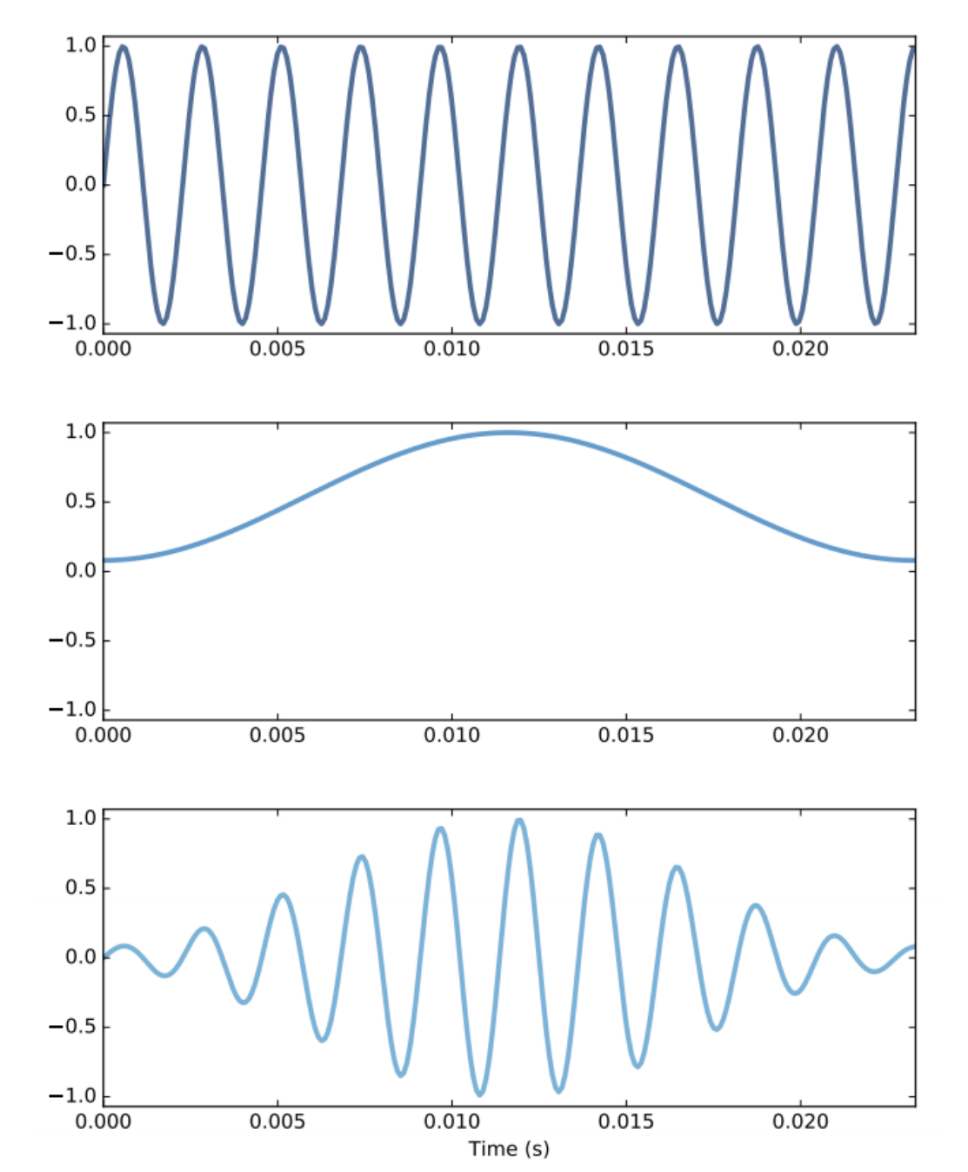
常用的窗函数有:汉明(Hamming)窗、汉宁窗(Hanning)、布莱克曼窗(Blackman)等。
汉明窗能更好地保留原语音信号的频率特性,使用最广泛。
7. 离散快速傅里叶变换
DFT
Discrimi Fourior Transform
对经过分帧加窗处理的语音信号实施傅里叶变换,就可以计算其频率成分了。
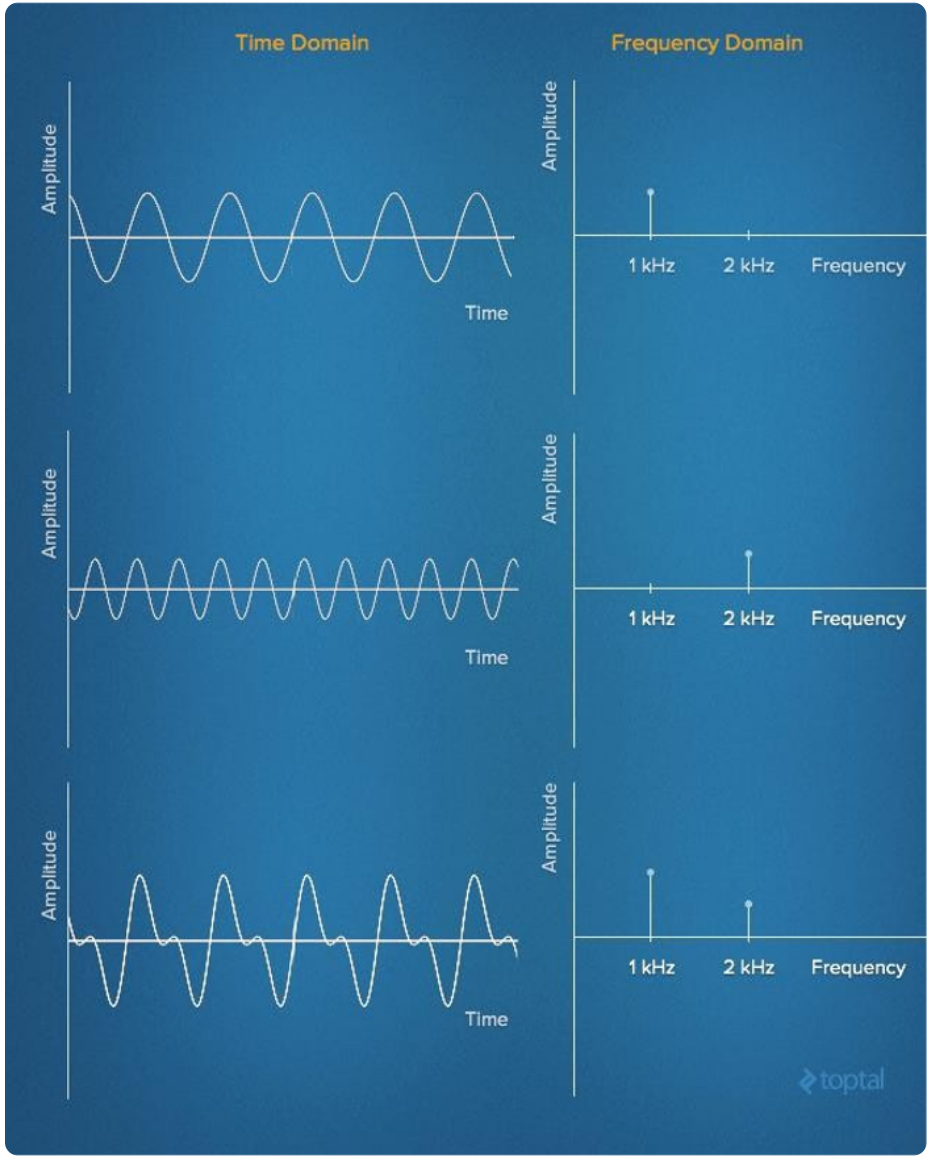
语音由基本频率的谐波加权和所构成,将时间轴信号转换成多个单一频率信号的叠加,从而把同一信号从时间轴转换成频率轴表示的处理,就是傅里叶变换。
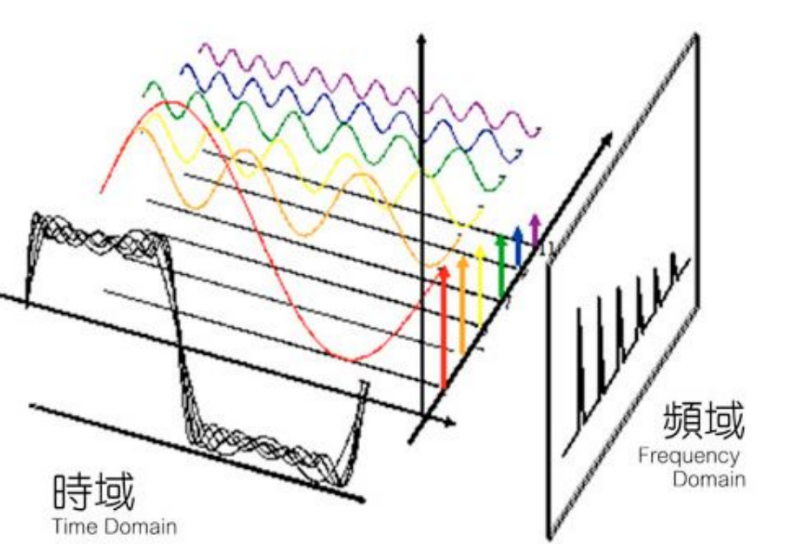
时域 转换成 频域
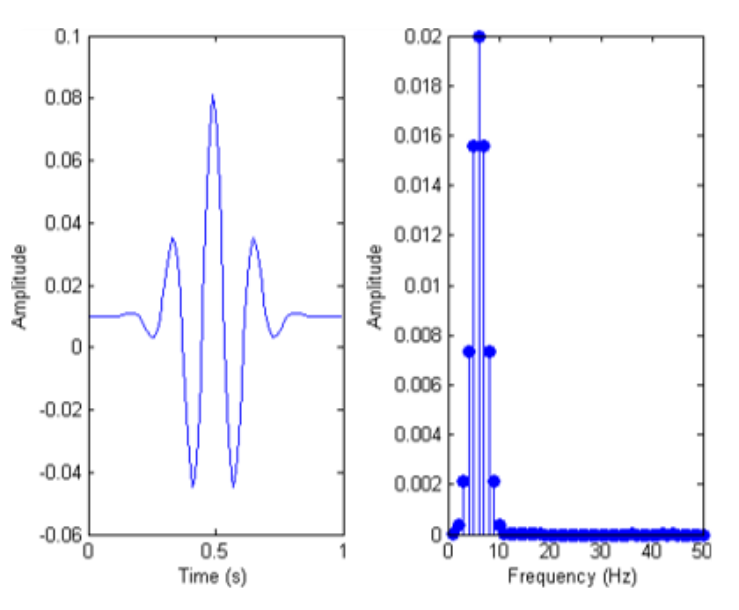
需要注意的是,由于信号是经过数字化处理的离散值,所以要实行离散快速傅里叶变换;得到的结果是复数频谱,计算复数频谱的绝对值(实部和虚部的平方和再开方),就可以得到能量谱。
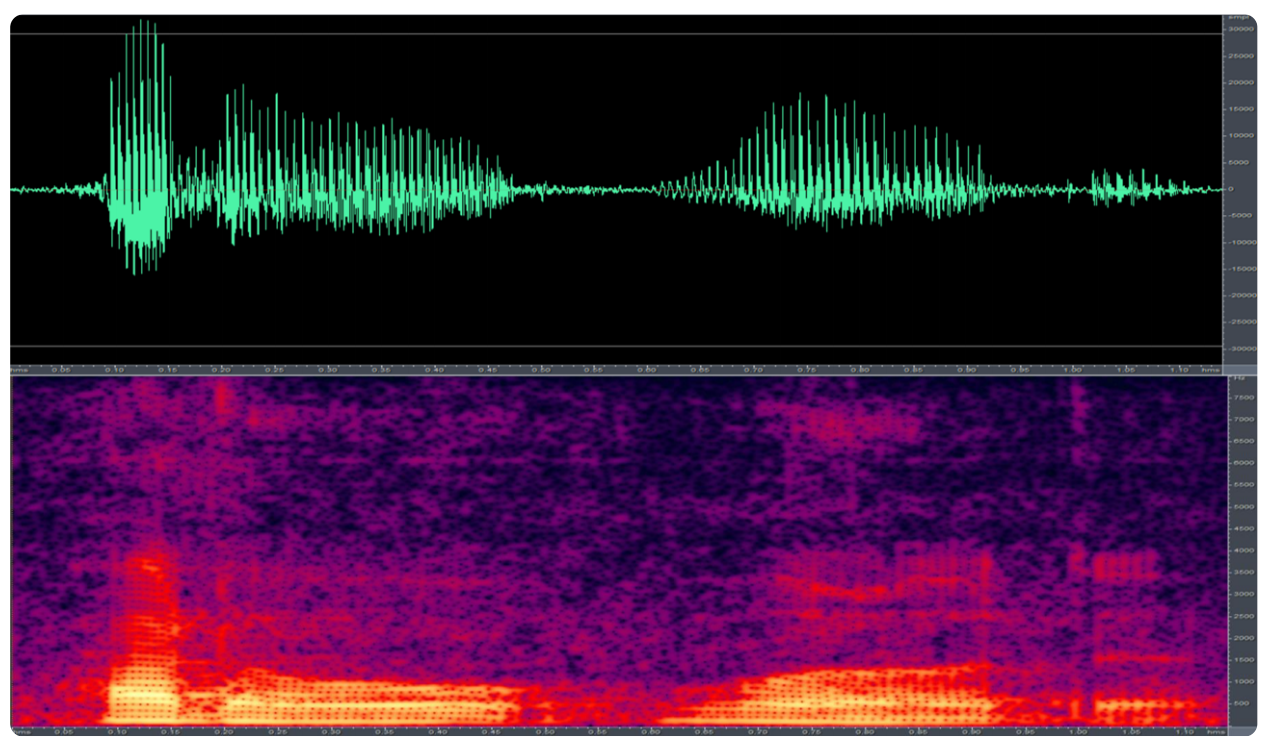
8. 梅尔滤波器组
Mel-Frequency Analysis
对语音信号进行分析的目的,并不是获取纯粹的物理信息,而是获取一种与人类听觉机制近似的信息。目的是让机器听懂人话
虽然人类是通过耳蜗内鼓膜的振动来感知声音频率的,但听觉系统感知的不是特定频率的声音,而是能感知很多特定频域范围的声音(排列着很多不同的毛细胞)。另外,听觉系统感知到的这个频域范围的宽度,随着频率的升高而越来越宽。
需要一组滤波器 感受不同频率的声音
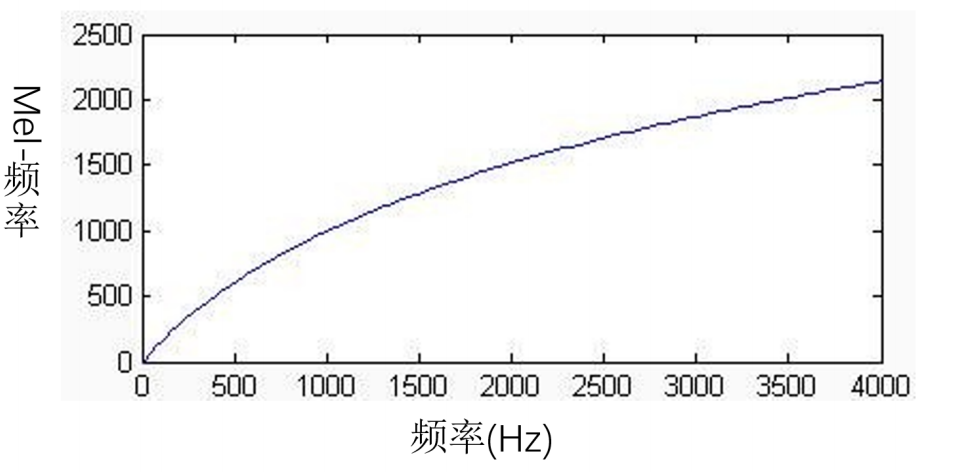
对于低频声音哪怕有很小的频率高低变换也可以感觉得到,但是对于高频声音,没有达到一定程度的频率变化,耳朵是听不出来的。所以我们是不是应该模仿人类的这个特点来对数据进行特征提取!
梅尔刻度就是根据这个原理实现
梅尔刻度:用于把人类对声音频率高低变化的感知程度进行定量化表示
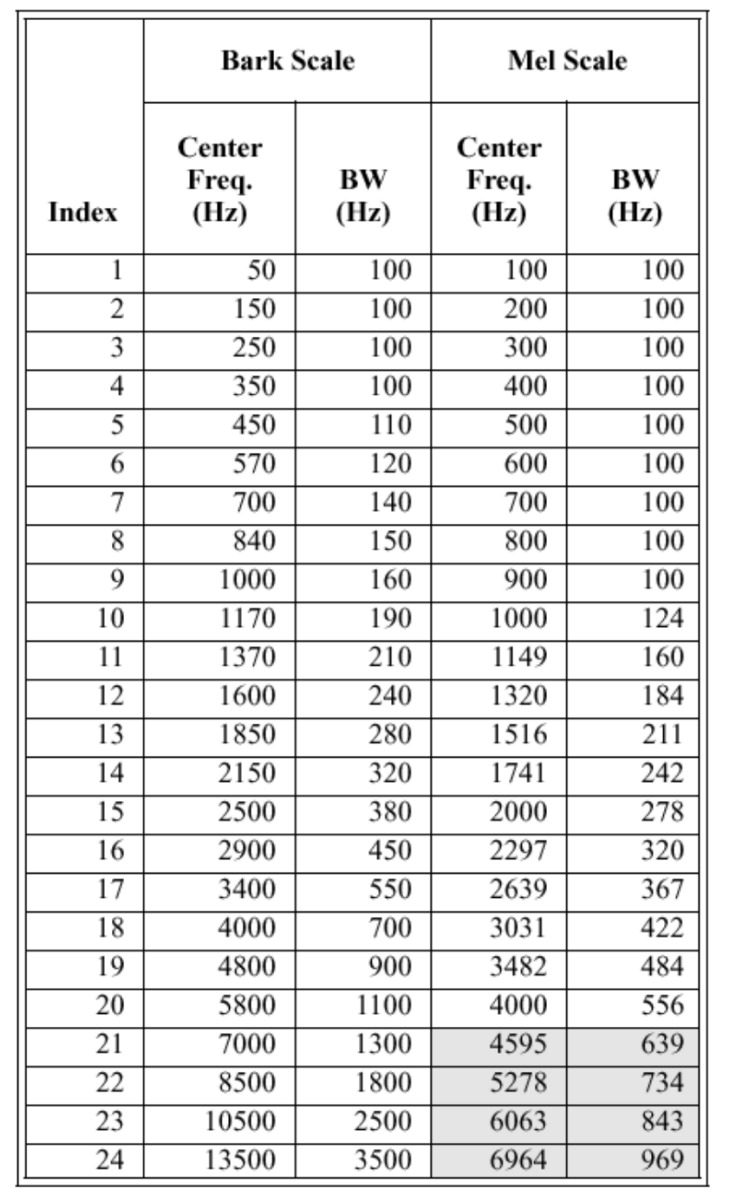
按照梅尔刻度对每帧能量谱的数据进行测量,具体就是把每个梅尔刻度单位区间的数据,通过滤波器组(filter bank)对附近的数据取平均,得到的结果就很接近人类所感知到的频率信息了。反映了人类对音高感觉(频率越高,感觉越迟钝)。
研究者根据心理声学实验得到了类似于耳蜗作用的一组滤波器组,模拟人耳对不同频段声音的感知能力。多个带宽不等的三角滤波器组成Mel频率滤波器组,线性频率小于1000Hz的部分为线性间隔,而线性频率大1000Hz的部分为 对数间隔。
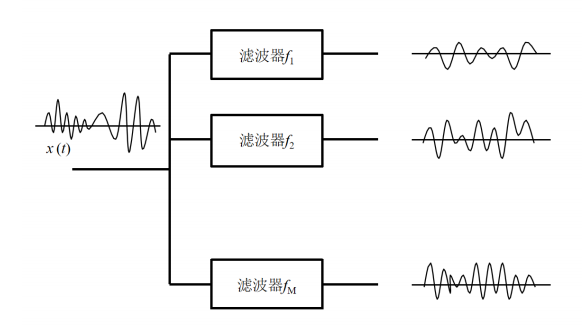
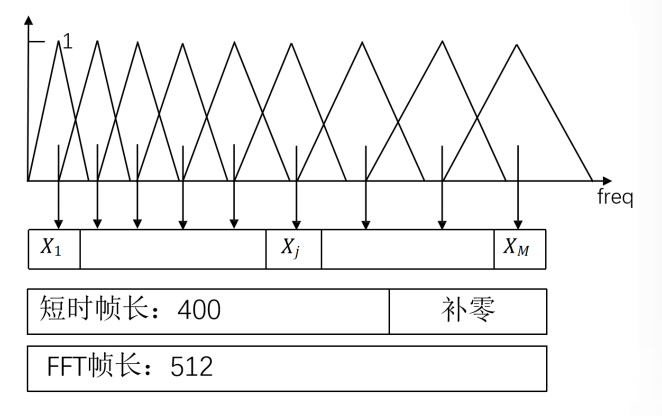
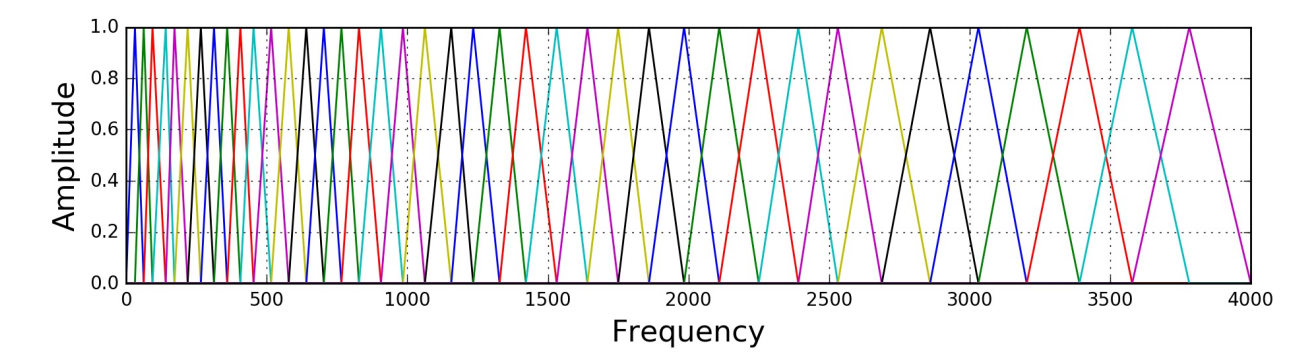
在语音识别中,针对8kHz的有效频率范围,通常会设定24个滤波器
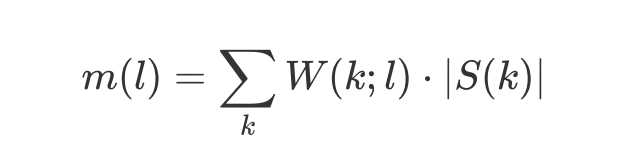
这里m(l)是第l个梅尔滤波器的值
w(k;l)是三角窗函数
|s(k)|表示能量谱,k为频率
人类的知觉是对数刻度的,所以最后需要对梅尔频带谱取对数。 (重点)
9 倒谱分析
Cepstrum Analysis
spec倒过来 ceps
通过前面的处理,我们可以采用与人类听觉相对应的方法,来获取声音的频率成分信息。但是,在这些频率中,声源信息和声道信息仍然是混杂在一起的。
声源信息本身我们可以看成是脉冲信号,而语音就是声源信号和声道发音等价滤波器卷积得到的结果。----重点
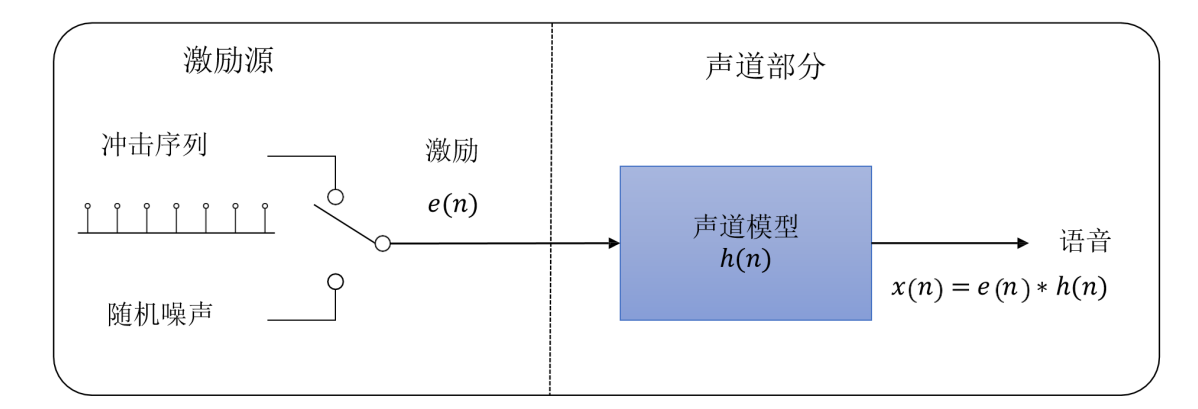
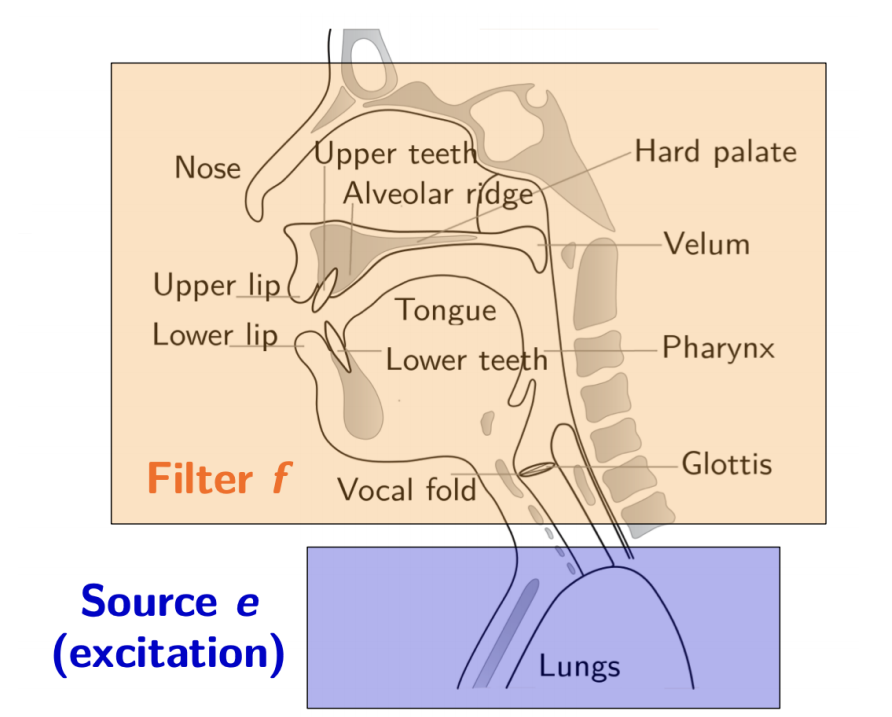
倒谱分析想要做的事情是把声道发音等价滤波器在每一帧的情况,给提取出来 ----重点
也就是得到人们常说的包络信息
之前有对语音信号进行傅里叶变换,傅里叶变换可以把卷积运算转换成乘法运算;然后使用梅尔滤波器组将信号转换成梅尔频带谱,再对梅尔频带谱取对数,这样就把乘法运算转换成了加法算了。

10, 离散余弦变换
Discriminate Cos Tranform
在经过梅尔滤波器组处理后是离散值,取对数也依然是离散值。所以此时才会用离散余弦变换DCT,以进一步分解频率成分,
DCT(离散余弦变换)变换就是DFT(离散傅里叶变换)变换的一种特殊形式
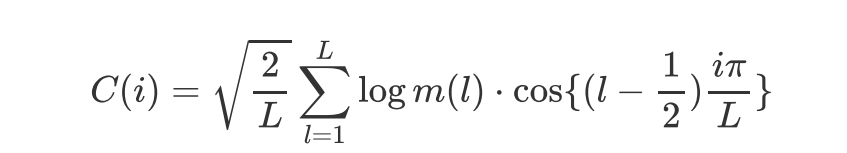
经过这样的处理后得到的信息称为倒谱(cepstrum)
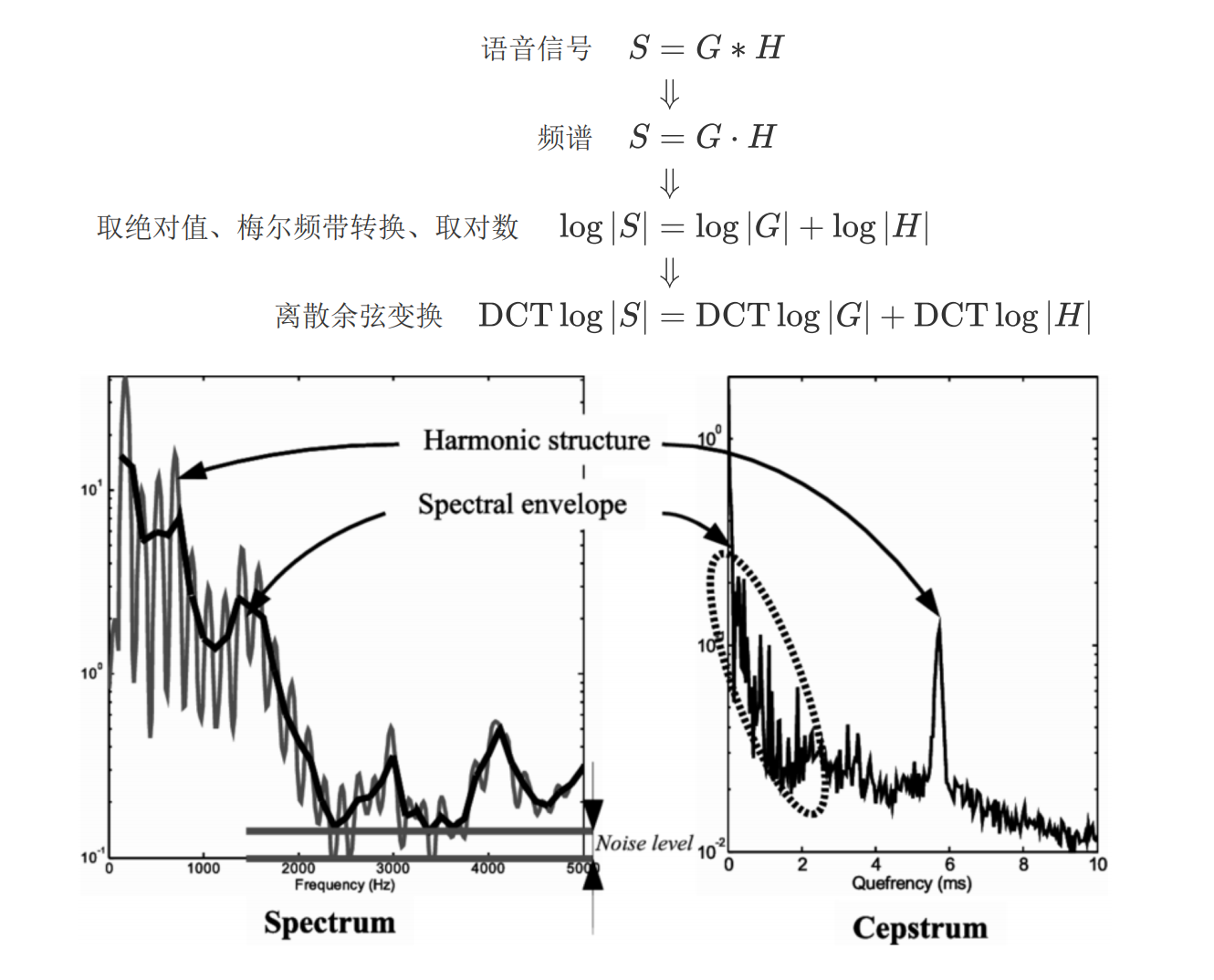
倒谱的理解:把声音频谱看作信号,进行傅里叶变换得到的信息。----重点 频谱的频谱
11 MFCC
Mel Frequency Cepstral Coefficient

频谱包络(低频)相当于声道发音等价滤波器的传递特性H ,频谱的细节(高频)相当于声源信号G,倒谱的目的就是将二者分离出来。
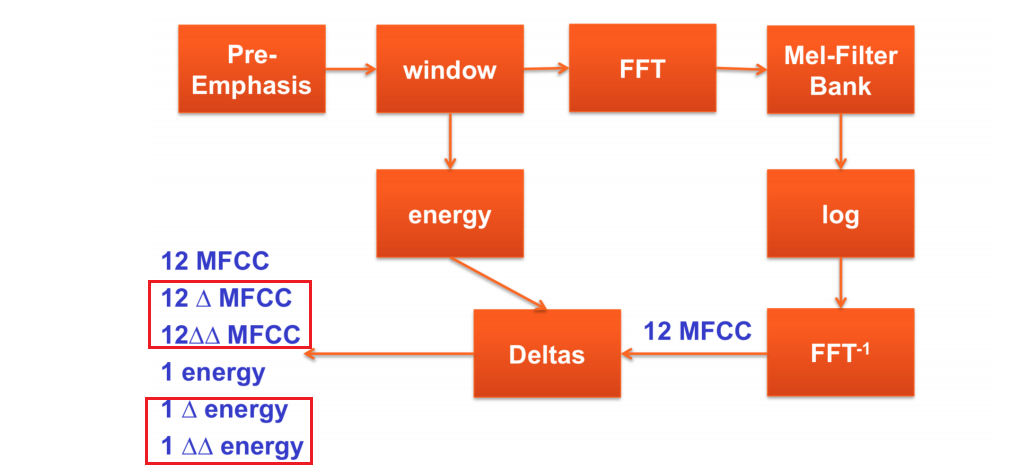
所以可以直接用频谱包络从低频开始顺序取12维信息,将其作为该信号区间的语音信号特征。这个就是梅尔频谱倒谱系数MFCC。
MFCC的值是经过离散余弦变换的结果,所以各个成分是相互独立的;值的各成分相互独立,即它们是不相关的这个性质,在HMM声学模型的得分计算或HMM的训练中是非常有利的
元音:
MFCC与某一帧信号的频谱的轮廓信息是一致的,所以在元音的识别中,可以直接使用。
辅音:
辅音的特征反映的是频谱的变化,所以还需要获取MFCC的变化量, △MFCC

(每一帧)语音信号的强度(能量)是声音的大小,虽然与当
前的发音是什么没有关系,但是不同的发音会导致在(不同帧
或时刻)中能量的变化模式不同,所以能量的变化量---△能量, 以及变化量的变化量----△△能量
也会作为信号特征被加到特征向量,
把这些特征汇总起来,语音特征就是每10ms用39个维度实数来表示的向量。

12 倒谱均值减
Cepstrum Mean Subtraction
作为识别对象的语音信号通常会掺杂噪声,所以如果能够去除这些噪声,就可以提高识别性能。
噪声有两种,一种是背景噪声,好比说话时边上有人打呼噜,是与语音信号叠加在一起;
另一种是比如通过麦克风或某种介质传递时带来的失真噪声,就好像经过了某个滤波器,一直会存在。前者是加性噪声,后者是乘性噪声。

CMS这个方法是对语音全体求倒谱均值,然后从各帧的倒谱中减掉倒谱均值。
因为是在倒谱上做减法,所以相当于去除了乘性噪声,而对全体取均值,则相当于对不同说话人或加性噪声也同时进行了处理