C++U7-08-拓扑排序-编程知识

C++U7-08-拓扑排序

news/2025/1/21 0:56:41/文章来源:https://www.cnblogs.com/jayxuan/p/18238671

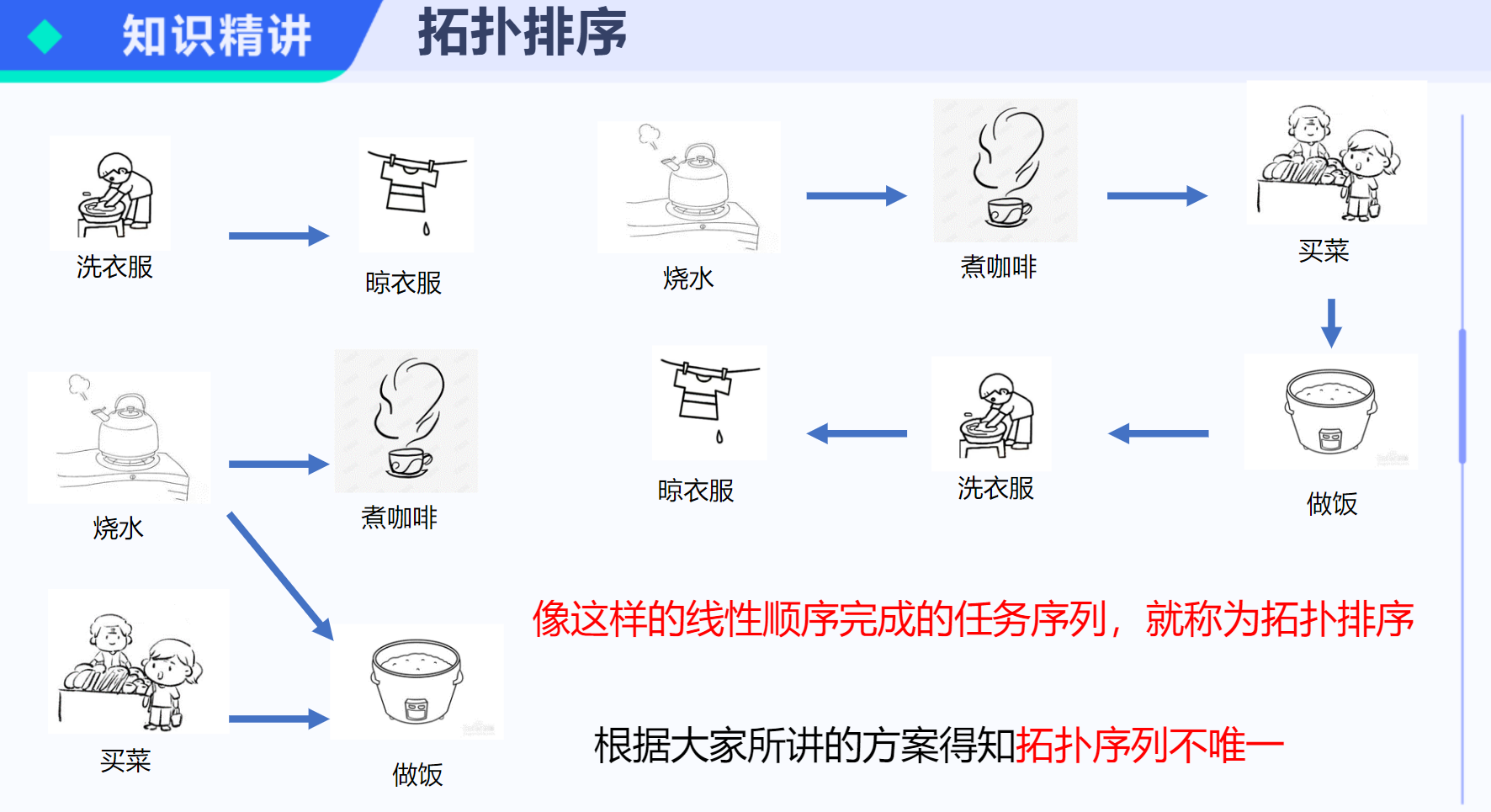
拓扑：是指把实体抽象成与其大小形状无关的点，把连接实体的线路抽象成线，研究这些点线之间的相连关系。而表示点和线之间关系的图就被称为拓扑结构图。

拓扑学原本是一个数学概念，描述的是几何图形或空间在连续改变形状后还能保持不变的性质，它只考虑物体间的位置关系而不考虑它们的形状和大小。

此外，在计算机网络中，拓扑结构是指用传输介质互连各种设备的物理布局，反映出网络中各实体的结构关系，是建设计算机网络的第一步，是实现各种网络协议的基础，它对网络的性能，系统的可靠性与通信费用都有重大影响。

学习拓扑可以先看这个视频：非常好的视频：【拓扑排序在依赖关系解析中的应用【计算机设计大赛参赛作品】】 https://www.bilibili.com/video/BV1iT421y7KT/?share_source=copy_web&vd_source=d28947bf5669866688dc057b3c41b450

[【拓扑排序】摄像头]

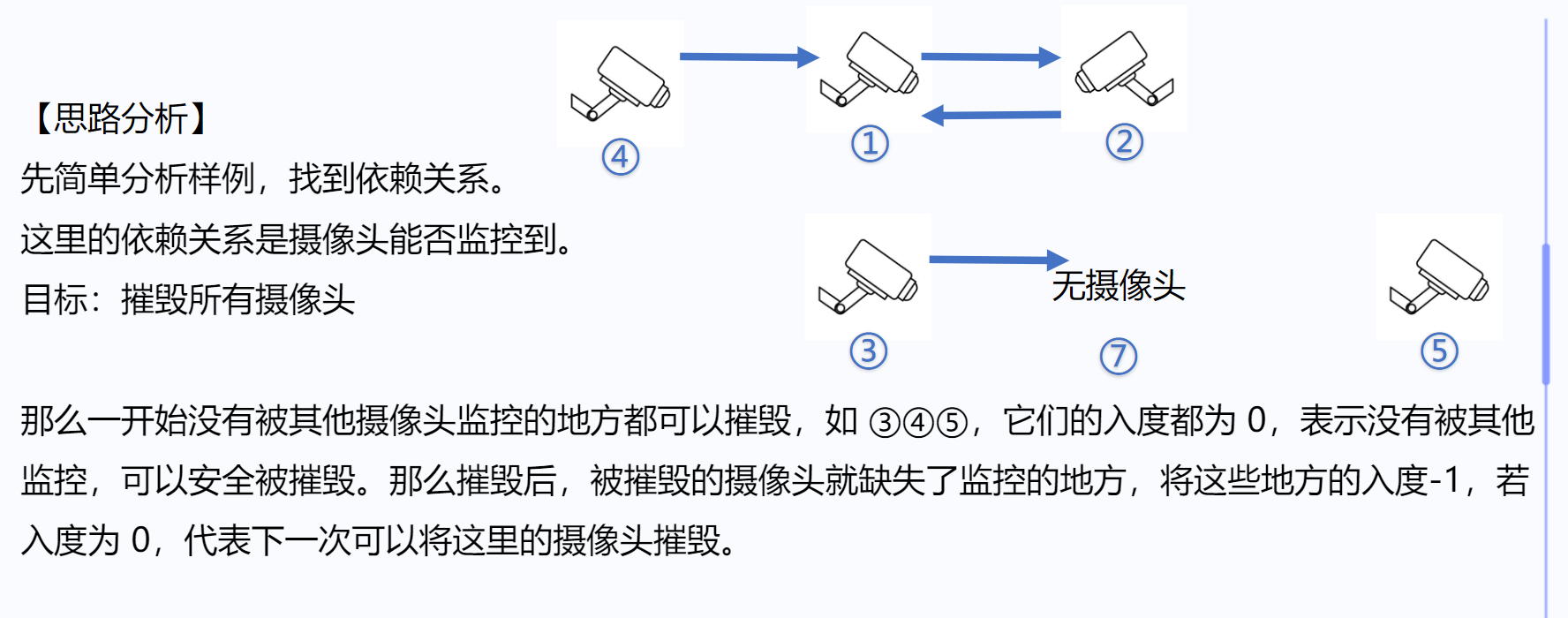
【算法分析】
想要破坏所有的摄像头，那么一定是先将没有被监控的摄像头给摧毁，然后这些摄像头被摧毁后可能会出新出现一些没有被监控的摄像头，然后把这些摄像头摧毁。不断重复上面的步骤，直到不能再摧毁摄像头为止。这是一个典型的拓扑排序的问题，采用拓扑排序解决。【参考代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e2 + 9;
bool vis[maxn];
int deg[maxn];
vector<int> ve[maxn];
int main() {int n;cin >> n;for (int i = 0; i < n; i++) {int x, m;cin >> x >> m;while (m--) {int y;cin >> y;ve[x].push_back(y);deg[y]++;}}queue<int> q;for (int i = 1; i <= n; i++) {if (deg[i] == 0) {vis[i] = 1;q.push(i);}}while (q.size()) {int r = q.front();q.pop();for (int i = 0; i < ve[r].size(); i++) {int y = ve[r][i];if (--deg[y] == 0) {q.push(y);vis[y] = 1;}}}int num = 0;for (int i = 1; i <= n; i++) {if (!vis[i]) num++;}if (num) cout << num;else cout << "YES";return 0;
}

View Code

[【拓扑排序】判环]

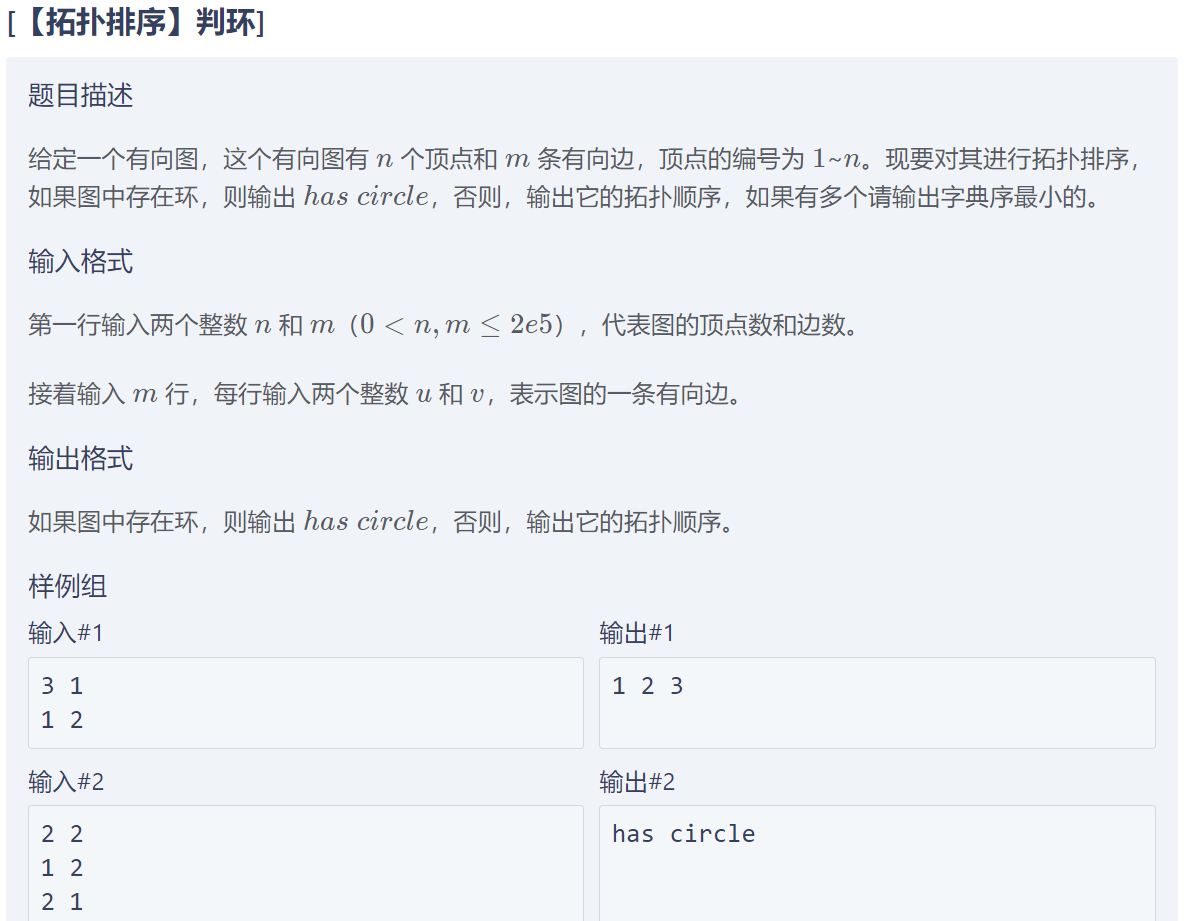
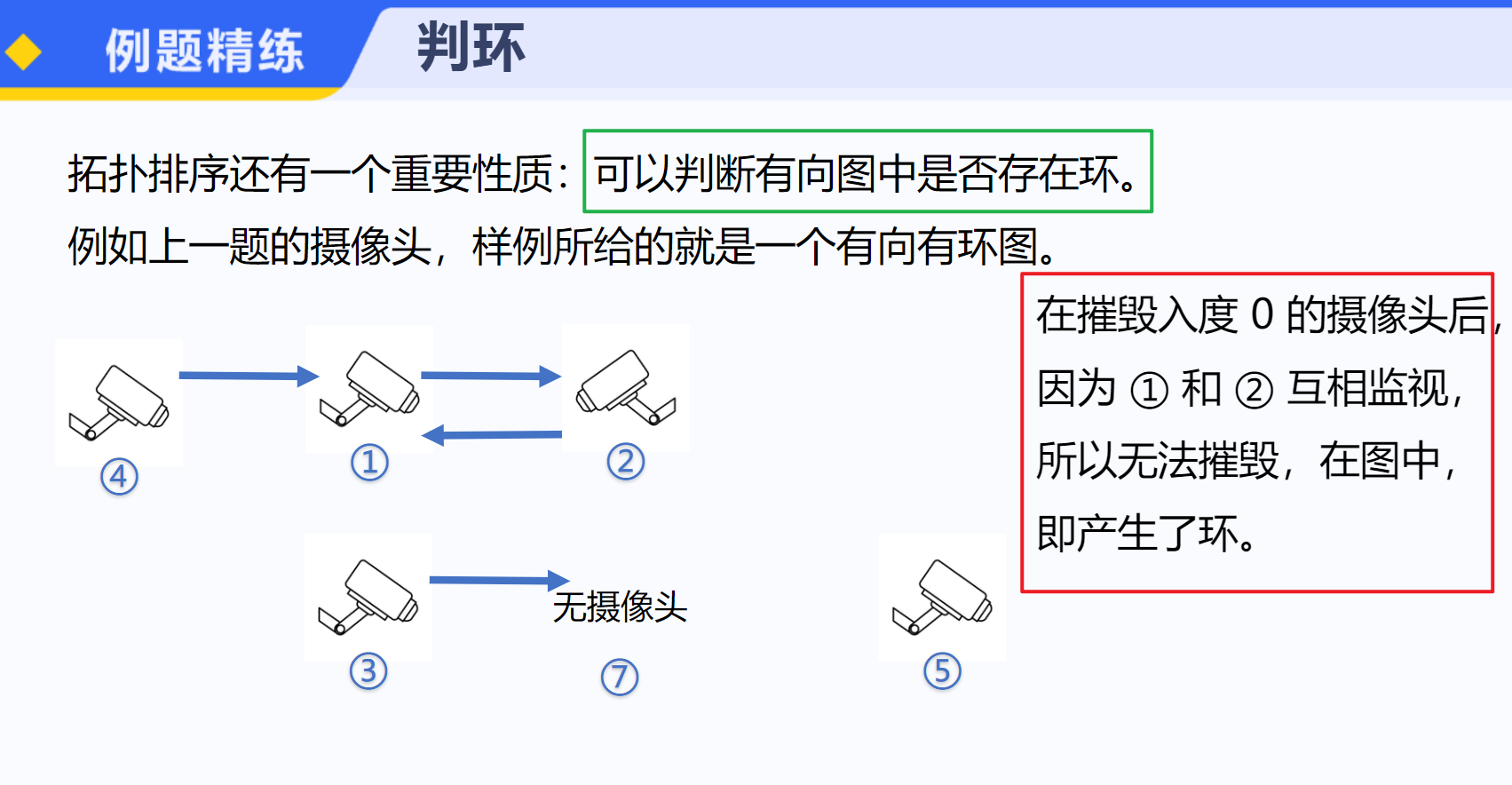
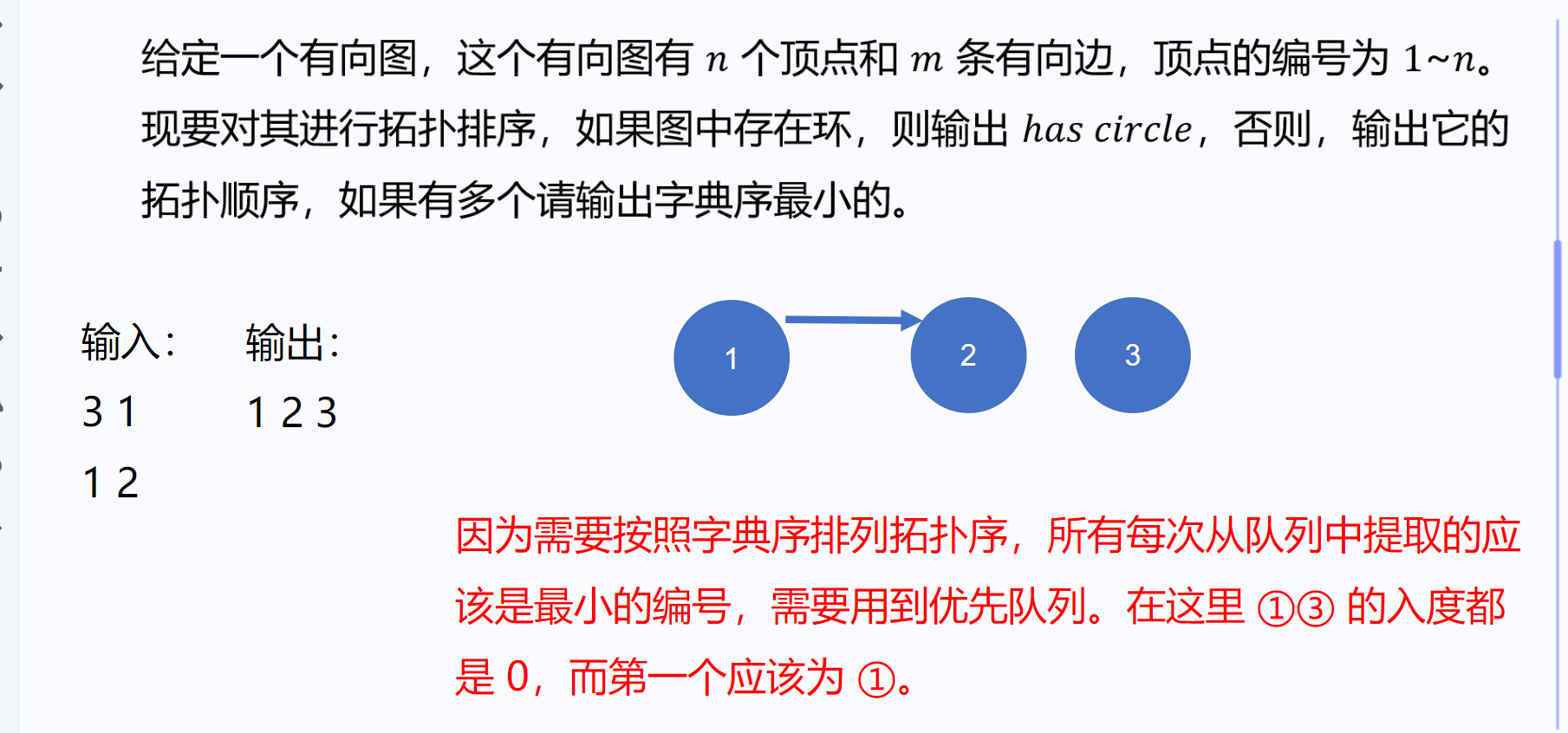
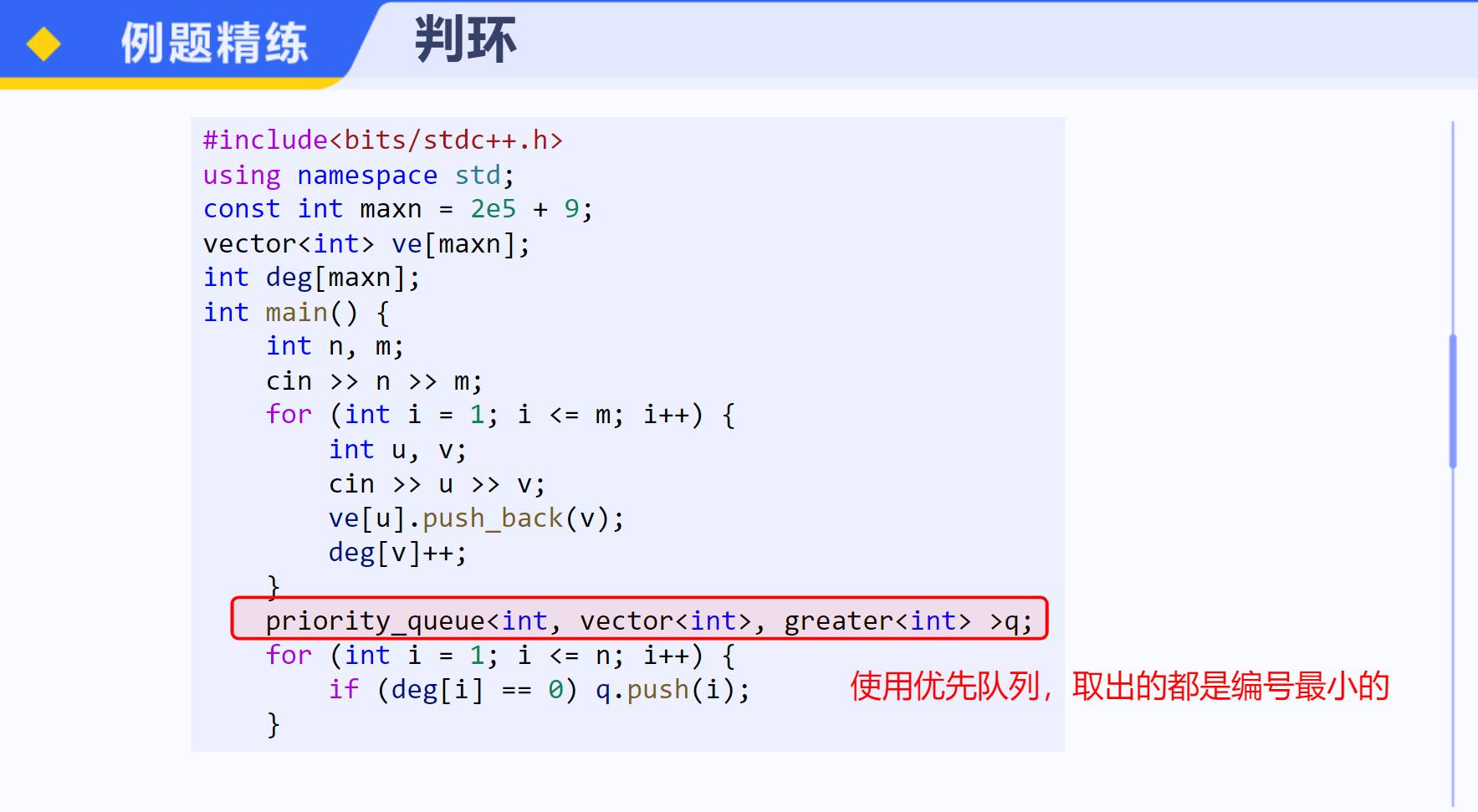
【算法分析】
这题和模板拓扑排序的区别就是要输出字典序最小的，也就是我们每次要在能选择中选择最小的，因此可以用优先队列来维护能选的顶点，这样每次只需要选堆顶的元素。【参考代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 9;
vector<int> ve[maxn];
int deg[maxn];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= m; i++) {int u, v;cin >> u >> v;ve[u].push_back(v);deg[v]++;}priority_queue<int, vector<int>, greater<int> >q;for (int i = 1; i <= n; i++) {if (deg[i] == 0) q.push(i);}vector<int> ans;while (q.size()) {int r = q.top();q.pop();ans.push_back(r);for (int i = 0; i < ve[r].size(); i++) {int y = ve[r][i];if (--deg[y] == 0)q.push(y);}}if (ans.size() != n) cout << "has circle";else {for (int i = 0; i < ans.size(); i++) cout << ans[i] << " ";}return 0;
}