4. 从前序与中序遍历序列构造二叉树
题目描述:给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例:
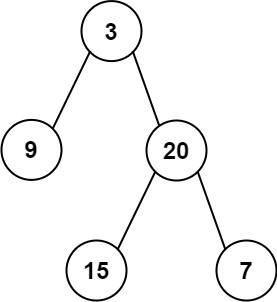
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
初见想法
- 不懂如何构建树
- 不知道前序和中序还原树的规则
- 即使知道规则也不知道如何用于构建树
GPT代码
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildTree(preorder, inorder):if not preorder or not inorder:return Noneroot_val = preorder[0]root = TreeNode(root_val)root_index = inorder.index(root_val)root.left = buildTree(preorder[1:root_index+1], inorder[:root_index])root.right = buildTree(preorder[root_index+1:], inorder[root_index+1:])return root# 示例输入
preorder = [3, 9, 20, 15, 7]
inorder = [9, 3, 15, 20, 7]# 构建二叉树
root = buildTree(preorder, inorder)# 遍历二叉树
def postorder_traversal(node):if node:postorder_traversal(node.left)postorder_traversal(node.right)print(node.val)postorder_traversal(root)
思路理解
- 首先,建树就是要定义一个有值,左右指针的对象
- 由于是递归地构建树,所以要有终止条件,也就是当可供构建的序列其中一个为空时就停止构建,返回空
而且,两个序列一定同时为空或不为空,因为这两个序列分别代表以该节点为根节点的树的前中序遍历。

- 所谓前中后序遍历,实际上指的是根节点被遍历的次序,描述的就是左右两个孩子中间插入一个父节点,这时候有三个空位,插在哪个就是对应的遍历。
所以,通过前序遍历的第一个元素,我们可以确定这两个序列所对应的根节点,进而可以在中序遍历中找到根节点的位置,这样又可以分出左右两棵子树。
这时的关键就在于如何确定两棵子树拥有的前中序遍历,这就要涉及到一个关键的变量——根节点的位置,因为这涉及到左右子树拥有的元素。
如上图所示,前序遍历是根-左-右,中序遍历是左-根-右,所以在中序遍历中找到根节点的位置后,就可以根据其位置,获取前序和中序遍历的子树数组,因为遍历是递归的,所以在原有树下的遍历顺序在子树下也一样。 - 整个过程都在利用到建构树的对象。
- 递归函数的返回就是根节点。