这里写目录标题
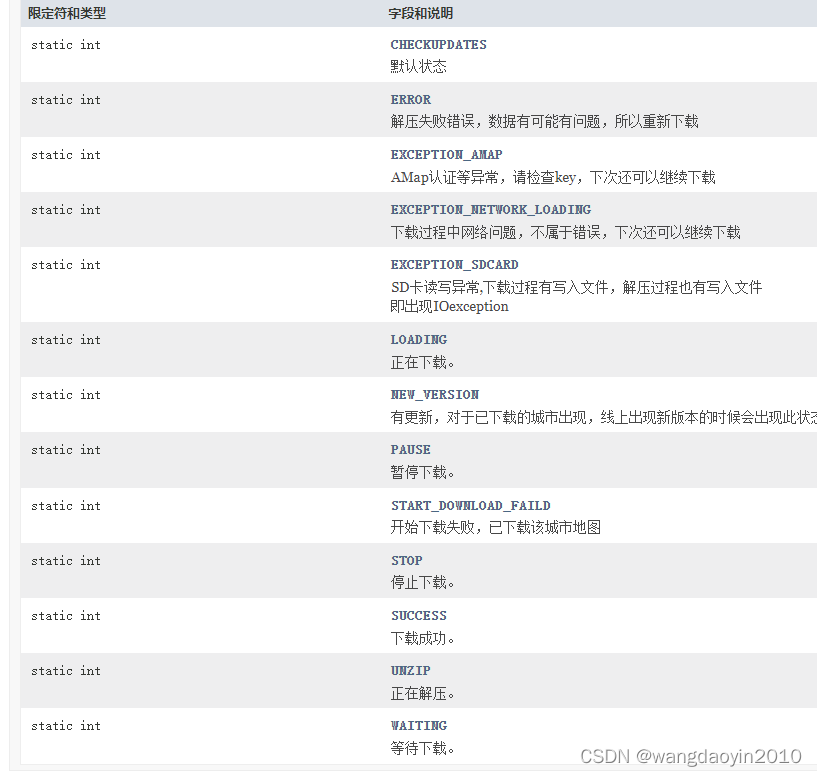
- 图的基本概念和术语
- 基本概念和术语1
- 基本概念和术语2
- 图的类型定义
- 抽象数据类型定义
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 二级目录
- 二级目录
- 二级目录
图的基本概念和术语
基本概念和术语1

V代表顶点的有穷非空集合
E代表边的有穷集合

n为顶点

有向图中的箭头又叫做弧
网:权也就是 某种场合下赋予边的某种意义
邻接:是指两个顶点之间的关系
圆弧括号针对于无向图
尖括号针对于有向图 并且代表i邻接“到”j j邻接“于”i

度:该顶点的边的数目
有向图中 度等于入度(指向某个顶点)和出度(从某个顶点指出)之和

基本概念和术语2

路径是顶点序列 用顶点表示
路径长度有两种表示方式
对于没有权的路径 路径长度是边数之和
对于有权的路径 路径长度是权重之和

形成回路就是回路
对于简单路径 除了起点终点可以重复之外 中途没有重复的结点 叫做简单路径
进而有了简单回路的概念
但是只要中途有重复 那么就是非简单路径

连通图 对于任意两个顶点 总有路径可以相互通达
有向的连通图称作强连通图
无向的连通图称作连通图


顶点或者边是子集即可

极大连通子图 也就是图中某个子图 是连通的 并且 顶点数目已经达到了最大 再加顶点就不会连通了
极大连通子图别称连通分量

有向图对应着叫强连通分量 这里连通子图的判断一定要注意双向

极小连通子图 边已经达到了最小 再删除任意一条边 就不连通了
图的类型定义
抽象数据类型定义