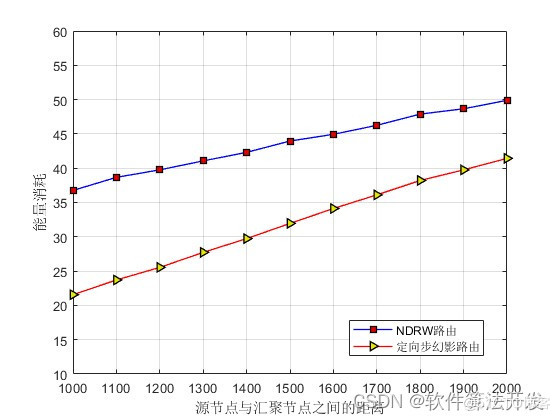
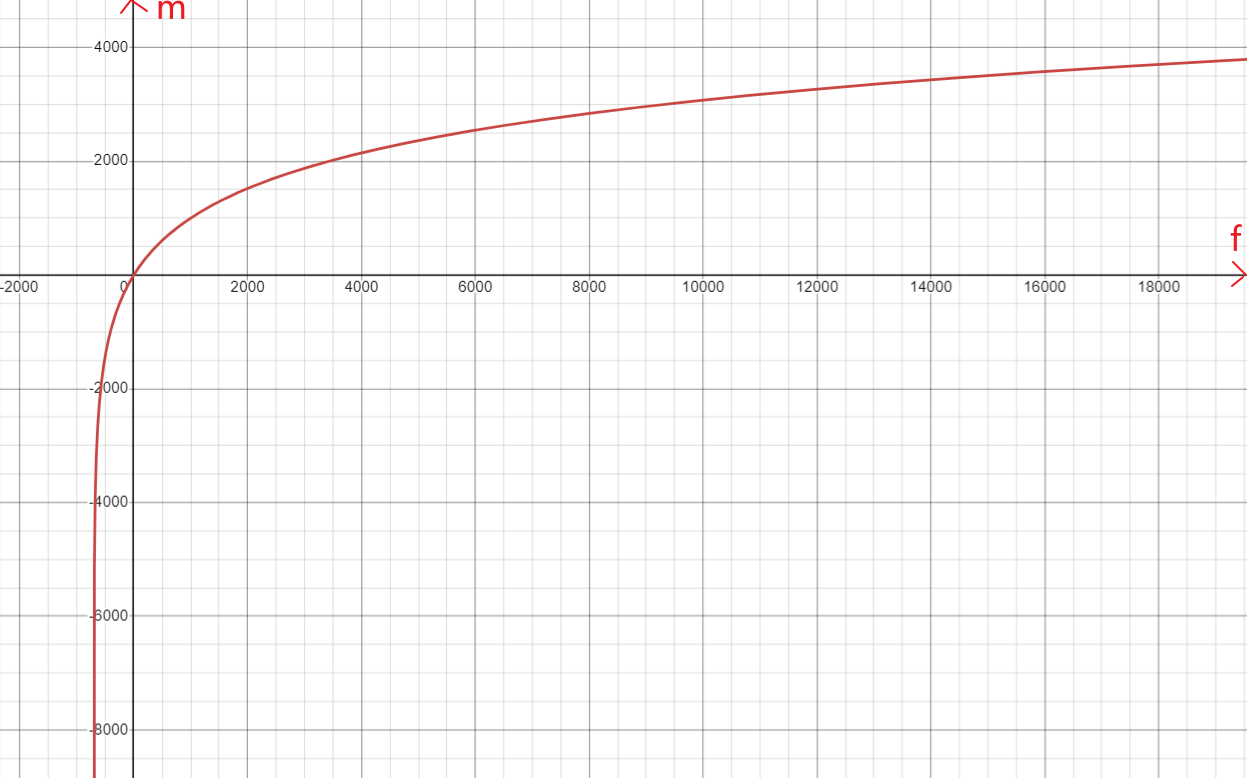
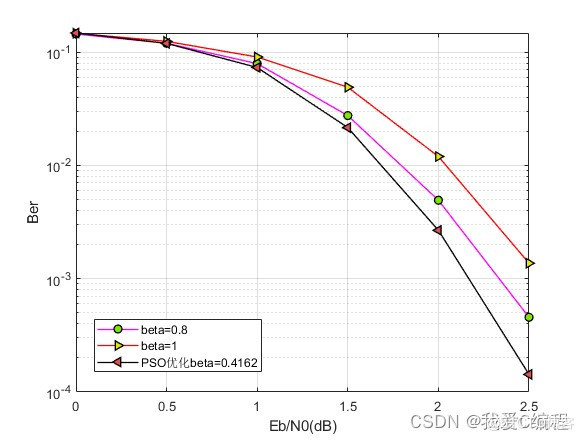
1.算法仿真效果
matlab2022a仿真结果如下:

2.算法涉及理论知识概要
Offset Min-Sum(OMS)译码算法是LDPC码的一种低复杂度迭代解码方法,它通过引入偏移量来减轻最小和算法中的量化效应,从而提高解码性能。当应用粒子群优化(PSO)来计算OMS译码算法中的最优偏移参数时,目标是自动找到能够最大化解码性能(如最小化误码率)的偏移量值。
PSO算法由粒子群、个体最优解(pBest)和全局最优解(gBest)三部分组成。每个粒子代表一个可能的解(在这里是归一化参数),通过迭代更新自己的位置(即解码参数)来逼近全局最优解。粒子的位置xi和速度vi在每一代(迭代)中按如下公式更新:
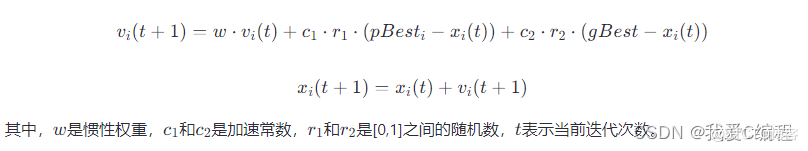
PSO应用于OMS偏移参数优化
初始化:随机生成一组粒子,每个粒子代表一个偏移参数γ的初始值,通常在合理范围内,如([-1, 1])。
适应度函数:定义适应度函数,通常为误码率(BER),越低的BER意味着更高的适应度值。
迭代优化:通过PSO的迭代过程,根据粒子在不同γ值下的解码性能(适应度),不断调整粒子的位置(即偏移量值),直至找到使BER最小化的最优γ。
3.MATLAB核心程序
for i=1:Iterifor j=1:Npeopif func_obj(x1(j,:))<pbest1(j)p1(j,:) = x1(j,:);%变量pbest1(j) = func_obj(x1(j,:));endif pbest1(j)<gbest1g1 = p1(j,:);%变量gbest1 = pbest1(j);endv1(j,:) = Wmax*v1(j,:)+c1*rand*(p1(j,:)-x1(j,:))+c2*rand*(g1-x1(j,:));x1(j,:) = x1(j,:)+v1(j,:); for k=1:dimsif x1(j,k) >= Xmaxx1(j,k) = Xmax;endif x1(j,k) <= Xminx1(j,k) = Xmin;endendfor k=1:dimsif v1(j,k) >= Vmaxv1(j,k) = Vmax;endif v1(j,k) <= Vminv1(j,k) = Vmin;endendendError2(i)=gbest1
end
figure
plot(Error2,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');
legend('Average fitness');bb = g1;
N = 2016;
K = 1008;
R = K/N;
%H矩阵
[ H, Hp, Hs ] = func_H();SNR = 0:0.5:3;
Ber = zeros(1, length(SNR));
Fer = zeros(1, length(SNR));%译码迭代次数
Iters = 8;
.................................................................
fitness=mean(Ber);figure
semilogy(SNR, Ber,'-b^',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.2,0.9,0.5]);xlabel('Eb/N0(dB)');
ylabel('Ber');
title(['OMS,GA优化后的alpha = ',num2str(bb)])
grid on;
save OMS3.mat SNR Ber Error2 bb
0X_058m