- 定点数表示
- 浮点数表示
- 习题
- 浮点数的规格化
- 例题
- 习题
计算机基础知识之原码、补码、反码和移码:https://www.cnblogs.com/kohler21/p/18233912
定点数表示
定点小数(纯小数)在计算机中的表示形式:
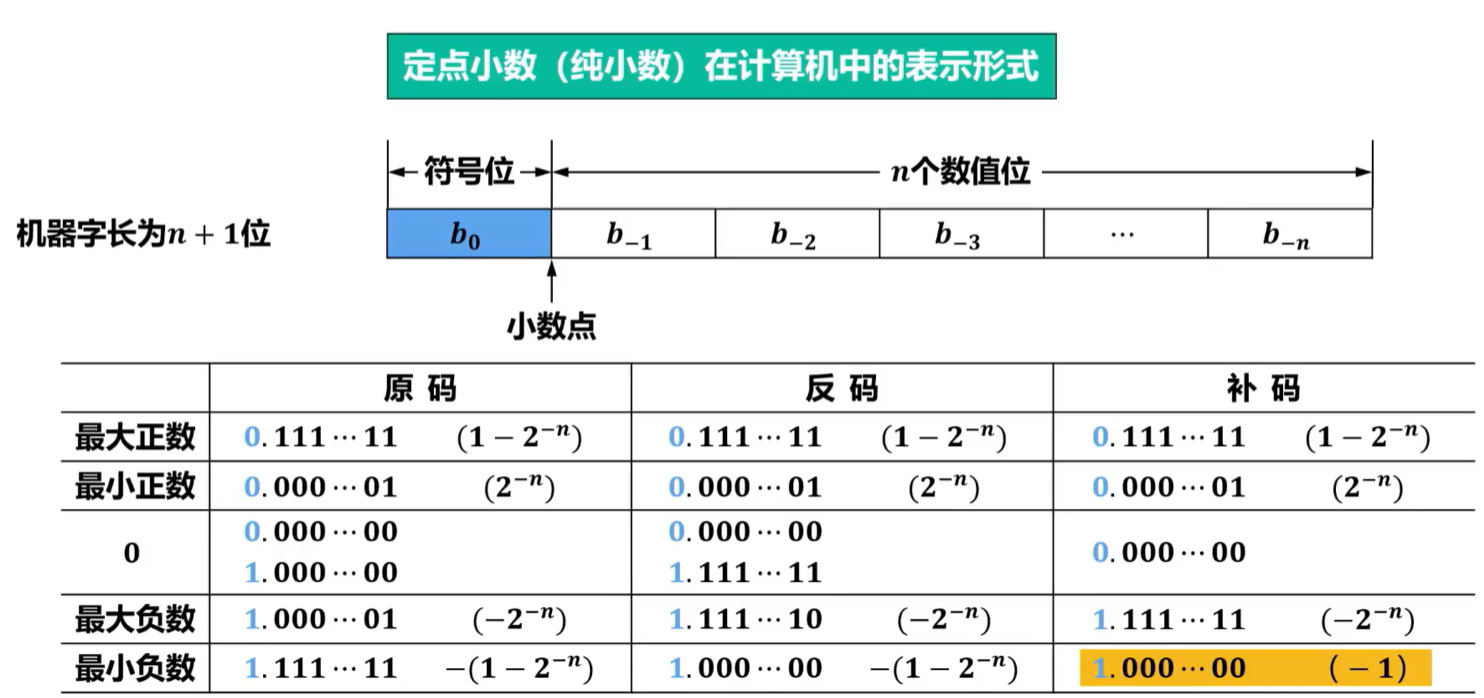
注:在计算机中,定点小数主要用于表示浮点数的尾数,并没有高级语言数据类型与之相对应。
定点整数在计算机中的表示形式:
注:在C语言中,char、short、int、long型都属于定点整数。
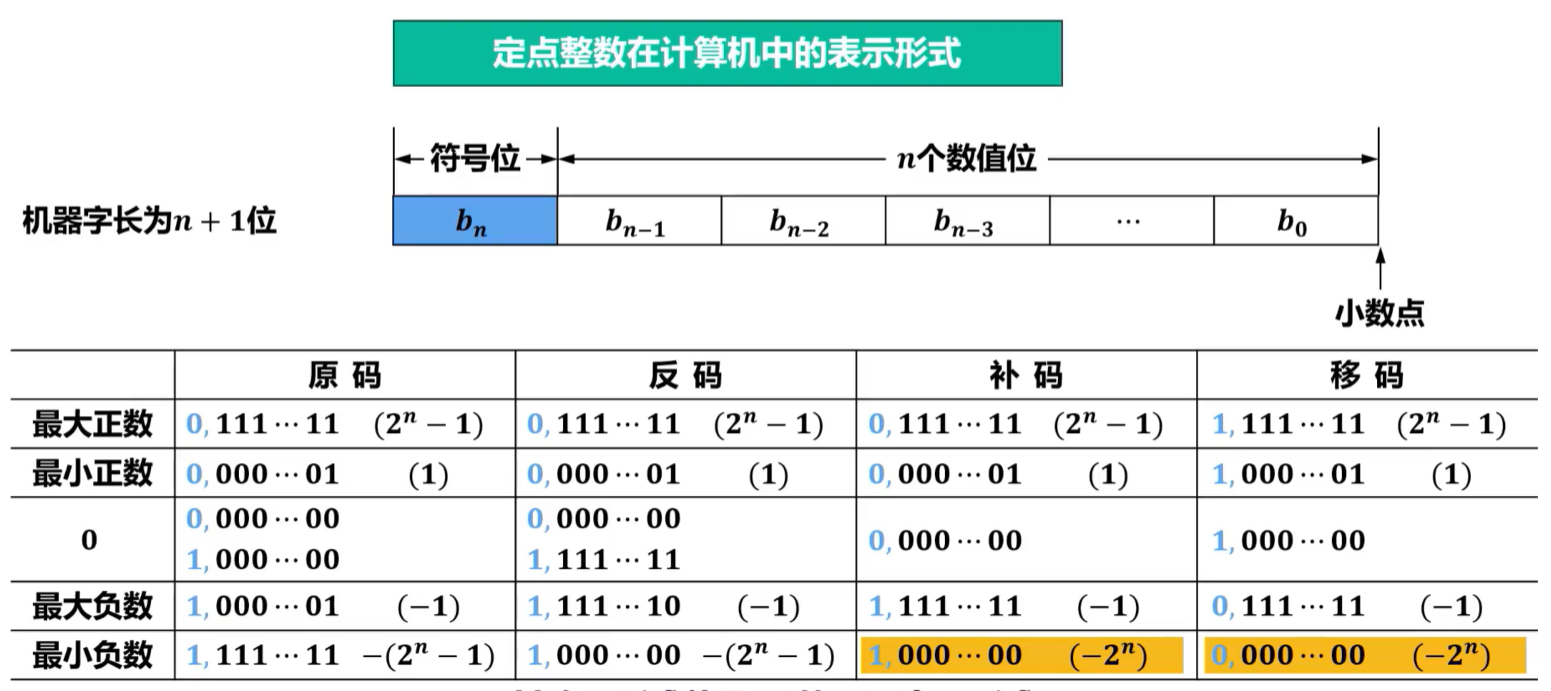
定点数所能表示的数据范围与下列因素有关。
- 机器字长:字长越长,其表示的数据范围就越大。
- 所采用的机器码:补码和移码所能表示的数据范围,比原码和反码所能表示的数据范围要多一个最小负数。
实际上,计算机中处理的数不一定都是纯小数或纯整数(例如圆周率3.1415926)。因此,这样的数不能直接用定点小数或定点整数表示。
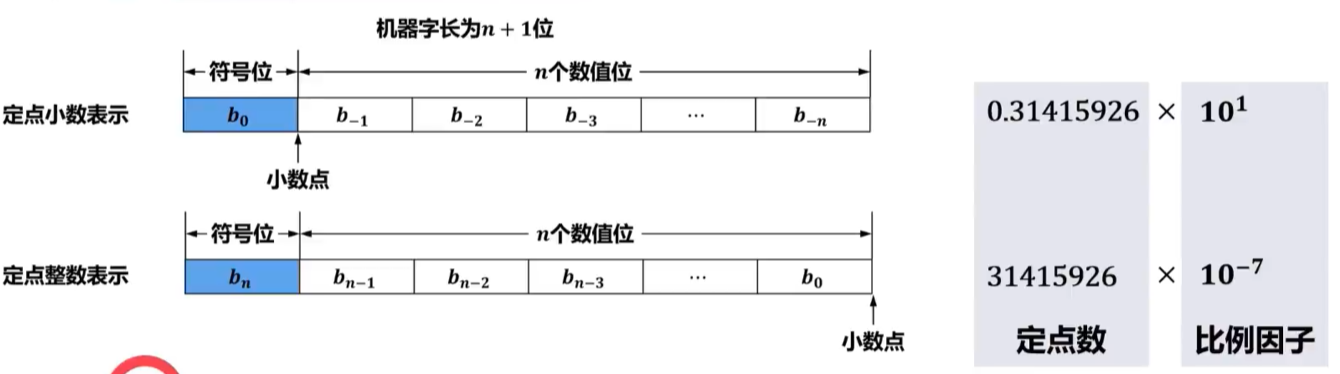
希望将浮点数直接表示在寄存器中:小数点的位置由寄存器中指定数位的内容给出;正负号由寄存器中指定数位的内容给出。
二进制浮点数可采用类似十进制科学记数法的表示方法。
十进制浮点数的表示:
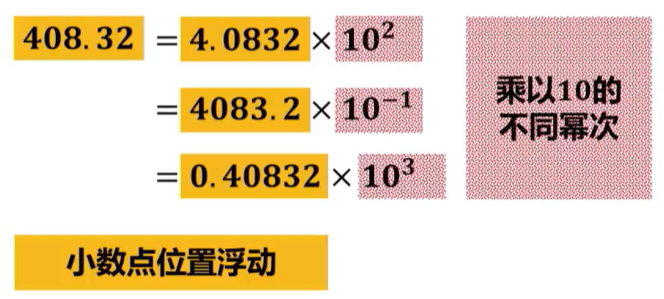

进而推广到二进制:
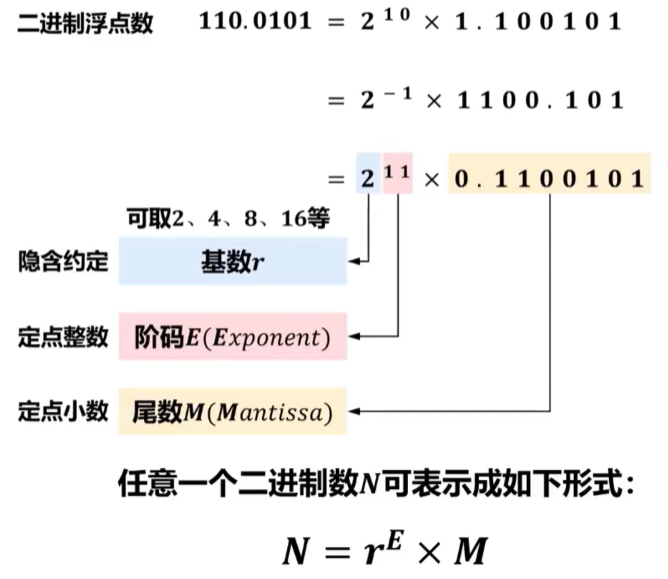
浮点数表示
进而得出浮点数在机器中的表示形式:
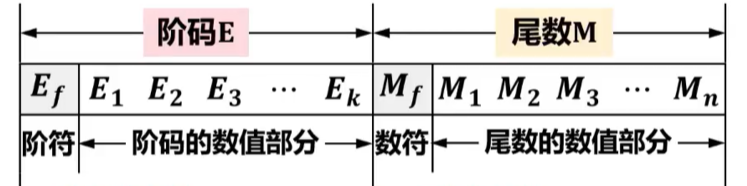
- 阶码的位数决定了数据表示的范围,位数越多,能表示的数据范围就越大。
- 阶码的值决定了小数点的位置。
- 尾数的位数决定了数据的表示精度。阶码长度相同时,分配给尾数的位数越多,数据表示的精度就越高。
- 阶码可采用原码、补码、反码、移码进行表示。
- 尾数可采用原码、补码、反码进行表示。
- 对应的浮点数表示范围会略有不同。
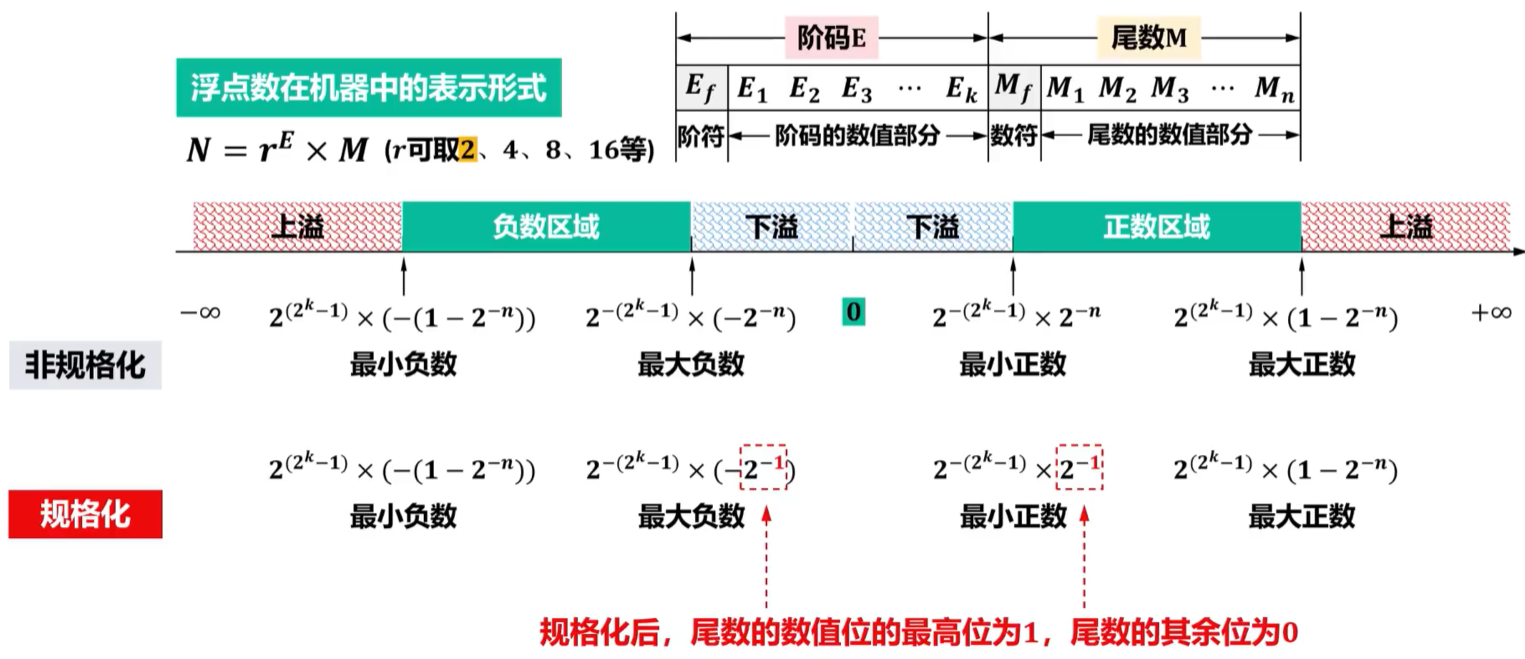
浮点数在机器中额度表示形式:N = \(r^{E}\) X M(r可取2、4、8、16等)。
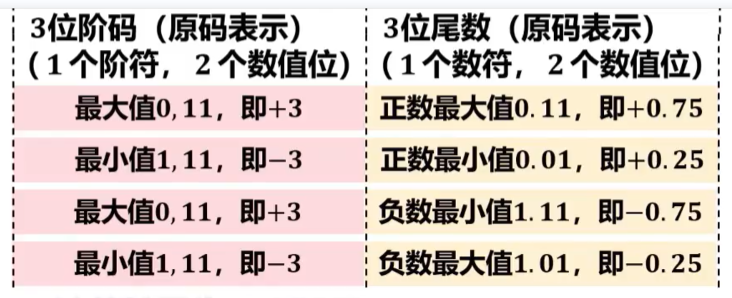

【练习】
(1)设浮点数字长为8位,其中阶码3位(含1位阶符),尾数5位(含1位数符),阶码和尾数均以原码表示,基数r为8,则浮点数的最大最小值分别是多少?
(2)设定点数原码为8位,则定点数的最大最小值分别是多少?(3)比较(1)和(2)能得出什么结论?

由此看见浮点数有效地扩大了数据的表示范围。
尽管浮点数有效扩大了数据表示范围,但受机器字长限制,浮点数仍然存在溢出现象。
- 当浮点数的阶码大于最大阶码时,称为上溢,此时机器停止运算,浮点运算器件会显示溢出标志。
- 当浮点数的阶码小于最小阶码时,称为下溢,虽然此时数据不能被精确表示,但由于发生下溢时数据的绝对值很小,通常将尾数各位强置为0,按机器0处理,此时机器可以继续运行。
- 当一个浮点数在正、负数区域中但并不在某个数轴刻度上时,也会出现精度溢出的问题,此时只能用近似数表示。

习题
【习题1】在浮点数的机器码(即机器数)表示中,不在机器码中出现(即隐含)的是(A)。
A.基数r
B.阶码E
C.尾数M
D.符号f
【习题2】假设浮点数A和B的字长相同, A的阶码位数大于B的阶码位数, A的尾数位数小于B的位数位数,其他规定都相同,则A和B可表示的数的范围和精度是(C )。
A. B可表示的数的范围大且精度高
B. A和B可表示的数的范围和精度相同
C. A可表示的数的范围大但精度低
D. A可表示的数的范围大且精度高
解析:阶码位数越大表示的数的范围越大,尾数位数越大则表示的数的精度越高。
【习题3】某浮点数字长为12位,其中阶码4位(含1位阶符号),基数为2,尾数8位(含1位数符),若阶码和
尾数都用补码表示,则该浮点数所能表示的最大正数是(D)。
A. \(2^{8}\)
B. \(2^{8}\) - 1
C. \(2^{7}\)
D.\(2^{7}\)-1
解析: 参考上方数轴中的最大正数的表示。
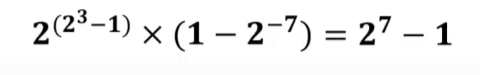
浮点数的规格化
根据浮点数的表示这一小节会发现存在一个问题:同一浮点数可能存在多种表示形式,也就是会有不同的阶码和尾数的组合。
举例如下:

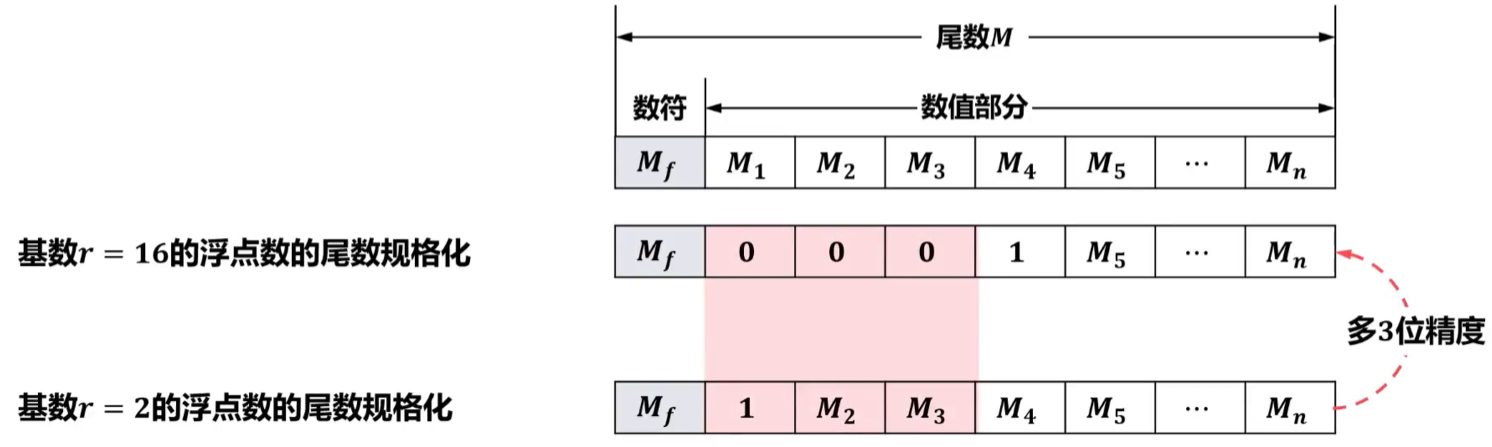
浮点数的规格化通常要求浮点数在数据表示时对尾数进行规格化处理,即使得尾数的最高数值位必须是一个有效值(尾数的数值部分的最高位为1)。在上述例子中只有第一种是符合规格化要求的。
浮点数规格化带来以下好处:
- 使浮点数的表示形式唯一。
- 使浮点数的表示精度最高。若数值部分的最高为0,则实际上该位对数值的表达是没有作用的。因为在构成数值时,该位的位权是没有作用的。而规格化就是要移除尾数数值部分最高位的0,这相当于数值部分能够补充相应数量的低位进而提高了表示精度。
对于非规格化尾数,需要对其进行规格化操作,即根据具体形式通过将非规格化尾数的数值部分进行左移或右移,并相应减少或增加阶码值的操作进行规格化,对应的规格化方法分别称为向左规格化(简称左规)和向右规格化(简称右规)。
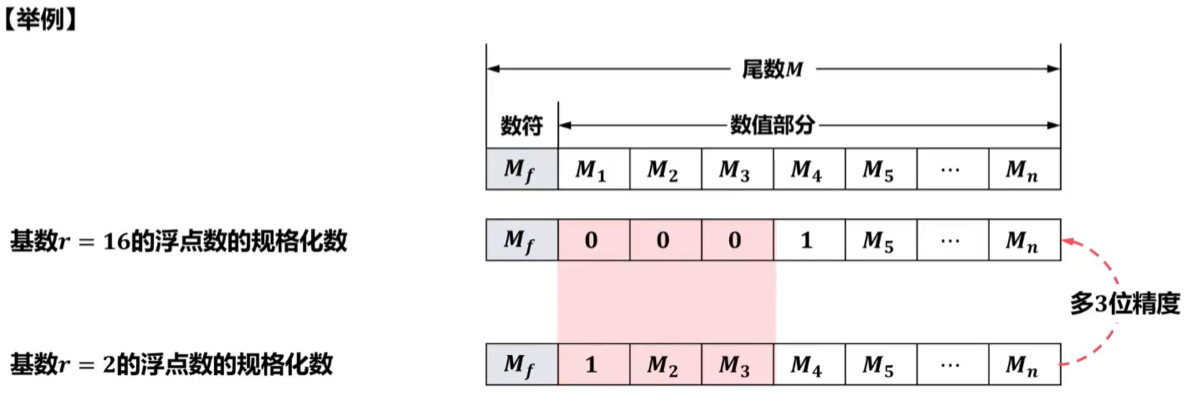
对于基数r不同的浮点数,因其规格化数的形式不同,规格化过程也不同。
-
当r=2时,尾数数值部分最高位为1的数为规格化数。
-
左规:尾数数值部分每左移1位,阶码减1。

-
右规:尾数数值部分每右移1位,阶码加1。
-
-
当r=4时,尾数数值部分最高2位不全为0的数为规格化数。
- 左规:尾数数值部分每左移2位,阶码减1。

- 右规:尾数数值部分每右移2位,阶码加1。
类比同上。
-
当r=8时,尾数数值部分最高3位不全为0的数为规格化数。
- 左规:尾数数值部分每左移3位,阶码减1。
- 右规:尾数数值部分每右移3位,阶码加1
依此类推,不难得到基数r为16或\(2^{n}\)时的规格化过程。
基数r不同,对数的表示范围和精度等都有影响。一般来说:基数r越大,可表示的浮点数范围越大,而且所表示的数的个数越多。但浮点数的精度反而下降。
浮点数规格化后的表示范围:
例题
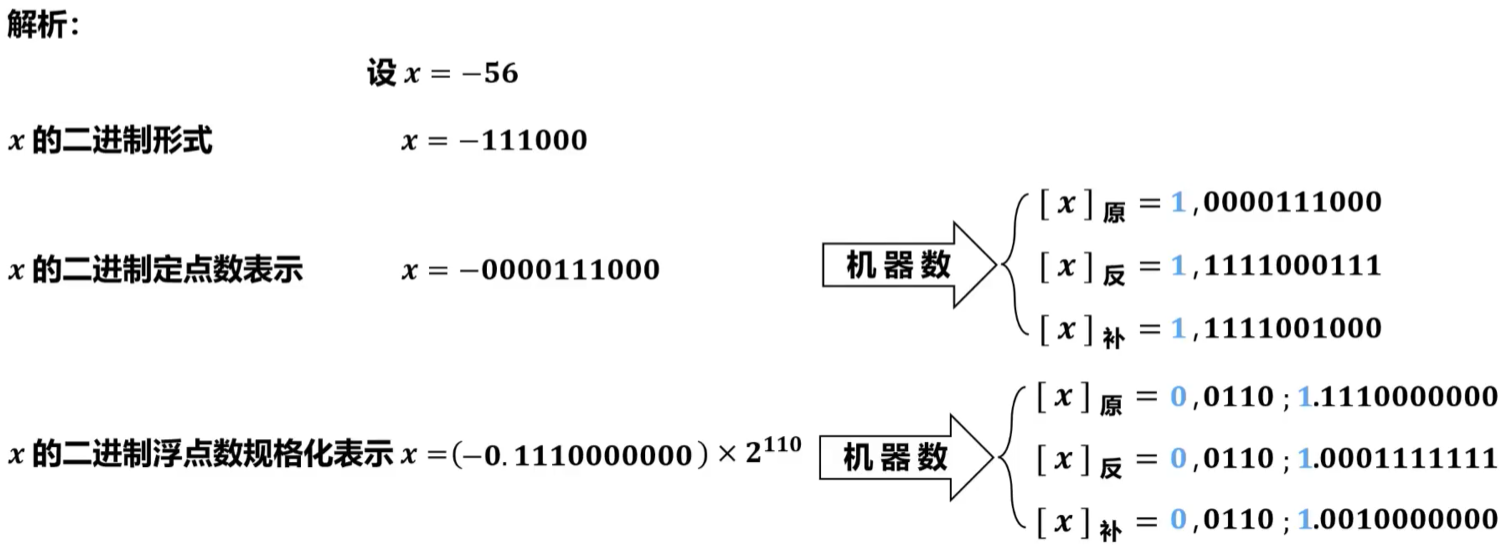
【例题1】设浮点数字长为16位,其中阶码5位(含1位阶符),尾数11位(含1位数符),将十进制数-56写成二进制定点数和浮点数(要求规格化表示),并分别写出它们各自的机器数(原码、反码、补码)形式。
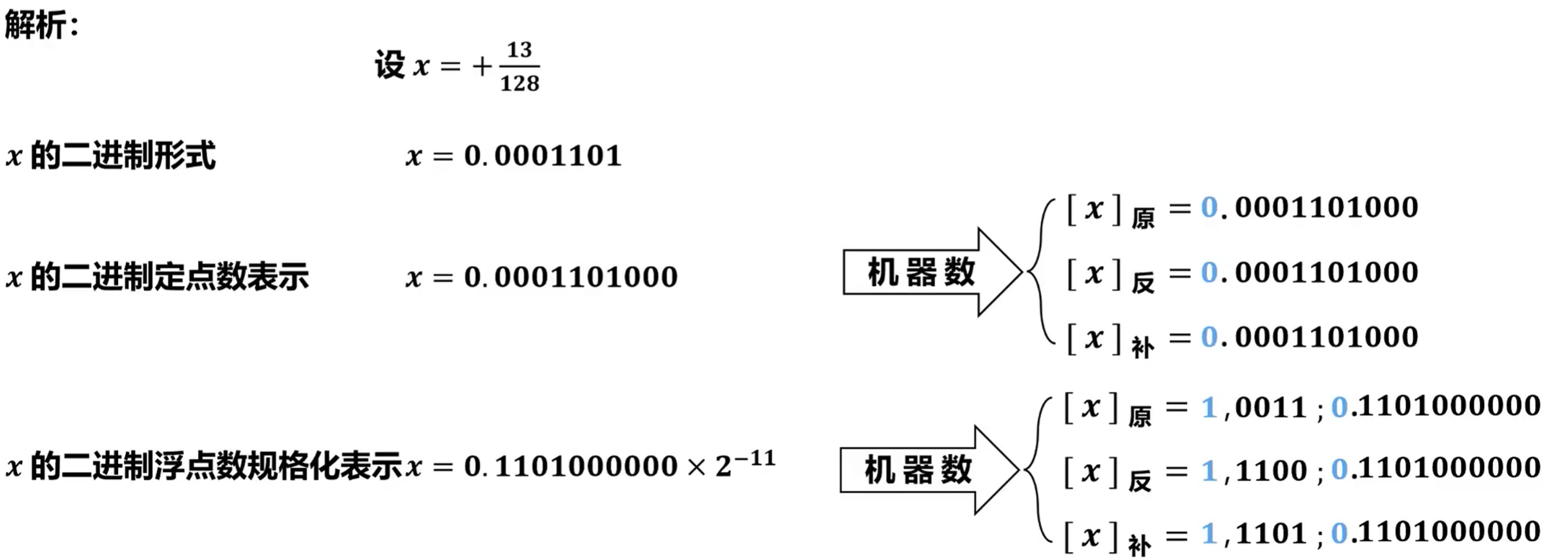
【例题2】设浮点数字长为16位,其中阶码5位(含1位阶符),尾数11位(含1位数符),将十进制数+\(\frac {13}{128}\)写成二进制定点数和浮点数(要求规格化表示),并写出它们各自的机器数(原码、反码、补码)形式。
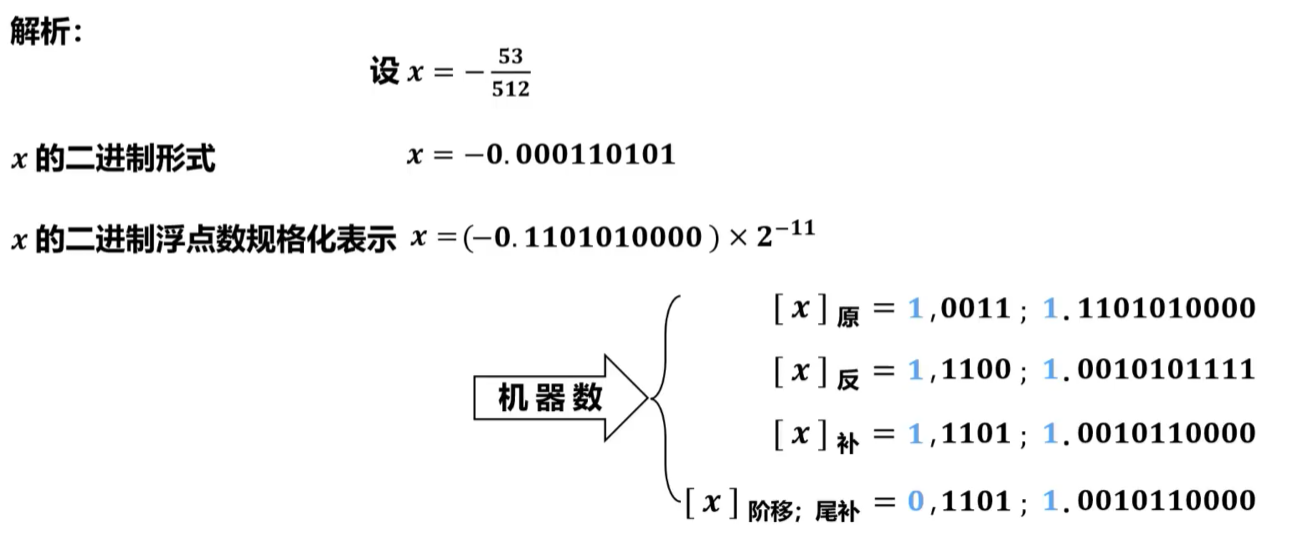
【例题3】设浮点数字长为16位,其中阶码5位(含1位阶符),尾数11位(含1位数符),写出十进制数-\(\frac {53}{512}\)对应的浮点规格化数的原码、反码和补码以及阶码用移码、尾数用补码的形式。
习题
【习题1】浮点数规格化带来的主要好处是( D)
A.方便浮点运算
B. 防止运算时数据溢出
C.增加数据的表示范围
D.增加数据的表示精度
解析:浮点数规格化带来以下好处:
- 使浮点数的表示形式唯一。
- 使浮点数的表示精度最高。
【习题2】假设浮点数A和B的字长、格式都相同,A的基数大于B,其他规定都相同,则A和B可表示的数的范围和精度是(C)。
A. B可表示的数的范围大且精度高
B. A和B可表示的数的范围和精度相同
C. A可表示的数的范围大但精度低
D. A可表示的数的范围大且精度高
解析:基数r不同,对数的表示范围和精度等都有影响。一般来说:基数r越大,可表示的浮点数范围越大,而且所表示的数的个数越多。但浮点数的精度反而下降。
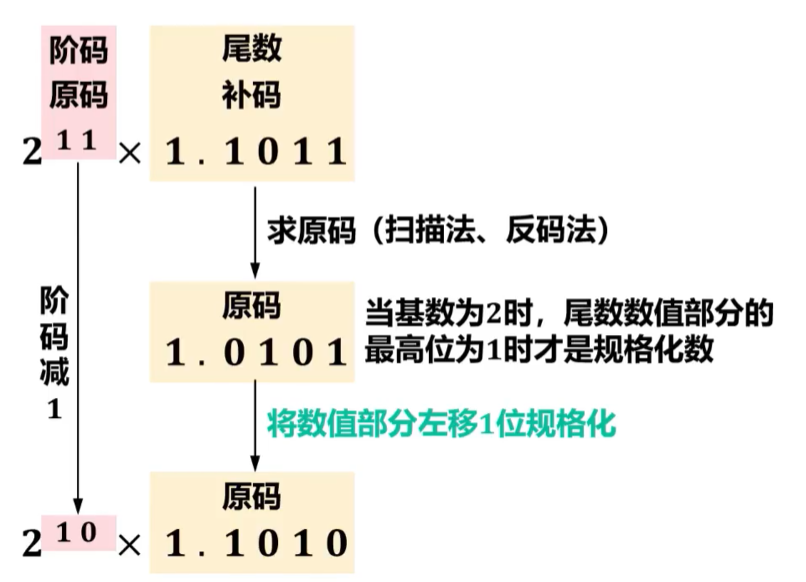
【习题3】若某浮点数为\(2^{11}\)×1.1011,其中阶码为原码表示,尾数为补码表示,则该浮点数(C)。
A.需要将尾数数值部分右移1位规格化
B.需要将尾数数值部分右移2位规格化
C.需要将尾数数值部分左移1位规格化
D.已经规格化
【习题4】假设浮点数的基数为8,尾数用原码表示,则以下尾数为规格化数的是(B)
A. 1. 0001001
B. 1. 0010111
C. 0. 0001001
D. 0. 0000111
解析:当r=8时,尾数数值部分最高3位不全为0的数为规格化数。

推荐阅读:
- 计算机基础知识之原码、补码、反码和移码
欢迎关注公众号:愚生浅末