本文将探讨了缺失值插补的不同方法,并比较了它们在复原数据真实分布方面的效果,处理插补是一个不确定性的问题,尤其是在样本量较小或数据复杂性高时的挑战,应选择能够适应数据分布变化并准确插补缺失值的方法。
我们假设存在一个潜在的分布P,从中得出观察值X。此外,还绘制了一个与X相同维数的0/1向量,我们称这个向量为M,实际观测到的数据向量X被M掩码为X。我们观测到联合向量(X,M)的n个独立同分布(i.i.d)副本。如果我们把它写成一个数据矩阵,它可能看起来像这样:
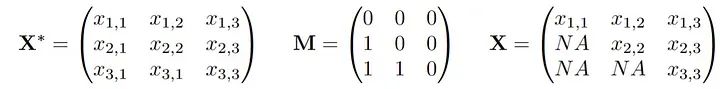
较小的x,m表示“观察到的”,而较大的值则表示随机数量。大家讨论的缺失机制就是对(X*,M)的关系或联合分布的假设:
完全随机缺失(MCAR):一个值丢失的概率就像抛硬币一样,与数据集中的任何变量无关。缺失值只是一件麻烦事。你可以忽略它们,只关注数据集中完全观察到的部分,这样就不会有偏差。在数学中,对于所有m和x:
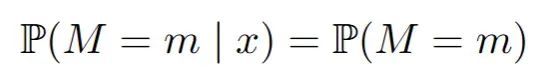
随机缺失(MAR):缺失的概率现在可以依赖于数据集中观察到的变量。一个典型的例子是两个变量,比如收入和年龄,其中年龄总是被观察到,但收入可能会因为年龄的某些值而丢失。这可能听起来很合理,但这里可能会变得复杂。在数学中,对于所有m和x:
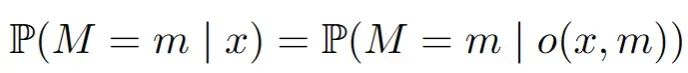
非随机缺失(MNAR):这里一切皆有可能,我们不能笼统地概括。但是最终我们需要学习给定一个模式m '中观测值的缺失值的条件分布,以便在另一个模式m中推算。
实现这一点的著名的方法称为链式方程多重插补(Multiple Imputation by Chained Equations, MICE):首先使用简单的插补方法填充值,例如均值插补。然后对于每一次迭代t,对每一个变量j,根据所有其他已插补的变量进行回归分析(这些变量已被插补)。然后将这些变量的值填入已学习的插补器中,用于所有未观察到的X_j。在R语言中,可以方便地使用mice包来实现。我这种方法在实际应用中效果非常好,MICE中重现某些实例的底层分布的能力非常惊人。我们下面会用一个非常简单的例子(只有一个变量缺失,因此我们可以手动编码),模拟MICE通常会迭代执行的过程,以更好地了解他的工作原理。
https://avoid.overfit.cn/post/9f66c5f8cd204ed685af0744b935ddd5
![[TinyRenderer] Chapter1 p1 Output Image](https://img2023.cnblogs.com/blog/3326624/202406/3326624-20240610113043187-1789112514.bmp)







![[linux]mark-tool](https://img2024.cnblogs.com/blog/1237275/202406/1237275-20240610105607238-1261637242.png)