原题链接:https://www.luogu.com.cn/problem/P5017
题意解读:先将问题进行抽象、建模。
设一条数轴,从左到右,每个点对应一个时刻,每个时刻可能有多个人到达,然后有若干个发车时刻,每两个发车时刻间隔必须>=m,每个人的等待时长就是到最近一个发车时刻的时间累加,计算所有人等待时间最小值。
对样例2进行模拟:

1时刻1人出发,等待0;6时刻两人出发,等待2;14时刻两人出发,等待2;总等待时长4,没有比4更小的等待时长。
解题思路:
如何来求解最小的等待时长?
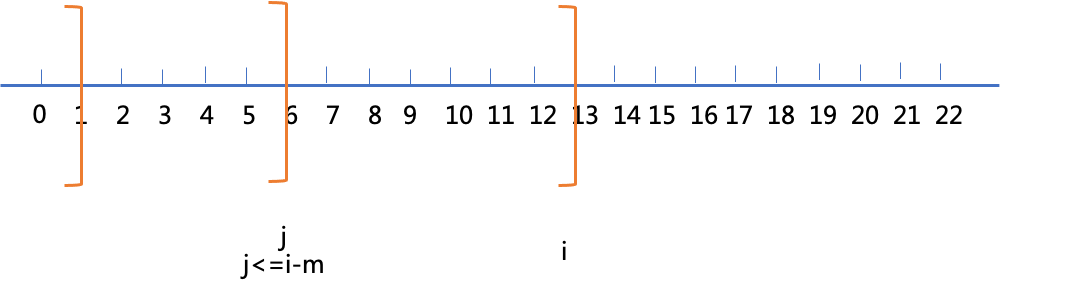
设f[i]表示前i个时刻,最后在i时刻有发车时,所有人的最小等待时长。
那么考虑上一个发车时刻j,我知道i - j >= m,所以j <= i - m
得到递推关系:f[i] = min{f[j] + (j,i]之间所有人到i的时间之和}
(j,i]之间所有人到i的时间之和如何计算:
设cnt[i]表示前i时刻到达的人数,sum[i]表示前i时刻所有到达人的时刻之和,则有
(j,i]之间所有人到i的时间之和 = (cnt[i] - cnt[j]) * i - (sum[i] - sum[j])
所以,f[i] = min{f[j] + (cnt[i] - cnt[j]) * i - (sum[i] - sum[j])},j <= i - m
还要考虑i < m的情况,f[i] = cnt[i] * i - sum[i]
此时:整体时间复杂度是n^2,n是时刻最大值,在4000000,总体复杂度会超时,需要进行优化。
优化一:减少冗余状态
如果i时刻前m时间之内没有一个人,那么f[i]就不用通过递推算了,直接f[i] = f[i-m],判断条件是cnt[i] == cnt[i-m]
优化二:减少转移范围
当前j<=i-m,而如果j <= i-2m,即j到i之间车可以有两个往返,那么车必然可以增加一次发车,这样能带更多的人,所以j最好>i-2m且<=i-m
结果:f[最后一个达到的人的时刻] ~ f[最后一个达到的人的时刻+m]的最小值
100分代码:
#include <bits/stdc++.h>
using namespace std;const int N = 4000105;
int n, m, t, maxt;
int cnt[N], sum[N]; //设cnt[i]表示前i时刻到达的人数,sum[i]表示前i时刻所有到达人的时刻之和
int f[N]; //f[i]表示前i个时刻,最后在i时刻有发车时,所有人的最小等待时长。
int ans = INT_MAX;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++){cin >> t;maxt = max(maxt, t);cnt[t]++, sum[t] += t;}//最后一个同学可能等到的时间maxt + m - 1for(int i = 1; i < maxt + m; i++){cnt[i] += cnt[i - 1];sum[i] += sum[i - 1];}memset(f, 0x3f, sizeof(f));for(int i = 0; i < maxt + m; i++){if(i >= m && cnt[i] == cnt[i - m]){f[i] = f[i - m];continue;}if(i < m)f[i] = cnt[i] * i - sum[i]; elsefor(int j = max(0, i - 2 * m + 1); j <= i - m; j++){f[i] = min(f[i], f[j] + (cnt[i] - cnt[j]) * i - (sum[i] - sum[j]));}}for(int i = maxt; i < maxt + m; i++) ans = min(ans, f[i]);cout << ans;return 0;
}