重点
- 贝叶斯信念
- 信息搜寻预期收益(大题)
课程内容
了解信息决策的基本原理,重点掌握信息搜寻理论的分析框架及其在具体实践中的应用。
§ (1)信息与一般决策过程
§ (2)不确定性与信息离散分布
§ (3)信息搜索模型
§ (4)最优信息决策
信息与决策
nothing important
- 客观信息与主观信息(信念)
- 完全信息与不完全信息
- 公共信息与私人信息
- 决策树与条件期望
最优信息决策理论
理论模型
行动空间(Action):\(\Omega = \{ 1,2,\dots, x \}\)
状态空间(State):是隐藏未知的,相当于上一章的不确定性\(\mathcal{S} = \{ 1,2,\dots, s \}\)
信念:代表状态出现的概率,\(\pi : \mathcal{S} \to \mathbb{R}\)
在上述描述一下,决策准则即采取行动使得期望收益/效用最大化

在获取消息之后,会更新信念,然后再次进行决策
上述过程叫做贝叶斯信念修正
- 贝叶斯信念修正的隐含命题:
- 先验概率的大小决定了“消息”的价值空间,在主观确定性事件中,信息价值为零;
- 消息越丰富,消息对主观价值的修正越大,后验分布产生“变异”的可能性越大;
- 小概率消息,或称奇异消息(消息初始概率 qm 较小的消息)更能造成信念修正,符合主观上人们的猎奇心态和细节的关注。
信息价值
即信念更新之后的期望收益的差值
信息搜索模型
价格离散
定义:同质商品在市场中价格不同的现象
-
价格离散的原因
- 价格在一定市场中的波动,难以观测到准确的市场价格,存在讨价还价的空间
- 信息不对称
- 信息老化
- 市场经营和销售条件差别
- 商品异质性
- 价格在一定市场中的波动,难以观测到准确的市场价格,存在讨价还价的空间
-
价格离散的影响
- 获得价格离散程度和波动的知识成为有利可图,出现一批从事信息搜集和分析的服务机构,信息服务机构应运而生
-
价格离散的经济意义
- 市场信息的不完备性,对市场了解的人成为市场代理人或信息服务提供商;
- 信息搜集行为
- 诱发和刺激了信息搜索行动
信息搜寻理论
经济学家认为,信息是人们做出决策的基础。信息是有代价的,获得信息要付出金钱与时间,这就是寻找信息的成本,称为信息搜寻成本。
信息也会带来收益,有更充分的信息可以做出更正确的决策,这种决策会使经济活动的收益更大,这就是信息搜寻收益
信息搜寻预期收益
随着搜寻次数的增加,期望收益会逐渐增加,但是增加的幅度会逐渐减小,最终会收敛到一个值
而搜寻成本是一个递增的函数,因此最优的搜寻次数是使得搜寻收益减去搜寻成本最大的次数
例题看最后
工作搜索模型
pass
信息搜寻与决策案例分析
pass
例题
贝叶斯信念更新

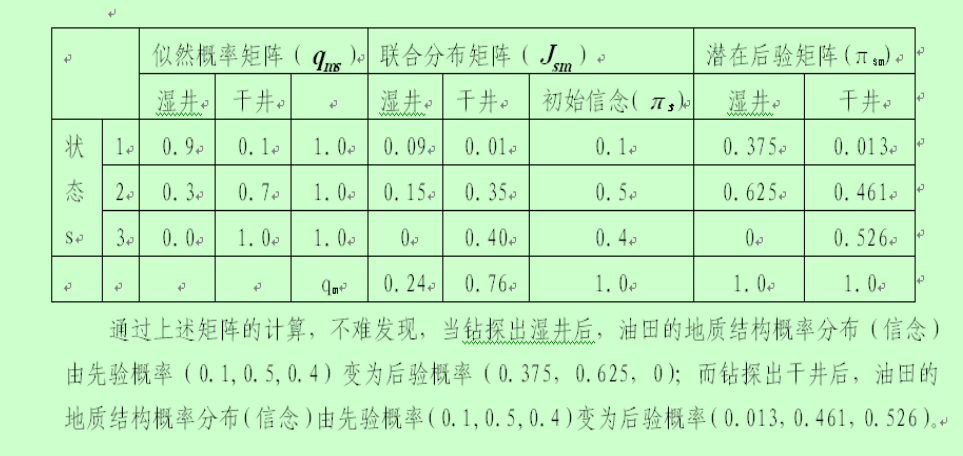
信息价值

信息搜寻预期收益
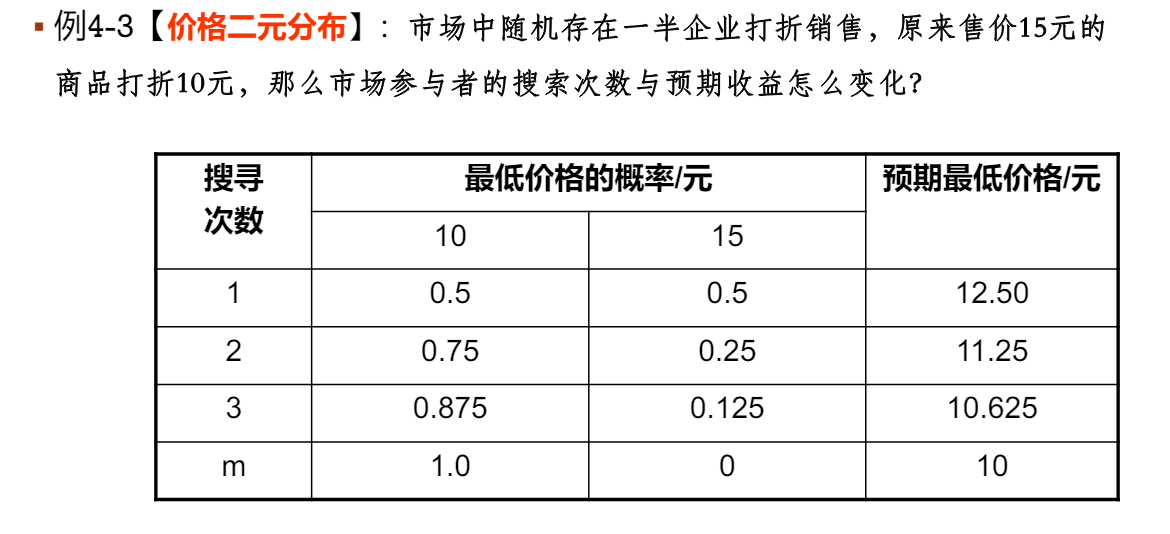
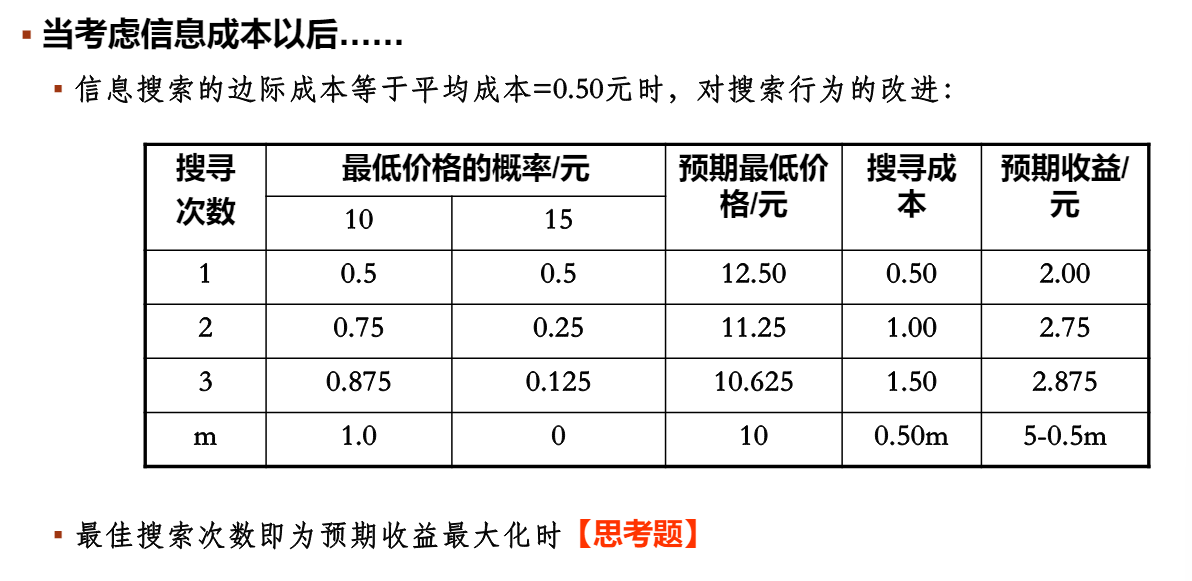
收益最大的时候即为,搜寻的边际收益=搜寻的边际成本时