状压dp
1.状态压缩
状态压缩就是使用某种方法,以最小的代价来表示某种状态,通常是用一串01数字(二进制数)来表示各个点的状态。这就要使用状态压缩的对象的点的状态只有两种:0和1。
2.使用条件
1.解法需要保存一定的状态数据(表示一种状态的一个数据值),每个状态通常情况下是可以用二进制来表示的。这就要求状态数据的每个单元只有两种状态,比如棋盘上的格子放或不放棋子。
2.解法需要将状态数据实现为一个基本数据类型,比如int,longlong等,即所谓的状态压缩。状态压缩的目的一方面是缩小了数据存储的空间,另一方面是在状态比对和状态整体处理时能够提高效率。这就要求状态数据中的单元个数不能太大,比如用int来表示一个状态的时候,状态的单元个数不能超过32,所以题目一般都是至少有一维的数据范围很小。
3.状压dp
动态规划问题通常有两种,一种是对递归问题的记忆化求解,另一种是把大问题看作是多阶段的决策求解。这里用的便是后一种,这带来一个需求,就是存储之前的状态,再有状态及状态对应的值推演出状态转移方程最终得到最优解。
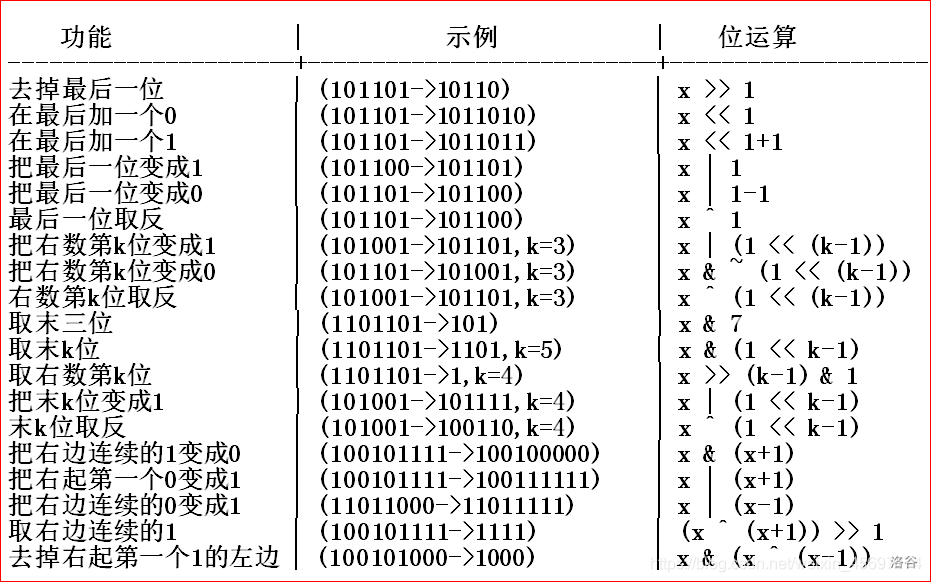
4.位运算
一般基础的状压就是将一行的状态压成一个数,这个数的二进制形式反映了这一行的情况。由于使用二进制数来保存被压缩的状态,所以要用到二进制位运算操作,将一个十进制数转成二进制进行位运算操作再转回十进制数。
引例:状态压缩dp
题目描述:
在\(n \times n (n \le 20)\)的方格棋盘上放置n个车,求使他们不能互相攻击的总方案数。
解析:
解法1:组合数学
第一行有n种选择,第二行有n-1种选择\(\cdots\)根据乘法原理,答案是n!。
解法2:状压递推
取棋子的放置情况作为状态,某一列如果已经放置棋子则为1,否则为0.这样,一个状态就可以用一个最多20位的二进制数表示。
例如\(n=5\),第1、3、4列已经放置,则这个状态可以表示为01101(从右到左)。设\(f_s\)为达到状态s的方案数,则可以尝试建立f的递推关系。
考虑\(n=5\),\(s=01101\)
因为我们是一行一行放置的,所以当到达s时已经放到了第三行。又因为一行能且仅能放置一个车,所以我们知道状态s一定来自:
1.前两行在第3、4列放置了棋子,第三行在第1列放置;
2.前两行在第1、4列放置,第三行在第3列放置;
3.前两行在第1、3列放置,第三行在第4列放置。
根据加法原理,\(f(s)\)应该等于这三种情况的和,写成递推式是:
\(f(01101) = f(01100) + f(01001) + f(00101)\)
根据上面的讨论思路推广,得到解决办法:
\(f(0) = 1\),\(f(s) = f(s - 2^i)\)
其中s的右起第i+1位为1。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
ll dp[1100000];
ll n;
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;dp[0] = 1;for (rg int s = 1; s < (1 << n); s++) {for (rg int i = 0; i < n; i++) {if ((s >> i) & 1) dp[s] += dp[s - (1 << i)];}}cout << dp[(1 << n) - 1] << "\n";return qwq;
}
例题1:特殊方格棋盘
题目描述:
在\(n \times n(n \le 20)\)的方格棋盘上放置n个车,某些格子不能放,求使他们不能互相攻击的方案总数。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define lowbit(x) (x & -x)
using namespace std;
typedef long long ll;
const int N = 25;
int a[N];
ll f[(1 << 20) + 5];
int n, m;
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m;int ms = (1 << n) - 1;int x, y;for (rg int i = 1; i <= m; i++) {cin >> x >> y;a[x] = a[x] | (1 << (y - 1)); //把 a[x]中不能放车的位置置为 1 }f[0] = 1;for (rg int i = 1; i <= ms; i++) {rg int temp, num = 0;for (temp = i; temp; temp -= lowbit(temp)) { //挨个减掉 2的 k次幂 num++; //记录当前已经放了几辆车,放到第几行了 }temp = i & (~a[num]); //放到第 i行,i&不能放置为 0,temp为第 i个车能放在哪些列。temp二进制就是为了排除掉坑 while (temp) {f[i] += f[i ^ lowbit(temp)]; //只有 lowbit(temp)才是可以放的位置temp -= lowbit(temp);} }cout << f[ms] << "\n";return qwq;
}
例题2
题目描述:
有一个\(n \times m(n,m \le 80, n \times m \le 80)\)要在棋盘上放\(k(k \le 80)\)个棋子,使得任意两个棋子不相邻,且有些格子不能放,求和法的方案总数。
解析:
隐含条件:\(9 \times 9 = 81 > 80\),则n,m不可能同时大于9,因此\(min(n,m) \le 8\)。若\(m > n\),交换m和n;
每行的状态可以用m位的二进制表示,然后逐行放置。
行限制:每行可以放0到\(\frac m 2\)个棋子,只要棋子放定则第i行状态\(S_i\)便确定;
列限制:放第i行时需要与第i-1行比较,若\(S_i \& S_{i-1} = 0\)则该组合是可行的。对于确定的\(S_i\)需要枚举其对应的组合\(S_{i-1}\),然后采用加法原理相加,因此\(S_i\)应该设计到状态中去。
棋子放置个数不得超过k,因此放置棋子的个数也应该设计到状态中去。
状态设计:\(f[i][j][S_i]\)表示前i行共放置j个棋子,且第i行棋子状态为\(S_i\)时的方案数。
目标状态:\(f[n][k][\)所有满足条件的\(S]\)
状态转移:\(f[i][j][S_i] = \sum f[i-1][j-\)状态\(S_i\)中1的个数\(][S_{i-1}]\)
空间优化1:滚动数组,将维度i滚动掉
时间优化1:预处理(dfs或子集枚举)出满足行限制的状态集合S,并记录每个元素\(S_i\)中含有多少个1
空间优化2:预处理会去掉很多无用状态,可缩小第3维;将状态重新设计为\(f[i][j][k]\)表示前i行共放置j个棋子,且第i行棋子状态为\(S_k\)时的方案数。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
ll f[81][1 << 9][21];
inline int getnum(int x) { //判断 x的二进制中是否有两个连续的1,有输出-1,没有输出对应二进制数的1的位数 rg int last = 0, tmp = 0;while (x) {if (last && (x & 1)) return -1; //last存储上一位的检验 if (last == (x & 1)) tmp++; //last用来判断最后一位是不是1,是的话 tmp+1 x >>= 1;}return tmp;
}
int n, m, t;
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m >> t;if (n < m) swap(n, m);memset(f, 0, sizeof(f));f[0][0][0] = 1;for (rg int i = 1; i <= n; i++) {for (rg int r = 0; r <= t; r++) {for (rg int j = 0; j < (1 << m); j++) {rg int num = getnum(j);if (num == -1 || num > r) continue;for (rg int k = 0; k < (1 << m); k++) {if (getnum(k) == -1 || (k & j)) continue;f[i][j][r] += f[i - 1][k][r - num];}}}}ll ans = 0;for (rg int i = 0; i < (1 << m); i++) ans += f[n][i][t];cout << ans << "\n";return qwq;
}
例题3:互不侵犯
题目描述:
在\(n \times n\)的棋盘里放k个国王,使他们互不攻击,求共有多少种摆放方案。(国王能攻击到他上下左右以及左上左下右上右下共8个格子)。
解析:
状态设置:\(dp[i][j][S]\)表示我们已经选到了第i行,用了j个国王,第i行状态为S;
转移方程:\(dp[i][j][S_2] += dp[i-1][j-cnt[S_2]][S_1]\)
1.思考,如果第i-1行的的第j位是1,第i行的第j-1,j,j+1位一定为0。那么怎么表示呢?
(1)当j位置上为1时,\(S_1 \& S_2 \ne 0\);
(2)当j+1位置上为1时,\((S_2 << 1) \& S_1 \ne 0\);
(3)当j-1位置上为1时,\((S_2 >> 1) \& S_1 \ne 0\)
2.处理完行间限制,接下来处理行内限制:一个国王的左右两格不能再放国王了。
(1)当左边的格子为1时,\((S_2 >> 1) \& S_2 \ne 0\)
(2)当右边的格子为1时,\((S_2 << 1) \& S_2 \ne 0\)
因为第二个条件只与状态的情况有关,所以我们可以预处理这个东西,dp时将所有满足第二条性质的状态拿出来看看是否满足第一条性质就好了。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
ll cnt[2000], ok[2000]; //cnt[i]表示第 i种状态的二进制中有几个 1,ok[i]表示第 i行内不相矛盾
ll dp[10][100][2000];
int n, k, num;
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> k;for (rg int s = 0; s < (1 << n); s++) {rg int tot = 0, s1 = s;while (s1) {if (s1 & 1) tot++;s1 >>= 1;}cnt[s] = tot;if ((((s << 1) & s) == 0) && (((s >> 1) & s) == 0)) ok[++num] = s;//if ((((s << 1) | (s >> 1)) & s) == 0) ok[++num] = s; //更短的写法}dp[0][0][0] = 1;for (rg int i = 1; i <= n; i++) {for (rg int l = 1; l <= num; l++) { //枚举所有满足条件2的状态 rg int s1 = ok[l];for (rg int r = 1; r <= num; r++) {rg int s2 = ok[r];if (((s2 & s1) == 0) && (((s2 << 1) & s1) == 0) && (((s2 >> 1) & s1) == 0)) {//if (((s2 | (s2 << 1) | (s2 >> 1)) & s1) == 0) { //更短的写法for (rg int j = 0; j <= k; j++) {if (j - cnt[s1] >= 0) dp[i][j][s1] += dp[i - 1][j - cnt[s1]][s2];}} }}}ll ans = 0;for (rg int i = 1; i <= num; i++) {ans += dp[n][k][ok[i]];}cout << ans << "\n";return qwq;
}
例题4:炮兵阵地
题目描述:
一个\(N \times M\)的地图由N行M列组成,地图的每一格可能是山地(用H表示),也可能是平原(用P表示)。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队)。它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格(攻击范围不受地形的影响)。现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
int dp[105][1050][1050]; //dp[i][j][k]表示第i行状态为第j个可行状态,且上一行状态是第k个可行状态
int line[105]; //第i行的状态
int state[1050]; //第i个可行状态是多少
int need[1050]; //第i个可行状态中1的个数
int can[105][1050]; //第i行中第j个方案是否可行
int cnt;
int n, m;
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m;for (rg int i = 1; i <= n; i++) {char str[15];cin >> str;for (rg int j = 0; j < m; j++) {line[i] = (line[i] << 1) + (str[j] == 'P');}}for (rg int i = 0; i < (1 << m); i++) {if (((i << 1) & i) == 0 && ((i << 2) & i) == 0) {state[++cnt] = i; //第i个可行状态rg int t = i;while (t) {need[cnt] += (t & 1);t >>= 1;} }}for (rg int i = 1; i <= cnt; i++) { //第一行 if ((state[i] | line[1]) == line[1]) {can[1][i] = 1;dp[1][i][0] = need[i]; }}for (rg int i = 1; i <= cnt; i++) { //第二行 if ((state[i] | line[2]) == line[2]) {can[2][i] = 1;for (rg int j = 1; j <= cnt; j++) {if (!can[1][j]) continue;if ((state[i] & state[j]) == 0) { //上下两行的状态不能冲突 dp[2][i][j] = max(dp[2][i][j], dp[1][j][0] + need[i]);}}}}for (rg int i = 3; i <= n; i++) {for (rg int j = 1; j <= cnt; j++) {if ((state[j] | line[i]) == line[i]) {can[i][j] = 1;for (rg int k = 1; k <= cnt; k++) {if (!can[i - 1][k]) continue;if (state[j] & state[k]) continue; //上下不能相邻for (rg int g = 1; g <= cnt; g++) { //枚举上下两行状态 if (!can[i - 2][g]) continue;if ((state[j] & state[g]) || (state[k] & state[g])) continue;dp[i][j][k] = max(dp[i][j][k], dp[i - 1][k][g] + need[j]);} }}}}int ans = 0;for (rg int i = 1; i <= cnt; i++) {for (rg int j = 1; j <= cnt; j++) {ans = max(ans, dp[n][i][j]);}}cout << ans << "\n";return qwq;
}
例题5:集合选数
题目描述:
对于任意一个正整数n,求{1,2,…,n}的满足以下条件的子集的个数:若x在该子集中,则\(2x\)和\(3x\)不能在该子集中。结果对\(10^9+1\)取模。
解析:
一道构造题。要\(2x\)与\(3x\)都不在集合内不好处理,所以我们需要构造出一个与原命题等价的命题。
于是有:构造一个矩形,第一行第一列为1,第一行后面所有数均为前面数的两倍。接下来每列的数都是它上面的数的三倍。构造出来大概是这样:
1 2 4 8 16 32\(\cdots\)
3 6 12 24 48 96\(\cdots\)
9 18 36 72\(\cdots\)
那么对于这个矩形,我们要做的就是求出在矩形内选出一些数使得相邻的数不能选的方案数。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int mod = 1e9 + 1, maxn = (1 << 18) - 1, N = 1e5 + 5, M = 20;
int n, book[N], ans = 1, line[M], g[maxn], a[M][M], en, dp[M][maxn], num, lim[M];
inline void init(int x) {for (rg int i = 1; i <= 11; i++) {if (i == 1) a[i][1] = x;else a[i][1] = a[i - 1][1] * 3;if (a[i][1] > n) break;en = i, line[i] = 1, book[a[i][1]] = 1;for (rg int j = 2; j <= 18; j++) {a[i][j] = a[i][j - 1] << 1;if (a[i][j] > n) break;line[i] = j;book[a[i][j]] = 1;}lim[i] = (1 << line[i]) - 1; //第 i行的数有多少个 }
}
inline void solve(int x) {num = 0;for (rg int i = 0; i <= lim[1]; i++) {dp[1][i] = g[i];}for (rg int i = 2; i <= en; i++) {for (rg int j = 0; j <= lim[i]; j++) {if (!g[j]) continue;dp[i][j] = 0;for (rg int k = 0; k <= lim[i - 1]; k++) {if (g[k] && ((k & j) == 0)) {dp[i][j] += dp[i - 1][k];dp[i][j] %= mod;}}}}for (rg int i = 0; i <= lim[en]; i++) {num += dp[en][i];num %= mod;}
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;for (rg int i = 0; i <= maxn; i++) {g[i] = ((i << 1) & i) ? 0 : 1;}for (rg int i = 1; i <= n; i++) {if (!book[i]) {init(i);solve(i);ans = ans * num % mod;}}cout << ans << "\n";return qwq;
}
例题6:学校食堂
题目描述:
若前一道菜的对应的口味是a,这一道为b,则做这道菜所需的时间为\((a | b)-(a \& b)\),而做第一道菜是不需要计算时间的。学校食堂偶尔会不按照大家的排队顺序做菜,以缩短总的进餐时间。不过每个同学还是有一定容忍度的,队伍中的第i个同学,最多允许紧跟他身后的\(B_i\)个人先拿到饭菜。求在满足所有人的容忍度这一前提下,学校食堂做完这些菜最少需要多少时间。
解析:
设\(f[i][j][k]\)表示第1个人到第i-1个人已经打完饭,第i个人及后面7个人是否打饭的状态为j,当前最后一个打饭的人的编号为i+k(k的范围为-8到7),那么转移为:
(1)当\(j \& 1\)为真(从右往左数状态),就表示第i个人已经打完饭,i之后的7个人中,还没打完饭的人就再也不会插入到第i个人前面了。所以这时候可以转移到\(f[i + 1][j>>1][k-1]\),即\(f[i + 1][j>>1][k-1] = \min(f[i+1][j>>1][k-1], f[i][j][k])\),不需要积累时间(因为在\(j\&1\)为真的情况下,\(f[i][j][k]\)和\(f[i+1][j>>1][k-1]\)的意义是一样的)。
为什么意义是一样的呢?可以看出,最后一个打饭的人的编号为\((i+1)+(k-1)=i-k\),和\(f[i][j][k]\)表示的一样。当第i个人已经打完饭,则后面的人不能再影响到第i个人当前的状态,所以直接转移。
(2)当\(j \& 1\)为假时,是没办法转移到\(f[i+1]\)的,因为i+1之前的人还没有打完饭。但是这时候可以把i以及i之后的7个人中选出一个人打饭,也就是枚举h从0到7,\(f[i][j | (1 << h)][h] = min(f[i][j|(1 << h)][h], f[i][j][k] + time(i + k, i + h))\),其中\(time(i,j)\)表示如果上一个人编号为i,当前的人编号为j,那么编号为j的人做菜需要的时间。当然,这个转移需要考虑到忍耐度的问题。这样,在i和i之后的7个人,不是每一个还未打饭的人都可以先打的。所以用r来统计目前为止未打饭的人的忍受范围(忍受范围指能忍受在其之前打饭的最大位置)的最小值。对于任意一个人,如果\(i+h>r\),就表示他无法满足编号在他之前的所有人的忍受范围,就不需要考虑这个人。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1100, M = 256;
int c, n, t[N], b[N], f[N][M][20];
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> c;while (c--) {memset(f, 0x3f3f3f3f, sizeof(f));f[1][0][7] = 0;cin >> n;for (rg int i = 1; i <= n; i++) {cin >> t[i] >> b[i];}for (rg int i = 1; i <= n; i++) {for (rg int j = 0; j < M; j++) {for (rg int k = -8; k <= 7; k++) {if (f[i][j][k + 8] == 0x3f3f3f3f) continue;if (j & 1) f[i + 1][j >> 1][k + 8 - 1] = min(f[i + 1][j >> 1][k + 8 - 1], f[i][j][k + 8]);else {int lim = 2e9;for (rg int l = 0; l <= 7; l++) {if (!((j >> l) & 1)) { //枚举j状态里还没吃过饭的人 if (i + l > lim) break;lim = min(lim, i + l + b[i + l]); //看i+l这个人最大能忍受到后面哪个位置的人先吃 if (i + k) f[i][j | (1 << l)][l + 8] = min(f[i][j | (1 << l)][l + 8], f[i][j][k + 8] + (t[i + k] ^ t[i + l]));else f[i][j | (1 << l)][l + 8] = min(f[i][j | (1 << l)][l + 8], f[i][j][k + 8]);}}}}}}int ans = 2e9;for (rg int i = 0; i <= 8; i++) {ans = min(ans, f[n + 1][0][i]);}cout << ans << "\n";}return qwq;
}
例题7:愤怒的小鸟
题目描述:
题目入口
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = (1 << 18) + 100;
int t, n, m;
struct node { //小猪的坐标 double x, y;
} pig[20];
int st[20][20], vis[20];
int dp[N];
inline int calc(int d1, int d2) {double x1 = pig[d1].x, y1 = pig[d1].y;double x2 = pig[d2].x, y2 = pig[d2].y;if (x1 == x2) return qwq;double tx = x1 * x1 * x2 - x2 * x2 * x1, ty = y1 * x2 - y2 * x1;double a = ty / tx, b = (y1 - a * x1 * x1) / x1;if (a >= 0) return qwq; //抛物线开口应应朝下int res = 0; //记录这条抛物线能干掉的小猪 vis[d1] = vis[d2] = 1; //当前两只可以干掉for (rg int i = 1; i <= n; i++) {double x = pig[i].x, y = pig[i].y;if (fabs(a * x * x + b * x - y) < 1e-7) {res |= 1 << (i - 1);dp[1 << (i - 1)] = dp[res] = 1; //单独和顺带都是1,因为有可能所有的点都经过完了,就剩下它自己了,那也需要一条抛物线 }}return res;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> t;while (t--) {memset(dp, 0x3f, sizeof(dp));memset(vis, 0, sizeof(vis));cin >> n >> m;for (rg int i = 1; i <= n; i++) {cin >> pig[i].x >> pig[i].y;dp[1 << (i - 1)] = 1; //初始化只射一只小猪 }for (rg int i = 1; i <= n; i++) { //两只小猪一起消灭的抛物线 for (rg int j = 1; j < i; j++) {st[i][j] = calc(i, j); //st[i][j]如果同时消灭i和j两只小猪,这个抛物线会顺带着把哪些小猪消灭}}for (rg int i = 1; i <= (1 << n) - 1; i++) { //枚举每个状态 for (rg int j = 1; j <= n; j++) { //枚举下一个没被消灭的小猪if (((i >> (j - 1)) & 1) == 1) continue; //已经干掉,跳过 for (rg int k = 1; k <= j; k++) { //枚举另一个活着的小猪一起组成的抛物线 if (((1 << (k - 1)) & 1) == 1) continue;dp[i | st[j][k]] = min(dp[i | st[j][k]], dp[i] + 1); }dp[i | (1 << (j - 1))] = min(dp[i | (1 << (j - 1))], dp[i] + 1); //只能单独消灭的小猪 }}cout << dp[(1 << n) - 1] << "\n";}return qwq;
}
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
int T, n, m, line[19][19], lim, f[1 << 18], zj[1 << 18];
double x[19], y[19];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> T;for (rg int i = 0; i < (1 << 18); i++) {rg int j = 1;for (; j <= 18 && (i & (1 << (j - 1))); j++);zj[i] = j;} //预处理第一个没被打得猪,存在zj[]里,zj[i]表示i状态里第一个不为1的位置,也就是第一个没被打下来的猪的位置while (T--) {memset(f, 0x3f3f3f3f, sizeof(f));memset(line, 0, sizeof(line));cin >> n >> m;lim = (1 << n);for (rg int i = 1; i <= n; i++) cin >> x[i] >> y[i];for (rg int i = 1; i <= n; i++) {for (rg int j = i + 1; j <= n; j++) {double a = ((y[i] * x[j]) - y[j] * x[i]) * 1.0 / (x[i] * x[i] * x[j] - x[j] * x[j] * x[i]);double b = (y[i] - a * x[i] * x[i]) * 1.0 / x[i];if (a >= 0) continue;for (rg int k = 1; k <= n; k++) {if (abs(x[k] * x[k] * a + x[k] * b - y[k]) <= 1e-7) {line[i][j] |= (1 << (k - 1));}}}}f[0] = 0;for (rg int s = 0; s < lim - 1; s++) {rg int i = zj[s]; //省去一层循环for (rg int j = i + 1; j <= n; j++) {if (!((1 << (j - 1)) & s)) {if (f[s | line[i][j]] > f[s] + 1) f[s | line[i][j]] = f[s] + 1;}}if (f[s | (1 << (i - 1))] > f[s] + 1) f[s | (1 << (i - 1))] = f[s] + 1;}cout << f[lim - 1] << "\n";}return qwq;
}
例题8:寿司晚宴
题目描述:
有n-1种寿司,编号为\(1,2,3 \cdots ,n-1\),其中第i种寿司的美味度为i+1。规定一种品尝方案为不和谐的当且仅当:小G品尝的寿司中存在一种美味度为x的寿司,小W品尝的寿司中存在一种美味度为y的寿司,而x与y不互质。
现在小G和小W希望统计一共有多少种和谐的品尝方案(答案对p取模)。注意一个人可以不吃任何寿司。
解析:
首先,要让两个人选的数字全部互质,有一个显然的充要条件:甲选的数字的质因数集合和乙选的质因数集合没有交集。
当\(n \le 30\)时,可用的质数只有10个。
设\(dp[S_1][S_2]\)表示甲选择的质因数集合是\(S_1\),乙是\(S_2\)的总情况数,对于每个\(2\sim n\)分解质因数,把每个质因数是否出现状压起来存下来,dp的时候从前往后扫,那么可以刷表法做一波\(dp[i][S_1 | k][S_2] += dp[i-1][S_1][S_2](k \&S_2 = 0)\),或者\(dp[i][S_1][S_2 | k] += dp[i - 1][S_1][S_2](k \& S_1 = 0)\),其中k是当前数的质因数集合。
滚动数组优化一下,把第一维去掉,总效率是\(O(2^{20}n)\)。
而当n到了500以后可用的质因数变多,我们无法把它们全部压进一个数里面了。
注意到,一个小于500的数,最多只可能有1个比22大的质因子,所以我们可以把这个质因子单独拿出来记录一下(没有就记为0),然后我们把\(2 \sim n\)这些数按照大质因子大小排序,这样令大质因子相同的数排在一起(也就是不能甲乙同时选的)。
我们记录三个相同数组:\(dp[S_1][S_2], f1[][], f2[][]\)。其中f1表示这个大质因子让第一个人选,f2表示这个大质因子让第二个人选。因为小质因数只有8个,所以\(0 \le S_1,S_2 \le 255\)。对于每一段大质因子相同的数,我们在这一段开始的时候把dp的值赋给f1和f2,然后在这一段内部用刷表法推f1和f2。
具体地讲,\(f1[i][S_1|k][S_2] += f1[i-1][S_1][S_2](k \& S_2 = 0)\)或者\(f2[i][S_1][S_2|k] += f2[i-1][S_1][S_2](k \& S_1 = 0)\)。其中k是当前数的最小质因数集合。
这一段数推完以后,再把\(f1, f2\)合并到dp里面,\(dp[S_1][S_2] = f1[S_1][S_2] + f2[S_1][S_2] - dp[S_1][S_2]\)。这里减掉一个dp是因为两种情况会重复统计两个人都不选的情况(也就是原来的\(dp[S_1][S_2]\)的值)。
最后答案就是\(dp[0][0] \sim dp[255][255]\)的和。总时间复杂度为\(O(2^{16}n)\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
struct node {int v, big, S;
} num[510];
ll dp[260][260], f1[260][260], f2[260][260];
int p[10] = {0, 2, 3, 5, 7, 11, 13, 17, 19};
int n, mod;
bool cmp(node x, node y) {return x.big < y.big;
}
void resolve(int x) { //求大质因子rg int tmp = num[x].v;num[x].big = -1;for (rg int i = 1; i <= 8; i++) {if (tmp % p[i] != 0) continue;num[x].S |= (1 << (i - 1));while (tmp % p[i] == 0) tmp /= p[i];}if (tmp != 1) num[x].big = tmp;
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> mod;for (rg int i = 1; i < n; i++) {num[i].v = i + 1;resolve(i);}sort(num + 1, num + n, cmp); //按照大质因子排序,相同的大质因子就连在一起了,我们只需关心小质因子的分配情况即可 dp[0][0] = 1;for (rg int i = 1; i < n; i++) {if (i == 1 || num[i - 1].big != num[i].big || num[i].big == -1) { //此时的i属于下一个大质数块的开头,首先需要把dp的值赋值给f1,f2memcpy(f1, dp, sizeof(dp));memcpy(f2, dp, sizeof(f2));}for (rg int j = 255; j >= 0; j--) { //滚动数组优化,需要倒序枚举,如果是同一个大质因子,那只关心小质因子的选择情况 for (rg int k = 255; k >= 0; k--) {if (j & k) continue;if ((num[i].S & k) == 0) f1[j | num[i].S][k] += f1[j][k];if ((num[i].S & j) == 0) f2[j][k | num[i].S] += f2[j][k];f1[j][k] %= mod;f2[j][k] %= mod;}}if (i == n - 1 || num[i].big != num[i + 1].big || num[i].big == -1) { //同一个大质因子块中要合并,因为大质因子放谁都有可能,所以合并是相加for (rg int j = 255; j >= 0; j--) {for (rg int k = 255; k >= 0; k--) {if (j & k) continue;dp[j][k] = ((f1[j][k] + f2[j][k]) % mod + mod - dp[j][k]) % mod;}} }}ll ans = 0;for (rg int i = 0; i <= 255; i++) {for (rg int j = 0; j <= 255; j++) {if ((j & i) == 0 && dp[i][j]) ans = (ans + dp[i][j]) % mod;}}cout << ans << "\n";return qwq;
}
例题9:Tourist Attractions
题目描述:
题目入口
解析:
令\(f[s][i]\)表示现在已经在s集合中的城市停留并且现在在第i个城市的最短路径长度。令\(u_i\)表示第i个城市的前置集合。
那么\(f[s][i]\)成立的条件是\(u_i \subset s\),有转移方程:
\(f[s][i] = min_{j \in s-i}\{f[s -i][j] + dis[j][i]\}\)
边界条件为\(f[i][i] = dis[1][i]\),\(u_i = \varnothing\)。
容易想到先用\(dijkstra\)跑k个点的最短路,算出两两之间的dis,然后转移。
但这样会\(MLE\),使用滚动数组。观察转移方程,发现转移集合s需要用到的集合大小只比s小1,那么可以先处理每个集合的元素个数,把集合大小作为拓扑序,就可以使用滚动数组了。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e4 + 5, M = 2e5 + 5;
struct node {int v, w;bool operator < (const node &b) const {return w > b.w;}
};
int n, m, k, Q, uset[21];
int tl[21][21], mapp[21], kdis[21][2], sum[(1 << 20) + 1];
int f[2][184757][21], cur, pmap[(1 << 20) + 1];
vector<int> p[21];
vector<node> s[N];
priority_queue<node> q;
int dis[N];
bool vis[N];
inline void dijkstra(int u) {memset(dis, 0x3f, sizeof(dis));dis[mapp[u]] = 0;memset(vis, 0, sizeof(vis));q.push({mapp[u], 0});while (!q.empty()) {node x = q.top();q.pop();if (vis[x.v]) continue;vis[x.v] = 1;for (rg int i = 0; i < s[x.v].size(); i++) {node t = s[x.v][i];if (!vis[t.v] && dis[t.v] > dis[x.v] + t.w) {dis[t.v] = dis[x.v] + t.w;q.push({t.v, dis[t.v]});}}}kdis[u][0] = dis[1];kdis[u][1] = dis[n];for (rg int i = 0; i < k; i++) {tl[u][i] = dis[mapp[i]];}
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m >> k;for (rg int i = 1; i <= m; i++) {rg int u, v, w;cin >> u >> v >> w;s[u].push_back({v, w});s[v].push_back({u, w});}if (k == 0) {mapp[1] = 1;dijkstra(1);cout << dis[n] << "\n";return qwq;}for (rg int i = 0; i < k; i++) {mapp[i] = i + 2;}for (rg int s = 1; s < (1 << k); s++) {sum[s] = sum[s & (~(s & -s))] + 1;p[sum[s]].push_back(s);pmap[s] = p[sum[s]].size() - 1;}cin >> Q;while (Q--) {rg int u, v;cin >> u >> v;uset[v - 2] |= (1 << (u - 2));}memset(f, 0x3f, sizeof(f));for (rg int i = 0; i < k; i++) {dijkstra(i);if (!uset[i]) f[0][pmap[1 << i]][i] = kdis[i][0];}for (rg int w = 2; w <= k; w++) {cur ^= 1;memset(f[cur], 0x3f, sizeof(f[cur]));for (rg int e = 0; e < p[w].size(); e++) {rg int s = p[w][e];for (rg int i = 0; i < k; i++) {if ((s & (1 << i)) && ((uset[i] & (s & (~(1 << i)))) == uset[i])) {for (rg int j = 0; j < k; j++) {if (i != j && (s & (1 << j))) {f[cur][e][i] = min(f[cur][e][i], f[cur ^ 1][pmap[s & (~(1 << i))]][j] + tl[j][i]);}} }}}}int ans = 0x3f3f3f3f;for (rg int i = 0; i < k; i++) {ans = min(ans, f[cur][0][i] + kdis[i][1]);}cout << ans << "\n";return qwq;
}
例题10:排列
题目描述:
题目入口
解析:
设\(dp[S][k]\)表示现在所选的状态集合为S,当前所选的数组成的数字对d取余后的值为k。
转移时首先枚举所有的状态S,然后再枚举所有没有被选的数j,再枚举余数k即可转移。
转移方程为:
\(dp[S|(1 << (j-1))][(k \times 10 + a[j]) \% d] += dp[S][k]\)
但这样是错误的,因为没有考虑重复的排列,比如S为"001",结果发现"010"这个状态会被算两次,因此需要去重。
法一:
如果某个数字i在排列中出现了\(cnt[i]\)次,那么最后的答案\(\texttt{ans}\)是\(ans /= (cnt[i])!\)
法二:
用数组标记i有没有被填过。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 12;
int T, d, a[N], cnt, dp[1 << N][1002];
bool vis[N];
char s[N];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> T;int len;while (T--) {memset(dp, 0, sizeof(dp));cin >> s + 1 >> d;len = strlen(s + 1);cnt = 0;for (rg int i = 1; i <= len; i++) {a[i] = s[i] - '0';}dp[0][0] = 1;for (rg int s = 0; s < (1 << len); s++) {memset(vis, 0, sizeof(vis));for (rg int j = 1; j <= len; j++) {if (!(s & (1 << (j - 1))) && !vis[a[j]]) { //如果a[j]已经转移过就不能继续转移了,j表示遍历s中的各位数字 vis[a[j]] = 1;for (rg int k = 0; k < d; k++) { //k表示对d取余后的数 dp[s | (1 << (j - 1))][(k * 10 + a[j]) % d] += dp[s][k]; //s|(1<<(j-1))表示把右数第k位变为1}}}}cout << dp[(1 << len) - 1][0] << "\n"; }return qwq;
}
例题11:Bill的挑战
题目描述:
题目入口
解析:
枚举位数,维护数组\(g[i][j]\)表示第i位数下放j的情况下该列的匹配情况。
定义\(f[i][j]\)表示T串已经匹配了i位,且与n个字符串是否匹配的集合为j,状态边界为lim,\(f[0][lim - 1] = 1\),首先枚举位数,然后枚举状态,如果\(f[i][j] = 0\)则不需要进行操作,然后枚举字符,在下一状态下添加字符的种类数为本状态加上下一状态的原种类数。
最后枚举不同状态,记录该状态与原数组的匹配情况,判断该状态是否包括某一行的位数(即该行匹配),如果是则\(tot++\),如果\(tot = m\),累加ans。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 100005, mod = 1e6 + 3;
int f[55][1 << 15], g[55][30];
char s[16][55];
int T, n, m;
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> T;while (T--) {memset(f, 0, sizeof(f));memset(g, 0, sizeof(g));cin >> n >> m;for (rg int i = 0; i < n; i++) {cin >> s[i];}int len = strlen(s[0]);for (rg int i = 0; i < len; i++) { //枚举位数 for (rg int j = 0; j < 26; j++) { //枚举字符 for (rg int k = 0; k < n; k++) { //枚举行数 if (s[k][i] == '?' || s[k][i] == j + 'a') {g[i][j] |= (1 << k); //位数为i时j字符的匹配情况,右数第k位变为1 }}}}int lim = (1 << n);f[0][lim - 1] = 1;for (rg int i = 0; i < len; i++) { //枚举位数 for (rg int j = 0; j < lim; j++) { //枚举状态 if (f[i][j]) {for (rg int k = 0; k < 26; k++) { //枚举字符 f[i + 1][j & g[i][k]] = (f[i + 1][j & g[i][k]] + f[i][j]) % mod;}}}}int ans = 0;for (rg int i = 0; i < lim; i++) { //枚举状态 int tot = 0;for (rg int j = 0; j < n; j++) {if (i & (1 << j)) tot++;}if (tot == m) ans = (ans + f[len][i]) % mod;}cout << ans << "\n";}return qwq;
}
例题12:Disease Manangement
题目描述:
有N头牛,他们可能患有D种病,现在从这些牛中选出若干头且选出来的牛所患的病不超过K种。输出方案数。
解析:
令\(f[i]\)表示选出的疾病状态为i的最多牛数,\(t[i]\)表示i这头牛的疾病状态。
状态转移方程:\(f[j | t[i]] = max(f[j | t[i]], f[j] + 1)\)
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
int N, K, D, tot, num, ans;
int t[1005], f[1 << 15];
inline bool check(int x) { //统计x中1的数量,即患病总数是否小于K种 rg int cnt = 0;for (rg int i = 0; i < D; i++) {if ((x >> i) & 1) cnt++;}return (cnt <= K);
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> N >> D >> K;tot = (1 << D) - 1;for (rg int i = 1; i <= N; i++) {cin >> num;for (rg int j = 1; j <= num; j++) {rg int x;cin >> x;t[i] |= (1 << (x - 1)); //第x位变为1 }}for (rg int i = 1; i <= N; i++) {for (rg int j = tot; j >= 0; j--) {f[j | t[i]] = max(f[j | t[i]], f[j] + 1);}}for (rg int i = 0; i <= tot; i++) {if (check(i)) ans = max(ans, f[i]);}cout << ans << "\n";return qwq;
}
例题13:动物园
题目描述:
题目入口
解析:
首先,因为每个小朋友只能看见5个围栏,数据范围很小,其次小朋友是否满意只与这五个围栏有关,那么考虑壮压dp。
考虑到可能小朋友看见的围栏范围可能相同,那么我们可以预处理\(num[pos][s]\),表示从第pos个围栏开始的五个围栏状态为s时会有多少个小朋友满意。定义状态\(f[i][s]\)表示枚举到第i个围栏且\([i,i+4]\)的围栏移走状为s时的最多满意人数。则\(f[i][s]\)可以由第i-1个围栏移走和不移走两种状态转移得来:
\(f[i][s] = max(f[i - 1][(s \& 15) << 1], f[i - 1][(s \& 15) << 1 | 1]) + num[i][s]\)(15转成二进制是1111)
其次要注意的是在dp之前先枚举前5个的状态state,因为围栏是一个环,最后枚举第n+1个围栏时,其实就相当于又回到了第一个围栏,那么此时必须满足\(s = state\)才是有效状态,更新答案。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 50010;
int n, m, ans, f[N][40], num[N][40];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int a, b, c, l, d, t;cin >> n >> m;for (rg int i = 1; i <= m; i++) {cin >> a >> b >> c;l = d = 0;for (rg int j = 1; j <= b; j++) {cin >> t;t = (t - a + n) % n;l |= 1 << t;}for (rg int j = 1; j <= c; j++) {cin >> t;t = (t - a + n) % n;d |= 1 << t;}for (rg int j = 0; j < 32; j++) {if ((j & l) || (~j & d)) num[a][j]++;}}for (rg int i = 0; i < 32; i++) {memset(f[0], 128, sizeof(f[0]));f[0][i] = 0;for (rg int j = 1; j <= n; j++) {for (rg int s = 0; s < 32; s++) {f[j][s] = max(f[j - 1][(s & 15) << 1], f[j - 1][(s & 15) << 1 | 1]) + num[j][s];}}if (ans < f[n][i]) ans = f[n][i];}cout << ans << "\n";return qwq;
}
例题14:卡农
题目描述:
题目入口
\(\texttt{to be continued} \cdots\)
例题15:字符合并
题目描述:
题目入口
分析:
思路为区间dp+状压dp。
为了得到最大的分数我们应该尽量合并到数字不能合并为止,于是最终得到的01串中的每一个数字还原后是一系列不相交的区间,我们考虑用区间dp的思想来转移状态。
令\(f[i][j][t]\)表示原串中第i到第j个数字最终合并成t的状态的最大分数。
我们枚举中间的断点mid,上文已证区间不相交,于是不妨使mid右边的子串合并成t的最后一位数字,mid左边的合并成其他位的数字。因为能合并成1为数字的原串长度可以为\(1,k,2k-1,\cdots\),所以我们每次将mid的值改变k-1即可。并且进一步可以得到,当串的长度为\(t(k-1)+1\)时,该串的长度为\((len-1)\bmod(k-1)+1\)。
另有一种特殊情况,即i到j恰好有k位数字,我们直接把它合并一次。用一个辅助数组存储最大值(直接修改f数组可能会导致修改后的数能够再修改成其他数组元素)。
最后的答案就是\(\max\{f[1][n][所有状态]\}\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 303;
const ll inf = 2305843009213693951;
int n, k;
ll a[N], c[N], f[N][N][1 << 8], g[2], w[1 << 8];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> k;for (rg int i = 1; i <= n; i++) cin >> a[i];for (rg int i = 0; i < (1 << k); i++) cin >> c[i] >> w[i];for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {for (rg int s = 0; s < (1 << k); s++) {f[i][j][s] = -inf;}}}for (rg int i = 1; i <= n; i++) f[i][i][a[i]] = 0;for (rg int len = 2; len <= n; len++) {for (rg int l = 1; l + len - 1 <= n; l++) {rg int r = l + len - 1, x = (len - 1) % (k - 1);if (x == 0) x = k - 1;for (rg int mid = r - 1; mid >= l; mid -= k - 1) {for (rg int s = 0; s < (1 << x); s++) {f[l][r][s << 1] = max(f[l][r][s << 1], f[l][mid][s] + f[mid + 1][r][0]);f[l][r][s << 1 | 1] = max(f[l][r][s << 1 | 1], f[l][mid][s] + f[mid + 1][r][1]);}}if (x == k - 1) {g[0] = g[1] = -inf;for (rg int s = 0; s < (1 << k); s++) {g[c[s]] = max(g[c[s]], f[l][r][s] + w[s]);}f[l][r][0] = g[0];f[l][r][1] = g[1];}}}rg ll ans = -inf;for (rg int i = 0; i < (1 << k); i++) {ans = max(ans, f[1][n][i]);}cout << ans << "\n";return qwq;
}
例题16:[yLOI2020] 凉凉
首先需要预处理:
- 1.在一个深度建立一个铁路线i花费的价格\(cost_{i,j}\)。
- 2.处理出铁路线i和铁路线j能否在同一个深度建立线路\(vis_{i,j}\)。
- 3.处理出在深度为i,这一层深度修建的铁路线的状态为\(S\)的价钱\(g_{i,S}\)。
令\(f_{i,S}\)为已经弄完了前i深度的铁路线,现在建立完的铁路线编号的状态为\(S\)的最小价格。
\(f_{i,S}= \displaystyle min_{s\in S}\{f_{i-1,S or s}+g_{i,s}\}\)
我们可以用枚举子集的方法避免暴力枚举状态判断。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 15, M = 1e5 + 3, K = 1 << 15, inf = 2e18;
int n, m;
int dep[N][M]; //深度为i的地铁经过地铁站j的花费
int cnt[N]; //第i条地铁经过的站点个数
int sub[N][M]; //第i条地铁经过的站点编号
int f[N][K]; //前i深度,修建的铁路状态为j的最小花费
int g[N][K]; //在深度为i时,该层修建状态为j的花费
int cost[N][N]; //第i条铁路在深度为j时的花费
bool vis[N][N]; //询问第i条铁路和第j条铁路能否修建在同一深度
int stk[N], top;
inline void init() {for (rg int i = 1; i <= n; i++) {sort(sub[i] + 1, sub[i] + 1 + cnt[i]);}for (rg int i = 1; i <= n; i++) { //预处理vis[][] for (rg int j = i + 1; j <= n; j++) {vis[i][j] = vis[j][i] = true;rg int x = 1, y = 1;while (x <= cnt[i] && y <= cnt[j]) {if (sub[i][x] == sub[j][y]) {vis[i][j] = vis[j][i] = false;break;}if (sub[i][x] < sub[j][y]) x++;else y++;}}}for (rg int s = 1; s < (1 << n); s++) { //预处理g[][] top = 0;for (rg int i = 1; i <= n; i++) {if (s & (1 << (i - 1))) { //找到s状态的第i条铁路线stk[++top] = i;for (rg int j = 1; j < top; j++) { //枚举s状态的其他铁路线 if (!vis[i][stk[j]]) { //两线路不能在同一深度 for (rg int k = 1; k <= n; k++) {g[k][s] = inf; //不能选,设为极大值 }}}if (g[1][s] == inf) break;for (rg int j = 1; j <= n; j++) {g[j][s] += cost[i][j]; //深度为j时修建状态为s的铁路,加上第i条铁路线在j深度时的总价钱}}}}for (rg int s = 1; s < (1 << n); s++) {f[1][s] = g[1][s]; //初始化第一行 }
}
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= m; j++) {cin >> dep[i][j];}}for (rg int i = 1; i <= n; i++) {cin >> cnt[i];for (rg int j = 1; j <= cnt[i]; j++) {cin >> sub[i][j];}for (rg int j = 1; j <= n; j++) {for (rg int k = 1; k <= cnt[i]; k++) {cost[i][j] += dep[j][sub[i][k]]; //预处理cost[][]}}}init();for (rg int i = 2; i <= n; i++) {for (rg int S = 0; S < (1 << n); S++) {f[i][S] = f[i - 1][S];for (rg int s = S; s; s = (s - 1) & S) { //枚举子集f[i][S] = min(f[i][S], f[i - 1][S ^ s] + g[i][s]);}}}cout << f[n][(1 << n) - 1] << "\n";return qwq;
}





![[DP] [倍增优化] Luogu P1081 [NOIP2012 提高组] 开车旅行](https://cdn.luogu.com.cn/upload/image_hosting/zgms0k7y.png)