昨天端午gap了一天,今天继续。
之前都是零散地做题,感觉缺乏体系,今天开始就着labuladong的算法小抄来做题,顺便记下自己的阅读笔记。
核心套路篇1
首先是第一章,核心套路篇,这一章主要介绍算法解题的通用思路。
数据结构的核心是数组和链表,其它都是基于此二者的变体。
数据结构操作就是增删改查四种,操作对象具体分为数组、链表以及二叉树三种框架。实际上,二叉树的遍历就是链表遍历的拓展。
作者说,刷题先刷二叉树,因为二叉树最能培养框架思维,实现一通百通。
二叉树中的最大路径和
题目描述:路径和是路径中各节点值的总和。给你一个二叉树的根节点 root ,返回其最大路径和。
示例:
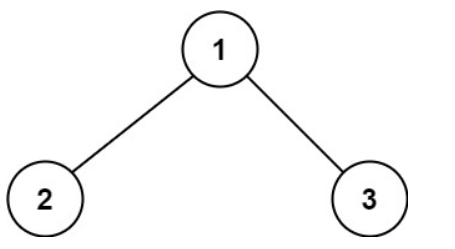
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
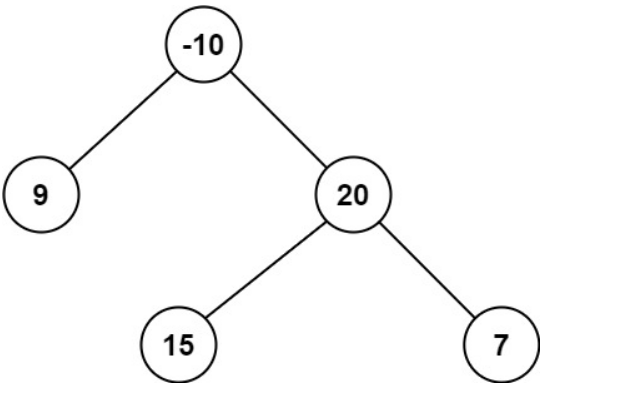
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
问题
- 这里只给出了树的序列化数组,是不是还要先还原成二叉树呢?
不,实际上代码中已经给出了树的根节点 - 要求出最大路径,是不是要用动态规划或者回溯呢?
不,只需要每一步进行贪心求解。
思路核心 - 递归
- 自己加左右子树的路径就是一条路径/自己作为路径的一部分时就只能选择左右子树的其中一个
- 怎么样能比较左右子树的最大值呢,那当然是先遍历它们,再进行比较,这就是后序遍历
- 用一个变量记录下全局的最大值即可
注意 - 这里的最大路径变量需要是全局变量
- 获得左右子树路径和时,需要与0做个max,因为只有大于0的路径才对总和有意义
- 每次计算经过自己的左右子节点(若小于0则不经过)以及自己时的路径
- 返回时只能选择一边加自己返回
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 以上给出了树的定义
class Solution:def __init__(self):# 初始化为最小值,用于记录最大路径和self.max_sum = -infdef maxPathSum(self, root: Optional[TreeNode]) -> int:# 获得root节点对应树的最大路径和self.getMaxPathSum(root)return self.max_sum# 定义递归函数def getMaxPathSum(self, root):# 处理边界条件if root==None:return 0left = max(0, self.getMaxPathSum(root.left))right = max(0, self.getMaxPathSum(root.right))self.max_sum = max(self.max_sum,root.val+left+right)return max(left,right) + root.val

![[Paper Reading] Tesla AI Day for FSD Beta](https://img2024.cnblogs.com/blog/1067530/202406/1067530-20240611210527658-1559677080.png)