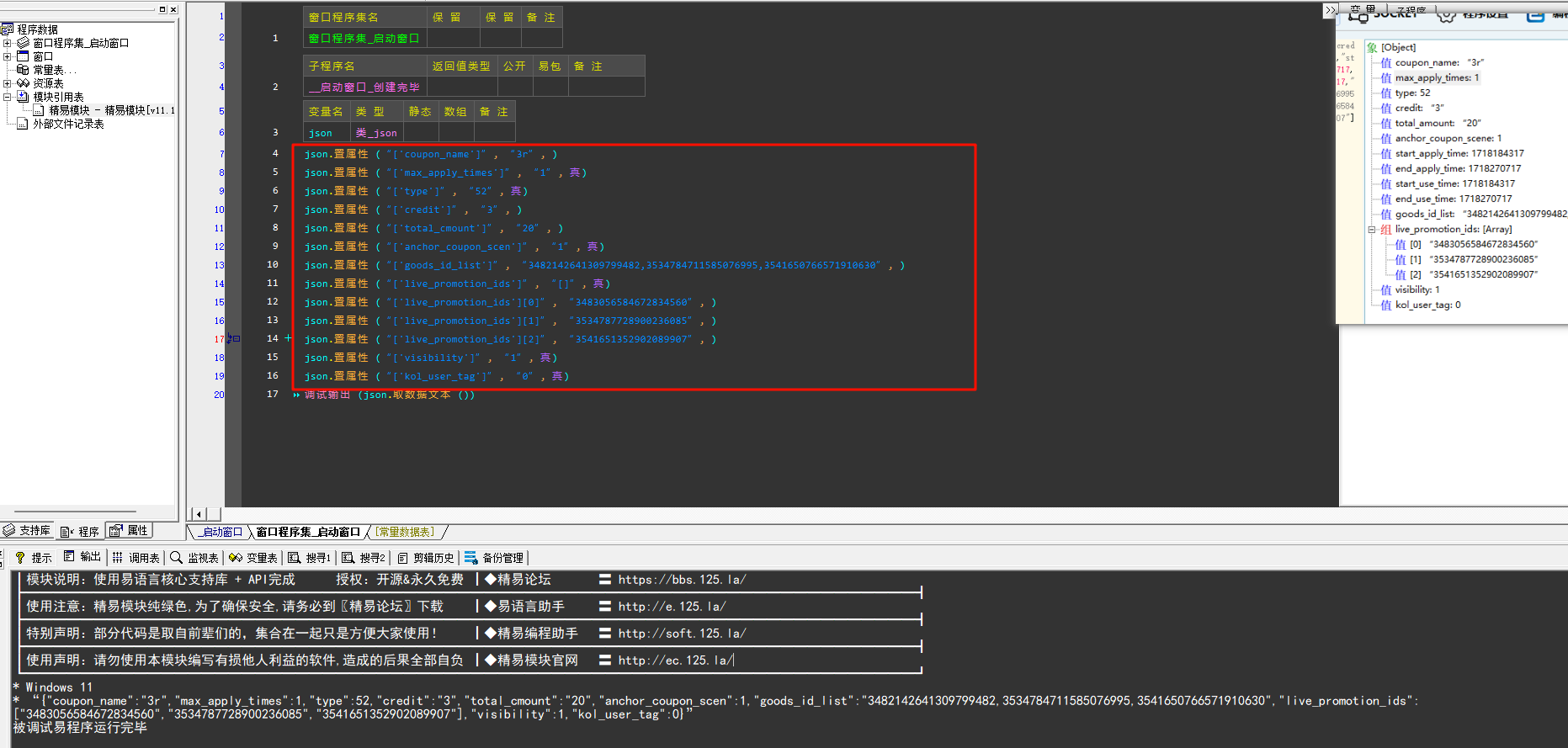
相机与变换
一、内参与外参概念
在计算机视觉中,特别是在相机标定和立体视觉领域,内参(intrinsic parameters)和外参(extrinsic parameters)是非常重要的概念。它们与相机的几何属性和姿态有关。
- 内参(Intrinsic Parameters): 内参是描述相机内部属性的参数,包括焦距、主点(光学中心)坐标、畸变系数等。内参通常在相机标定时确定,因为它们通常对于特定相机型号是固定的,不随时间变化。一旦相机内参被确定,它们在相机的使用过程中通常是保持不变的。
- 外参(Extrinsic Parameters): 外参是描述相机在世界坐标系中的位置和姿态的参数,通常包括旋转矩阵和平移向量。外参在不同的相机位置或拍摄时刻可能会发生变化。例如,在立体视觉中,如果有两个相机,那么它们的相对位置和方向会在每次移动相机时发生变化,从而导致外参的变化。
如果相机不发生位置和方向的变化,比如相机固定在一个固定位置,那么外参在很长一段时间内可能保持不变。然而,如果相机的位置或方向发生变化,例如移动相机或更改拍摄角度,外参会随之变化。
二、四个坐标系
四个坐标系的意义,世界坐标系(参考坐标系)、摄像机坐标系 、图像物理坐标系和像素坐标系。
- 世界坐标系就是物体在真实世界中的坐标,比如黑白棋盘格的世界坐标系原点定在第一个棋盘格的顶点,Xw,Yw,Zw互相垂直,Zw方向就是垂直于棋盘格面板的方向。可见世界坐标系是随着物体的大小和位置变化的,单位是长度单位。只要棋盘格的大小决定了,无论板子怎么动,棋盘格角点坐标一般就不再变动(因为是相对于世界坐标系原点的位置不变),且认为是Zw=0。
- 相机坐标系以光心为相机坐标系的原点,以平行于图像的x和y方向为Xc轴和Yc轴,Zc轴和光轴平行,Xc,Yc,Zc互相垂直,单位是长度单位。
- 图像物理坐标系以主光轴和图像平面交点为坐标原点,x和y方向如图所示,单位是长度单位。
- 图像像素坐标系以图像的顶点为坐标原点,u和v方向平行于x和y方向,单位是以像素计。
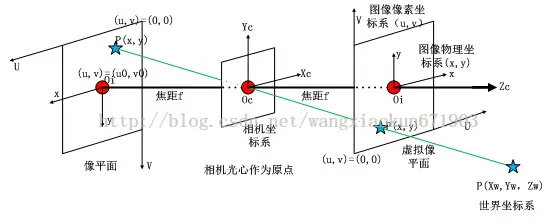
图片借用link
相机成像过程涉及到四个坐标系的变换,变换关系如下:
(U,V,W)是世界坐标系,经过刚体变换(如:旋转、平移)后变为了相机坐标系,再次经过透视投影转变为了图像坐标系,最后经仿射变换转换为了像素坐标系(u,v)。转换关系如下(Z是尺度因子):
三、相机内参
然后就来到了图中的虚线部分,考虑相机坐标下的\(P(x_c,y_c,z_c)\),焦距为\(f_c\),由相似三角形可以得到:
写成矩阵形式为:
最后得到了投影平面上图像的坐标,但要注意,我们此时仍然在物理坐标系下。即如果现在这些字母都有个单位的话,那么它们应该是米或毫米。距离我们熟悉的图片还有一步:从图像坐标系变换至像素坐标系。为了实现这一点,我们进行了水平和竖直方向的伸缩变换以及平移变换,将坐标系的原点从光心转移到(通常时候)图像的左上角:
这里\(u_0\)一般近似为\(W/2\),\(v_0\)一般近似为\(H/2\)。所以整个的这个变换过程可以整理成:
其中,\(f_x=\frac f{\mathrm{d}x},f_y=\frac f{\mathrm{d}y}\)。表示将物理坐标上的焦距映射进像素尺寸\((dx,dy)\)中的缩放,然而其实大多数情况下其实都有\(dx=dy\),即像素是一个正方形。得到的第一个矩阵简记为\(K\),也叫相机内参。获取相机内参和外参的方法即相机标定。
四、相机外参
首先,体素所在的( 整个场)有一个默认坐标系,称为世界坐标系\(O-x_{w}y_{w}z_{w}\)。不同的相机可能会从不同的角度进行拍摄。即不同的\(\phi,\theta,\) 以及此时小孔位置的三维坐标。即我们可以通过绕\(z_{w}\)轴和绕\(x_{z}\)轴旋转坐标系、然后再对坐标系进行平移,来将世界坐标系上的一个点转移到相机坐标系下的表示。假设此时相机的位置是\((x,y,z)\),那么可以先绕\(x_{w}\)轴旋转\(\phi\),再绕\(z_{w}\)轴旋转\(\theta\):
同时,平移向量可以表示为\(T=[x,y,z]\),那么我们可以通过齐次坐标构造一个位姿矩阵C:
矩阵C又叫相机外参。这样就能通过左乘将世界坐标转换成相机坐标(w2c):