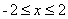ABC355E Guess the Sum
题目大意
给定一个长度为 \(2^n\) 的序列 \((A_0,A_1,\dots,A_{2^n-1})\),每次可以询问一个长度为 \(2^i\) 的区间 \([l,r]\),满足 \(l\) 是 \(2^i\) 的倍数,标准输入会返回 \([l,r]\) 的区间和 \(\bmod 10\) 的结果,要求以最少的次数计算出给定区间 \([L,R]\) 的区间和。
Solve
令 \(sum\) 为原序列的前缀和数组,询问区间 \([l,r]\) 的区间和相当于询问 \(sum_r-sum_{l-1}\)。
考虑在前缀和上建图,如果可以询问区间 \([l,r]\),那么就在 \(l-1\) 和 \(r\) 间连一条无向边。建边后从 \(L-1\) 跑单源最短路即可,可以用 BFS 跑,因为边权都是 \(1\)。
至于输出询问,我们可以对于每个点 \(i\),用 \(fa_i\) 记录它是从哪个点转移过来的,最后从 \(R\) 跑一遍 DFS 即可。
注意,原序列的下标从 \(0\) 开始,所以访问 \(sum_{0-1}\) 时会出问题,应将原序列下标整体加一。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{short f=1;int x=0;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();return x*f;
}
int n,a,b,ans,res,fa[1<<19];
vector<int>e[1<<19];
bool vis[1<<19];
void bfs()
{queue<int>q;q.push(a);vis[a]=1;while(!q.empty()){int u=q.front();q.pop();for(auto i:e[u])if(!vis[i]){fa[i]=u;vis[i]=1;if(i==-~b) return;q.push(i);}}
}
void dfs(int u)
{int len=log2(abs(fa[u]-u));if(fa[u]>u)//若转移点在当前点右侧,说明是走回头路,应减去这一段区间和。printf("? %lld %lld\n",len,u/(1<<len)),fflush(stdout)/*清空缓冲区*/,ans-=(res=read());else//否则应加上区间和printf("? %lld %lld\n",len,(fa[u])/(1<<len)),fflush(stdout),ans+=(res=read());if(res==-1) exit(0);//依题意,若询问不合法或询问次数多于最小次数标准输出会返回-1,此时退出。if(fa[u]!=a) dfs(fa[u]);//若是从起点a-1转移过来,则说明已询问完,此时不再继续询问。
}
signed main()
{n=read();a=read();b=read();for(int len=(1<<n);len;len>>=1)for(int i=1;i+len-1<=(1<<n);i=-~i)if((i-1)%len==0)//建图e[i-1].push_back(i+len-1),e[i+len-1].push_back(i-1);bfs();dfs(-~b);printf("! %lld",(ans%100+100)%100);fflush(stdout);return 0;
}
 前缀和上建图,有点典,但赛时没想出来
前缀和上建图,有点典,但赛时没想出来