本篇文章源自我在 2021 年暑假自学大气物理相关知识时手写的笔记,现转化为电子版本以作存档。相较于手写笔记,电子版的部分内容有补充和修改。笔记内容大部分为公式的推导过程。
- 7.1 大气湿度的概念
- 7.2 水汽压
- 7.2.1 水汽压
- 7.2.2 饱和水汽压
- 7.2.3 饱和差
- 7.3 混合比与比湿
- 7.3.1 水汽混合比
- 7.3.2 比湿
- 7.4 相对湿度与绝对湿度
- 7.4.1 相对湿度
- 7.4.2 绝对湿度
- 7.5 露点变化和抬升凝结高度
- 7.5.1 露点温度
- 7.5.2 抬升凝结高度(LCL)
- 7.6 两个例子理解湿度参数
- 7.6.1 往封闭空间加入水汽的例子
- 7.6.2 将封闭空间降温的例子
7.1 大气湿度的概念
表示大气中水汽量多少的物理量称大气湿度。大气湿度状况与云、雾、降水等关系密切。下面来介绍几个表示大气湿度的物理量。
7.2 水汽压
7.2.1 水汽压
大气压力是大气中各种气体压力的总和。水汽和其它气体一样,也有压力。大气中的水汽所产生的那部分压力称水汽压(用 \(e\) 表示)。它的单位和气压一样,也用 hPa 表示。假设湿空气中水汽的摩尔分数为:
其中,\(n_w\) 和 \(n_d\) 分别为水汽和干空气的摩尔数,则水汽的分压强为:
7.2.2 饱和水汽压
在温度一定情况下,单位体积空气中的水汽量有一定限度,如果水汽含量达到此限度,空气就呈饱和状态,这时的空气称饱和空气。饱和空气的水汽压称饱和水汽压(用 \(E\) 表示),也叫最大水汽压,因为超过这个限度,水汽就要开始凝结。实验和理论都可证明,饱和水汽压随温度的升高而增大。在不同的温度条件下,饱和水汽压的数值是不同的。饱和水汽压随温度的变化率由克拉珀龙-克劳修斯方程决定,即:
式中,\(e_s\) 是纯水平液面的饱和水汽压,\(R_w\) 是水汽的比气体常数,\(L_w\) 是相变潜热。
7.2.3 饱和差
在一定温度下,饱和水汽压与实际空气中水汽压之差称饱和差(用 \(d\) 表示),即:
饱和差表示实际空气距离饱和的程度。在研究水面蒸发时常用到饱和差,它能反映水分子的蒸发能力。
7.3 混合比与比湿
7.3.1 水汽混合比
一团湿空气中,水汽质量(或密度)与干空气质量(或密度)的比值称水汽混合比(用 \(r\) 表示),其单位为 g/kg,定义式如下:
其中,\(m_w\) 为湿空气中水汽的质量,\(m_d\) 为湿空气中干空气的质量;\(\rho_w\) 为湿空气的水汽分密度,\(\rho_d\) 为湿空气的干空气分密度。由于水汽和干空气均遵从理想气体状态方程,所以有:
其中,\(p\) 表示湿空气的总压强,\(e\) 表示其中水汽部分的压强(即水汽压),\(p-e\) 是干空气的压强。干空气的气体常数为 \(R_d\) 水汽的气体常数为 \(R_w\)。在地球大气可观测的温度范围内,\(p >> e\),所以有:
因此,在给定的温度条件下,混合比与总压强成反比。
对于饱和的湿空气,水汽质量与干空气质量的比值称饱和水汽混合比(又称饱和混合比),用 \(r_s\) 表示。比如,25℃ 下的饱和混合比为 20g/kg,说明每千克饱和空气中含有 20g 水汽。
7.3.2 比湿
在一团湿空气中,水汽的质量与该团空气总质量(水汽质量加上干空气质量)的比值,称比湿(用 \(q\) 表示),其单位为 g/g,即表示每一克湿空气中含有多少克的水汽(也有用每千克质量湿空气中所含水汽质量的克数表示,即g/kg)。定义式如下:
其中,\(m_w\) 为该团湿空气中水汽的质量,\(m_d\) 为该团湿空气中干空气的质量。通常大气中的混合比与比湿都小于 0.04,因此可以简单认为 \(q \approx r\)。
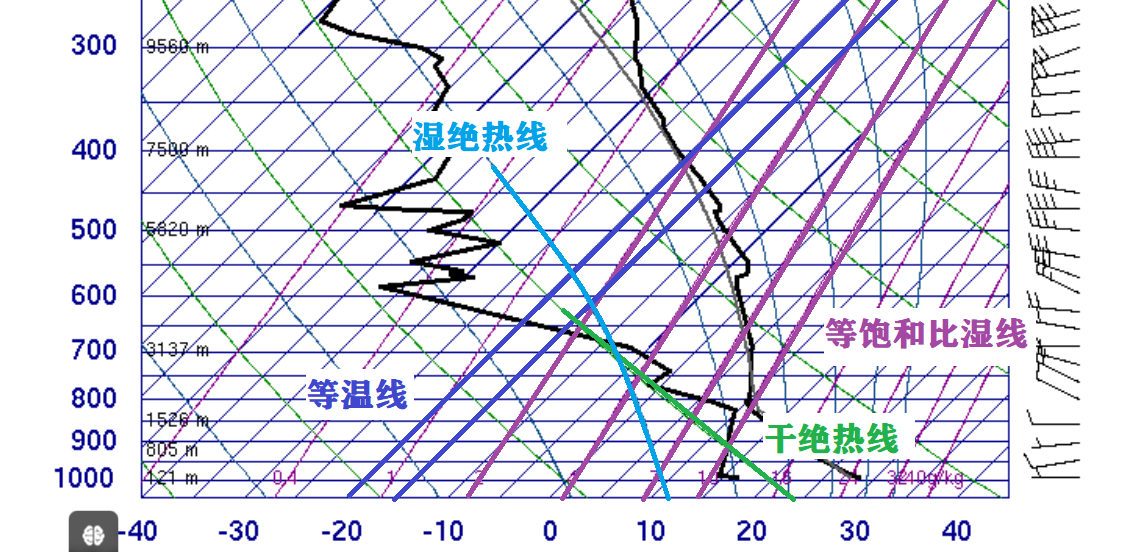
在 T-lnP 图上,等饱和比湿线是根据饱和比湿公式,并利用饱和水汽压的经验公式作积分而得到的。证明过程在这里就省略了。由于等温线就是等饱和水汽压线,而压强 p 随着纵坐标而减少,因此这组等饱和比湿线看起来像一组偏离等温线的近似直线,如下图所示,图中紫色线即为等饱和比湿线:

现在我们把已经接触过的四条线都标注在 T-lnP 图上:
7.4 相对湿度与绝对湿度
7.4.1 相对湿度
相对湿度(用 \(\mathrm{RH}\) 表示)就是空气中的实际水汽压与同温度下的饱和水汽压的比值,也可以指空气中实际水汽含量与同温度下时饱和水汽含量的比值,即:
相对湿度直接反映空气距离饱和的程度。当其接近 100% 时,表明当时空气接近于饱和。当水汽压不变时,气温升高,饱和水汽压增大,相对湿度会减小。
7.4.2 绝对湿度
绝对湿度(用 \(a\) 表示)是指给定体积空气中水汽的质量,定义式如下:
其中,\(m\) 为水汽质量,\(V\) 为空气体积。
绝对湿度不能直接测量,需根据气温和水汽压来推算,在应用上没有水汽压方便。
7.5 露点变化和抬升凝结高度
7.5.1 露点温度
在空气中水汽含量不变,气压一定下,使空气冷却达到饱和时的温度,称露点温度,简称露点(用 \(T_d\) 表示)。其单位与气温相同。当温度为 \(T\),压强为 \(p\) 时,相对湿度由下式给出:
在气压一定时,露点的高低只与空气中的水汽含量有关,水汽含量愈多,露点愈高,所以露点也是反映空气中水汽含量的物理量。
在实际大气中,空气经常处于未饱和状态,露点温度常比气温低(\(T_d < T\))。因此,根据 \(T\) 和 \(T_d\) 的差值,可以大致判断空气距离饱和的程度。
7.5.2 抬升凝结高度(LCL)
未饱和湿空气块被外力强迫抬升时,因为上升速度快,可以认为是绝热的,此时气块内的水汽压随着环境气压的减小而减小,与此对应,露点温度也降低。气块上升时的干绝热递减率远大于它的露点递减率,气块的温度和露点温度将逐渐接近,在某一高度达到饱和并发生凝结。这个湿空气块因绝热抬升而达到饱和的高度被称为抬升凝结高度(Lifting Condensation Level,LCL)。
因为水汽压 \(e\) 为露点 \(T_d\) 所对应的饱和水汽压,两者有函数关系,所以气块上升的露点变化可写为:
现在以 \(e\) 和 \(T_d\) 代替克拉珀龙-克劳修斯方程中的 \(e_s\) 和 \(T\) 有:
由水汽压的公式 \(e = \chi_w p\) 取对数,再对高度求导数得:
将上两式代入到露点变化的式子得:
若取 \(T_d = 280 \mathrm{K}\),\(T_v = 288 \mathrm{K}\),则 \(\frac{\mathrm{d} T_d}{\mathrm{d} z} = -0.0017 \mathrm{K/m} = -1.7 \mathrm{K/km}\)。因此,干绝热过程中露点以 \(1.7 \mathrm{K/km}\) 的变化率向上递减。但气块温度以 \(9.8 \mathrm{K/km}\) 递减,下降更快,在温度和露点温度相等的高度就会凝结。
令 \(T_0\) 和 \(T_{d0}\) 分别为地面温度和露点温度,所以有:
由以上两式可得抬升凝结高度的估算公式:
上式可估算对流云底的高度,不过由于地面的温度露点差 \(T_0 - T_{d0}\) 在一天中可变化几度,再加上气块垂直运动所做的绝热假定与实际情况有一定差距,这个公式有时与实际情况的差距很大。
7.6 两个例子理解湿度参数
7.6.1 往封闭空间加入水汽的例子
| 状态 | 空气总质量 | 水汽含量 | 比湿 | 温度 | 该温度下的饱和混合比 | 相对湿度 |
|---|---|---|---|---|---|---|
| 初始状态 | 1kg | 5g | 5g/kg | 25℃ | 20g/kg | 5/20 = 25% |
| 增加 5g 水汽 | 1kg | 10g | 10g/kg | 25℃ | 20g/kg | 10/20 = 50% |
| 增加 10g 水汽 | 1kg | 20g | 20g/kg | 25℃ | 20g/kg | 20/20 = 100% |
7.6.2 将封闭空间降温的例子
| 状态 | 空气总质量 | 水汽含量 | 比湿 | 温度 | 该温度下的饱和混合比 | 相对湿度 |
|---|---|---|---|---|---|---|
| 初始状态 | 1kg | 7g | 7g/kg | 20℃ | 14g/kg | 7/14 = 50% |
| 冷却到 10 ℃ | 1kg | 7g | 7g/kg | 10℃ | 7g/kg | 7/7 = 100% |
| 冷却到 0 ℃ | 1kg | 3.5g(凝结 3.5g 水) | 3.5g/kg | 0℃ | 3.5g/kg | 3.5/3.5 = 100% |