P3993 [BJOI2017] 同构 题解

Description

你有 \(n\) 个点，你可以在这 \(n\) 个点之间连无向边，两个点之间至多只能连一条边，也不允许连自环，问至多能连多少条边。

但这个问题的答案显然是 \(\frac{n(n-1)}{2}\) 条。所以有一个额外的限制，要求这个图不存在非平凡的自同构。

一个图 \(G\) 有非平凡的自同构定义为存在一个 \(1\) 到 \(n\) 的置换 \(p(1)\) 到 \(p(n)\) 满足对于所有点 \(u,v\)，\((u, v)\) 之间有边当且仅当 \((p(u), p(v))\) 之间有边，并且这个置换非平凡也就是存在一个点 \(u\) 使得 \(p(u) \ne u\)。

比如对于一个 \(5\) 个点的图 \((1,2),(2,3),(3,4),(4,5),(5,1),(1,3)\)，那么 \(p(1)=3\)，\(p(2)=2\)，\(p(3)=1\)，\(p(4)=5\)，\(p(5)=4\) 为这个图的一个非平凡的自同构。

你要回答一个 \(n\) 个点的无向简单的不存在非平凡自同构的图最多有多少条边，如果答案不存在，即不存在 \(n\) 个点满足条件的图，请输出 -1，否则输出答案对 \(10^9+7\) 取模的结果。

对于 \(100\%\) 的数据，\(1 \le n \le 10^{100}\)，\(1 \le T \le 10^4\)。

Solution

观察样例可以得到 \(n\leq 6\) 的答案，这里只考虑 \(n\geq 7\) 的情况。

容易发现对于一个图 \(G\) 合法，则 \(G\) 的补图 \(G'\) 也合法，所以只需要求出最少有多少条边即可。

手玩之后会发现对于每个合法方案，每个连通块一定不存在非平凡自同构且连通块两两不同构。

首先对于 \(n\geq 7\) 一定有解，构造如下：

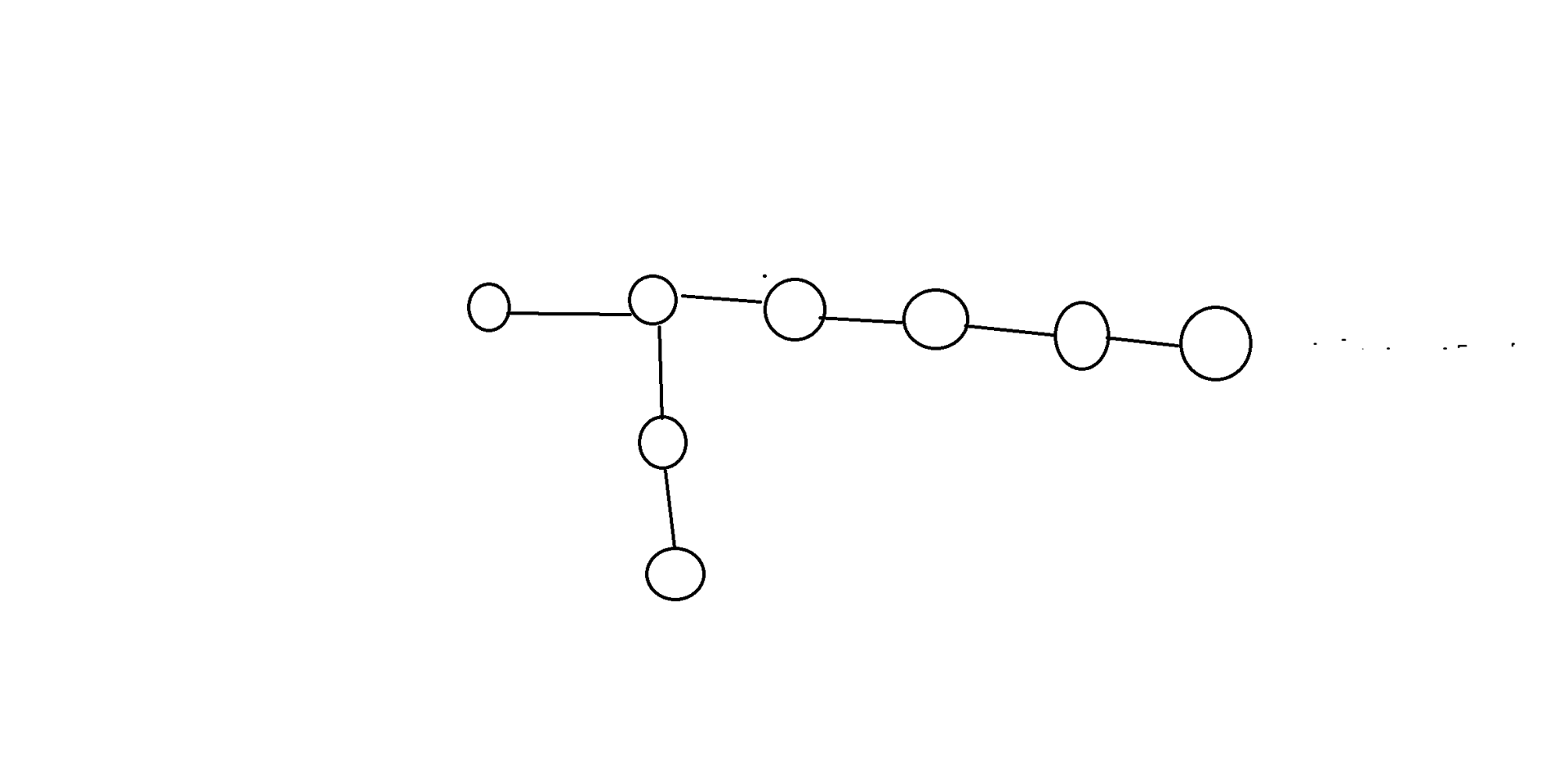
容易发现对于每个 \(n\)，最小的情况一定是个森林，证明就考虑如果只有 \(\leq 1\) 个树，则把方案改成一个 \(n\) 个点的树一定不劣。然后这时就有 \(\geq 2\) 个树了，则让点数最多的树和其它非树连通块的点删掉原先的边并连成一颗新树，这样一定合法且不劣。

所以只需要让树的个数最多即可。

容易发现肯定是先取点数小的树再取点数大的，剩下的点合并到最大的树一定合法。

考虑什么样的树是合法的。先固定根，对于每个点 \(x\) 的所有子树，一定是不同构的，如果对于所有的根都满足这个条件就一定合法。

有一个结论是：在判断树同构的时候，我们可以以重心为根做一遍树哈希（如果有两个就都做一遍），然后比较哈希值判断两棵树是否同构。

于是可以用重心来计算方案数可以避免算重。

设 \(f_n\) 表示 \(n\) 个点的无根树的个数，\(g_{n,m}\) 表示由大小 \(\leq n\) 的树组成大小为 \(m\) 的森林的方案数，\(h_n\) 表示 \(n\) 个点的有根树个数。

则：

\[\begin{aligned} h_n&=g_{n-1,n-1}\\ g_{n,m}&=\sum_{i=0}^{\left\lfloor\frac{m}{n}\right\rfloor}\binom{h_n}{i}g_{n-1,m-in}\\ f_n&=g_{\left\lfloor\frac{n-1}{2}\right\rfloor,n-1}+\left[2|n\right]\binom{h_{\frac{n}{2}}}{2} \end{aligned} \]

经计算，当 \(n=266\) 时 \(\sum{if_i}\) 已经 \(\geq 10^{100}\) 了。

时间复杂度：\(O(玄学)\)。

Code

#include <bits/stdc++.h>#define int int64_tnamespace BIGINT {
using ull = unsigned long long;
using bigint = __int128;
using bigbig = __int128;
struct bign {static const int block = 16;static const ull base = 10000000000000000;std::vector<ull> a;bign() : a(std::vector<ull>()) {}bign(ull x) {for (; x; x /= base) a.push_back(x % base);}bign(std::string s) {std::reverse(s.begin(), s.end());for (int i = 0; i < (int)s.length(); i += block) {int r = std::min((int)s.length(), i + block);ull x = 0;for (int j = r - 1; j >= i; j--) x = x * 10 + s[j] - 48;a.push_back(x);}}bign operator=(ull x) { return *this = bign(x); }bign operator=(std::string s) { return *this = bign(s); }void resize(int len) { a.assign(len, 0); }ull operator[](const int &x) const { return a[x]; }ull &operator[](const int &x) { return a[x]; }friend std::istream &operator>>(std::istream &in, bign &x) {std::string s;in >> s, x = s;return in;}friend std::ostream &operator<<(std::ostream &out, const bign &x) {if (x.a.empty())out << "0";else {ull ed = x.a.back();printf("%llu", ed);for (int i = x.a.size() - 2; ~i; i--) printf("%0*llu", block, x[i]);}return out;}bool operator<(const bign &x) const {if (a.size() != x.a.size()) return a.size() < x.a.size();for (int i = a.size() - 1; ~i; i--)if (a[i] ^ x[i]) return a[i] < x[i];return 0;}bool operator==(const bign &x) const {if (a.size() != x.a.size()) return 0;for (int i = 0; i < (int)a.size(); i++)if (a[i] ^ x[i]) return 0;return 1;}bool operator!=(const bign &x) const { return !(*this == x); }bool operator>(const bign &x) const { return x < *this; }bool operator<=(const bign &x) const {if (a.size() != x.a.size()) return a.size() < x.a.size();for (int i = a.size() - 1; ~i; i--)if (a[i] ^ x[i]) return a[i] < x[i];return 1;}bool operator>=(const bign &x) const { return x <= *this; }bign operator+=(const bign &x) {ull r = 0;for (int i = 0; i < (int)x.a.size() || r; i++) {if (i < (int)x.a.size()) r += x[i];if (i >= (int)a.size()) a.push_back(0);if ((a[i] += r) >= base)r = 1, a[i] -= base;elser = 0;}return *this;}bign operator+(const bign &x) const {bign t = *this;return t += x;}bign operator-=(const bign &x) {ull r = 0;for (int i = 0; i < (int)x.a.size() || r; i++) {if (i < (int)x.a.size()) r += x[i];if (a[i] >= r)a[i] -= r, r = 0;elsea[i] += base - r, r = 1;}for (; !a.empty() && !a.back();) a.pop_back();return *this;}bign operator-(const bign &x) const {bign t = *this;return t -= x;}bign operator-=(const ull &_x) {ull r = 0;ull x = _x;for (int i = 0; x || r; i++) {r += x % base, x /= base;if (a[i] >= r)a[i] -= r, r = 0;elsea[i] += base - r, r = 1;}for (; !a.empty() && !a.back();) a.pop_back();return *this;}bign operator-(const ull &x) const {bign t = *this;return t -= x;}friend void reduce(bign &a) {for (; !a.a.empty() && !a.a.back(); a.a.pop_back());}friend void split(const bign &a, bign &x, bign &y, int mid) {int len = std::min(mid, (int)a.a.size());y.resize(len);for (int i = 0; i < len; i++) y[i] = a[i];len = std::max<int>(0, (int)a.a.size() - mid);x.resize(len);for (int i = 0; i < len; i++) x[i] = a[mid + i];reduce(x), reduce(y);}friend bign mul(const bign &a, int x) {if (a.a.empty()) return bign();bign b;b.resize(a.a.size() + x);for (int i = a.a.size() - 1; ~i; i--) b[i + x] = a[i];return b;}bign operator*(const bign &x) const {if (a.size() <= 20 && x.a.size() <= 20) {int len = a.size() + x.a.size() + 1;std::vector<bigbig> t(a.size() + x.a.size() + 1);for (int i = 0; i < (int)a.size(); i++)for (int j = 0; j < (int)x.a.size(); j++) {int k = i + j;t[k] += (bigbig)a[i] * x[j], t[k + 1] += t[k] / base, t[k] %= base;}bign ans;ans.resize(len);for (int i = 0; i < (int)t.size(); i++) {if (i + 1 < (int)t.size()) t[i + 1] += t[i] / base;ans[i] = t[i] % base;}reduce(ans);return ans;}int mid = (std::max(a.size(), x.a.size()) + 1) / 2;bign A, B, C, D;split(*this, A, B, mid);split(x, C, D, mid);bign ac = A * C, bd = B * D, t = (A + B) * (C + D) - ac - bd;return mul(ac, mid * 2) + mul(t, mid) + bd;}bign operator*=(const bign &x) { return *this = *this * x; }bign operator*=(const int &x) {bigint r = 0;for (int i = 0; i < (int)a.size() || r; i++) {if (i >= (int)a.size()) a.push_back(0);r += x * (bigint)a[i], a[i] = r % base, r /= base;}return *this;}bign operator*(const int &x) const {bign t = *this;return t *= x;}bign operator*=(const ull &x) {bigint r = 0;for (int i = 0; i < (int)a.size() || r; i++) {if (i >= (int)a.size()) a.push_back(0);r += x * (bigint)a[i], a[i] = r % base, r /= base;}return *this;}bign operator*(const ull &x) const {bign t = *this;return t *= x;}bign operator/=(const ull &x) {bigint r = 0;for (int i = a.size() - 1; ~i; i--) {r = r * base + a[i];a[i] = r / x, r %= x;}for (; !a.empty() && !a.back();) a.pop_back();return *this;}bign operator/(const ull &x) const {bign t = *this;return t /= x;}friend bign qpow(const bign &_x, const ull &_y) {bign x(_x), ans(1);for (ull y = _y; y; y >>= 1, x *= x)if (y & 1) ans *= x;return ans;}ull trans() const {ull x = 0;for (int i = a.size() - 1; ~i; i--) x = x * base + a[i];return x;}ull operator%(const ull &x) const {ull res = 0;for (int i = a.size() - 1; ~i; i--) {res = ((bigbig)res * base + a[i]) % x;}return res;}
};
}  // namespace BIGINTusing BIGINT::bign;using i128 = __int128_t;const int kMaxN = 270, kMod = 1e9 + 7;bign f[kMaxN], g[kMaxN][kMaxN], h[kMaxN];constexpr int qpow(int bs, int64_t idx = kMod - 2) {int ret = 1;for (; idx; idx >>= 1, bs = (int64_t)bs * bs % kMod)if (idx & 1) ret = (int64_t)ret * bs % kMod;return ret;
}inline int add(int x, int y) { return (x + y >= kMod ? x + y - kMod : x + y); }
inline int sub(int x, int y) { return (x >= y ? x - y : x - y + kMod); }
inline void inc(int &x, int y) { (x += y) >= kMod ? x -= kMod : x; }
inline void dec(int &x, int y) { (x -= y) < 0 ? x += kMod : x; }bign C(bign n, int m) {static bool vis[kMaxN];if (n < m) return 0;bign ret = 1;memset(vis, 0, sizeof(vis));for (bign i = n; i > n - m; i = i - 1) {ret *= i;for (int j = 1; j <= m; ++j)if (!vis[j] && ret % j == 0) ret /= j, vis[j] = 1;}return ret;
}void prework() {g[0][0] = 1;for (int i = 1; i <= 266; ++i) {h[i] = g[i - 1][i - 1];if (i & 1)f[i] = g[(i - 1) / 2][i - 1];elsef[i] = g[i / 2 - 1][i - 1] + C(h[i / 2], 2);for (int j = 0; j <= 266; ++j) {for (int k = 0; k <= j / i; ++k)g[i][j] += C(h[i], k) * g[i - 1][j - i * k];}}
}int solve(bign n) {if (n == 1)return 0;else if (n <= 5)return -1;else if (n == 6)return 9;int _n = n % kMod, ans = (1ll * _n * (_n - 1) / 2 % kMod - _n + kMod) % kMod;for (int i = 1; i <= 266; ++i) {if (n > (bign)i * f[i]) {n -= (bign)i * f[i], inc(ans, f[i] % kMod);} else {inc(ans, (n / i) % kMod);break;}}return ans;
}void dickdreamer() {bign n;std::cin >> n;std::cout << solve(n) << '\n';
}int32_t main() {
#ifdef ORZXKRfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifint T = 1;std::cin >> T;prework();while (T--) dickdreamer();// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";return 0;
}