LCA
之前学废了,回来补。
倍增版
首先是最常见的倍增版子,思路好理解,按倍增记录 \(father\),然后同时往上跳。
注意最后跳到的是那个 \(x \ne y\) 的,也就是 \(lca\) 的儿子,所以最后要返回父亲。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m,rt;
int head[N],tot;
struct E{int u,v;} e[N<<1];
void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dep[N],fa[30][N];
void dfs(int u)
{for(int i=1;i<=25;i++)fa[i][u]=fa[i-1][fa[i-1][u]];for(int i=head[u];i;i=e[i].u){int v=e[i].v;if(dep[v]) continue;dep[v]=dep[u]+1; fa[0][v]=u;dfs(v);}
}
int lca(int x,int y)
{if(dep[x]<dep[y]) swap(x,y);for(int i=25;i>=0;i--) if(dep[fa[i][x]]>=dep[y]) x=fa[i][x];if(x==y) return x;for(int i=25;i>=0;i--) if(fa[i][x]!=fa[i][y]) x=fa[i][x],y=fa[i][y];return fa[0][x];
}
int main()
{scanf("%d%d%d",&n,&m,&rt);for(int i=2;i<=n;i++){int x,y; scanf("%d%d",&x,&y);add(x,y); add(y,x);}dfs(dep[rt]=1);//!!!while(m--){int x,y; scanf("%d%d",&x,&y);printf("%d\n",lca(x,y));}return 0;
}
DFS 序版
原博客
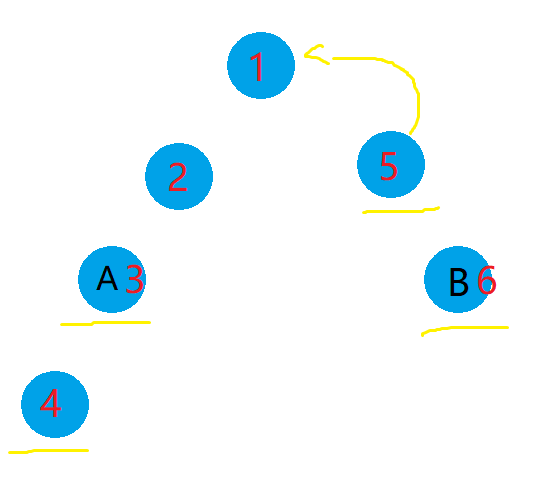
我们记录每个点的 \(dfn\) 时间戳和 dfs 序。
应用的性质是 \(lca\) 的 dfs 序不会出现在 \(u\) 和 \(v\) 之间出现。并且是在它们之前出现。
其中 dfs 序体现在 dfs 遍历时维护的 \(st\),也就是记录父亲。
最终 \(st[i][u]\) 表示的是以 \(u\) 的时间戳为起点,在dfs序上向后延长 \(2^i\) 位的深度最小值的节点的父亲,也就是 \(dfn\) 最小节点。
这里很神奇的是查询能直接查到 \(lca\),因为我们查询的是 \([dfn_u,dfn_v]\) 这段 \(dfs\) 序上的父亲时间戳最小值显然这个点一定就是 \(lca\)。
(挂张图)
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m,rt,dfn[N],num,st[20][N];
int head[N],tot;
struct E{int u,v;} e[N<<1];
void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int get(int x,int y) {return dfn[x]<dfn[y]?x:y;}
void dfs(int u,int fa)
{dfn[u]=++num; st[0][num]=fa;for(int i=head[u];i;i=e[i].u){int v=e[i].v;if(v!=fa) dfs(v,u);}
}
int lca(int x,int y)
{if(x==y) return x;x=dfn[x]; y=dfn[y];if(x>y) swap(x,y);int d=__lg(y-x);return get(st[d][x+1],st[d][y-(1<<d)+1]);
}
int main()
{scanf("%d%d%d",&n,&m,&rt);for(int i=2;i<=n;i++){int x,y; scanf("%d%d",&x,&y);add(x,y); add(y,x);}dfs(rt,0);for(int i=1;i<=__lg(n);i++)for(int j=1;j+(1<<i)-1<=n;j++)st[i][j]=get(st[i-1][j],st[i-1][j+(1<<i-1)]);while(m--){int x,y; scanf("%d%d",&x,&y);printf("%d\n",lca(x,y));}return 0;
}
树链剖分版
划分轻重链后往上跳,直到跳到同一条链上,其实就是借助了树剖的 dfs,亲民。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m,rt;
int head[N],tot;
struct E{int u,v;} e[N<<1];
void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}int sz[N],dep[N],fa[N],son[N],top[N];void dfs1(int u,int f)
{fa[u]=f; dep[u]=dep[f]+1; sz[u]=1; son[u]=-1;for(int i=head[u];i;i=e[i].u){int v=e[i].v;if(v==f) continue;dfs1(v,u);sz[u]+=sz[v];if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;}
}
void dfs2(int u,int t)
{top[u]=t;if(son[u]==-1) return ;dfs2(son[u],t);for(int i=head[u];i;i=e[i].u){int v=e[i].v;if(v!=fa[u]&&v!=son[u]) dfs2(v,v);}
}
int lca(int x,int y)
{while(top[x]!=top[y]){if(dep[top[x]]>=dep[top[y]]) x=fa[top[x]];else y=fa[top[y]];}return dep[x]<dep[y]?x:y;
}
int main()
{scanf("%d%d%d",&n,&m,&rt);for(int i=2;i<=n;i++){int x,y; scanf("%d%d",&x,&y);add(x,y); add(y,x);}dfs1(rt,0); dfs2(rt,rt);while(m--){int x,y; scanf("%d%d",&x,&y);printf("%d\n",lca(x,y));}return 0;
}
写在最后
虽然原博列举了很多 dfs 序 LCA 的优点,但是缺点也有一点点吧。
倍增方法可以处理 k 级祖先,这在一些树上跳的题目中很重要。
树剖可以顺便求出 lca,用途也比较广。
dfs 序码量较短,但是不太好想。而且用途比较单一。
而且好像除了 dfs 序版以外都很好理解???