\(一\) \(数据结构\)
\(1\) \(链表\)
\(1.0\) \(介绍\)
链表分为单向链表和双向链表
单向链表即当前链表只指向下一个元素
双向链表即对于每个元素,记录其前面一个元素,也记录其后面一个元
素。
链表不建议使用 STL 的某些元素进行替代,手写链表更为方便。
\(1.1\) \(单向链表\)
\(1.1.1\) \(介绍\)
维护每个元素编号,然后维护 nx 指针,表示当前元素的下
一个元素是谁加入和删除都是方便的。
\(1.1.2\) \(实现\)
//插入一个元素
void ins(int x,int y){int to = nx[x];nx[x] = y;nx[y] = to;
}//删除一个元素
void erase(int x){int to = nx[x];nx[x] = nx[to];
} \(1.1.3\) \(例题\)
luogu B3631 单向链表
点击查看代码
\(1.1.4\) \(前向星\)
本质上前项星是由多个单项链表组成,维护链头数组,然后可以支持每
个点加边。
struct node {int next;int to;
}e[N*2];
int cnt,h[N];
void add(int x,int y){cnt++;e[cnt] = {h[x],y};h[x] = cnt;
}
void dfs(int x){for (int i = h[x];i;i = e[i].next)dfs(e[i].to,x);
}
luogu p3916 图的遍历
点击查看代码(这份代码只能的60分)
using namespace std;#define ll long longconst int N = 1e5 + 5;int n,m;struct node{int next,to;
}e[N >> 1];int cnt,h[N];void add(int x,int y){cnt ++;e[cnt] = {h[x],y};h[x] = cnt;
}int ans[N],id;void dfs(int x){if(!ans[x]) ans[x] = id;else return ;for (int i = h[x];i;i = e[i].next)dfs(e[i].to);
}int main(){cin >> n >> m;for (int i = 1;i <= m;i ++){int a,b;cin >> a >> b;add(b,a);}for (int i = n;i >= 1;i --) id = i,dfs(i);for (int i = 1;i <= n;i ++) cout << ans[i] << " ";puts("");return 0;
}\(1.2\) \(双向链表\)
\(1.2.1\) \(介绍\)
每个元素维护前驱 pr 和后继 nx 两个数组,可以实现动态增删的操作
\(1.2.2\) \(实现\)
void ins(int x,int y){int to = nx[x];nx[x] = x;pr[to] = y;pr[y] = x;nx[y] = to;
}void era(int x){int L = pr[x],R = nx[x];nx[L] = R,pr[R] = L;
}\(2\) \(栈\)
\(2.0\) \(介绍\)
一种结构,维护一个序列,每次从末端加入元素,然后末端弹出元素。
具体维护:使用一个数组,维护一个 tp 指针进行处理
\(2.1\) \(维护\)
手写栈:
int stk[N],tp;
void push(int x){stk[++tp] = x;
}
void top(){return stk[tp];
}
void pop(){tp--;
}STL栈:
stack<int>stk;
stk.push(1);
stk.pop();
cout << stk.top() << "\n";
cout << stk.size() << "\n";
\(2.2\) \(例题\)
luogu p3618 【模板】栈
\(2.3\) \(单调栈\)
\(2.3.1\) \(介绍\)
本质上是用栈维护了单调的结构
\(2.3.1\) \(例题\)
luogu p5788 【模板】单调栈
从后往前枚举,栈内维护单调的下标,满足这些下标的值是递减的,id
也是递减的,由于满足单调的过程,我们称为单调栈。
关键性质在于保留对当前状态最优的信息。
\(3\) \(队列\)
\(3.0\) \(介绍\)
一种结构,维护一个序列,每次从末端加入元素,然后前端弹出元素。
具体维护,用一个数组,维护前端后端指针,维护加入删除。
\(3.1\) \(实现\)
手写:
int q[N],l,r;
void push(int x){q[++r] = x;
}
int front(){return q[1];
}
void pop(){l++;
}
STL:
queue<int>q;
q.push(1);
q.pop();
cout<<q.front()<<"\n";
cout<<q.size()<<"\n";
\(3.2\) \(例题\)
luogu B3616 【模板】队列
\(3.3\) \(单调队列\)
类比与单调栈,我们也有单调队列,满足这个队列中,(比如求最大值)
权值是递减的,但是 id 是递增的,有单调性质。
关键性质同样是保留对于当前而言更优的一个信息。
为什么权值递减?因为我们要求目前最大值,为什么 id 递增?我们有
id 大于某个位置的限制。

\(4\) \(堆\)
\(4.1\) \(介绍\)
一种结构,维护一个序列,每次加入一个元素,询问当前序列中最小的
元素,然后删除最小元素。
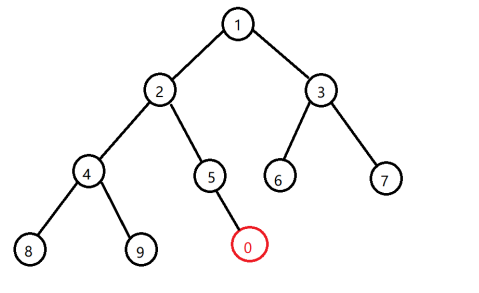
具体维护,我们一般维护的称为二叉堆,即维护一个结构,支持上述处
理过程。
每个节点 \(i\) 储存一个权值,左儿子是 \(2 ∗ i\),右儿子是 \(2 ∗ i + 1\)。
\(4.2\) \(实现\)


\(4.3\) \(例题\)
luogu B3616
\(4.4\) \(对顶堆\)
一个序列,我们每次加入一个元素,或者进行询问。
维护一个初始指针 i=0,每次询问的时候将 i=i+1 然后询问第 i 小的值
是多少。
例题
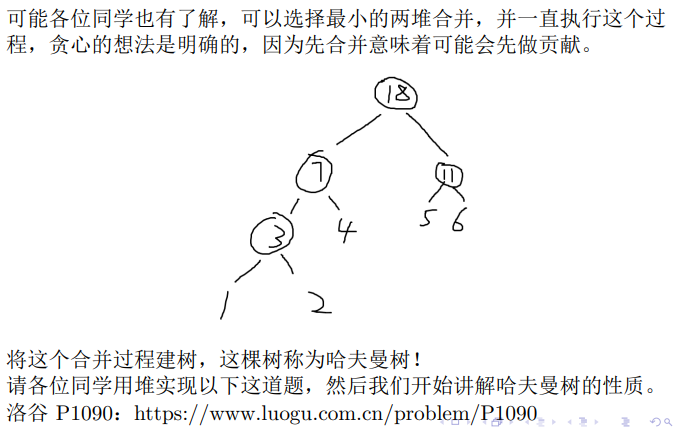
\(5\) \(哈夫曼树\)
\(5.1\) \(例题引入\)

\(5.2\) \(详解\)

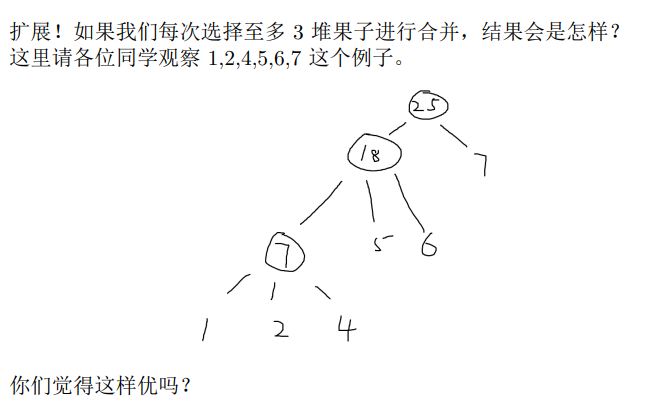

\(5.3\) \(例题\)
luogu p2168 荷马史诗
注意到,没有前缀包含关系完全对应了哈夫曼编码,而我们最优化次数
正好是哈夫曼树的最小的贡献!
所以我们建立扩展的 k 叉哈夫曼树即可得到答案。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read()
{char c;int w=1;while((c=getchar())>'9'||c<'0')if(c=='-')w=-1;int ans=c-'0';while((c=getchar())>='0'&&c<='9')ans=(ans<<1)+(ans<<3)+c-'0';return ans*w;
}
priority_queue<pair<int,int> >q;
int a[5000005];
int n;
int k;
signed main(){n=read();k=read();for(int i=1;i<=n;i++){a[i]=read();q.push(make_pair(-a[i],-1));}while((n-1)%(k-1))n++,q.push(make_pair(0,-1));int anss=0;for(int i=1;i<=(n-1)/(k-1);i++){int ans=0;int maxx=0;for(int j=1;j<=k;j++){ans+=(-q.top().first);maxx=max(maxx,-q.top().second);q.pop();}anss+=ans;q.push(make_pair(-ans,-maxx-1));}cout<<anss<<endl<<-q.top().second-1<<endl;return 0;
}\(二\) \(STL、差分、前缀和\)
\(1\) \(STL\)
STL 是 C++ 标准库的一部分,包含了很多数据结构和算法,我们可以
直接调用这些函数来解决问题。
比如说,我们可以直接调用 vector 来解决动态开数组的问题,调用 set
来解决集合(有序数组)的问题。
我们随着代码一起来理解一下这些 STL。
点击查看STL
#include<bits/stdc++.h>
#define ll long long
#define dd double
#define ull unsigned ll
#define LL __int128
#define siz(A) ((int)A.size())
using namespace std;
char gc(){static char buf[1<<16],*s,*t;if(s==t){t=(s=buf)+fread(buf,1,1<<16,stdin);if(s==t)return EOF;}return *s++;}
//#define getchar gc
ll read(){char c;ll w=1;while((c=getchar())>'9'||c<'0')if(c=='-')w=-1;ll ans=c-'0';while((c=getchar())>='0'&&c<='9')ans=(ans<<1)+(ans<<3)+c-'0';return ans*w;
}
void pc(char c,int op)
{static char buf[1<<16],*s=buf,*t=(buf+(1<<16));(op||((*s++=c)&&(s==t)))&&(fwrite(buf,1,s-buf,stdout),s=buf);
}
void wt(int x)
{if(x>9)wt(x/10);pc('0'+x%10,0);
}
void wts(int x,char op)
{if(x<0)pc('-',0),x=-x;wt(x),pc(op,0);
}
namespace vec
{vector<int>v;void test(){vector<int>A(5);vector<int>B(5,3);vector<int>C={1,2,3};for(vector<int>::iterator it=A.begin();it!=A.end();it++)cout<<*it<<" ";puts("");for(auto it:B)cout<<it<<" ";puts("");for(int i=0;i<(int)C.size();i++)cout<<C[i]<<" ";puts("");int n=read();v.resize(100);cout<<(int)v.size()<<"\n";//unsignedcout<<(int)v.capacity()<<"\n";for(int i=1;i<=n;i++)v.push_back(i);cout<<(int)v.size()<<"\n";//unsignedcout<<(int)v.capacity()<<"\n";v.shrink_to_fit();cout<<(int)v.capacity()<<"\n";v.push_back(2);cout<<(int)v.size()<<"\n";cout<<(int)v.capacity()<<"\n";v.clear();cout<<(int)v.capacity()<<"\n";vector<int>().swap(v);cout<<(int)v.capacity()<<"\n";}
}
namespace basic
{basic_string<int>v;void test(){int n=read();v.resize(100);cout<<(int)v.size()<<"\n";//unsignedcout<<(int)v.capacity()<<"\n";for(int i=1;i<=n;i++)v.push_back(i);cout<<(int)v.size()<<"\n";//unsignedcout<<(int)v.capacity()<<"\n";v.shrink_to_fit();cout<<(int)v.capacity()<<"\n";v.push_back(2);cout<<(int)v.size()<<"\n";cout<<(int)v.capacity()<<"\n";v.clear();cout<<(int)v.capacity()<<"\n";basic_string<int>().swap(v);cout<<(int)v.capacity()<<"\n";basic_string<int>A={2,3,4};basic_string<int>B={2,3,4};for(auto it:A)cout<<it<<" ";puts("");A=A+B;for(auto it:A)cout<<it<<" ";puts("");//string cout<<A.find({4,2})<<"\n"; }
}namespace se
{set<int>A;multiset<int>B;void test(){for(int i=1;i<=3;i++){A.insert(i);//pair <bool,iterator>A.insert(i);B.insert(i);//指针 iterator B.insert(i);}for(auto it:A)cout<<it<<" ";puts("");for(auto it:B)cout<<it<<" ";puts("");multiset<int>::iterator x=B.lower_bound(0);multiset<int>::iterator y=B.find(2);B.erase(x);for(auto it:B)cout<<it<<" ";puts("");B.erase(3);for(auto it:B)cout<<it<<" ";puts("");cout<<(int)B.size()<<"\n";cout<<(int)B.count(2)<<"\n";A.clear(),B.clear();//不能数组下标访问。 }
}namespace ma
{map<int,int>A;unordered_map<int,int>B;void test(){for(int i=1;i<=3;i++)A[i]=i-1,B[i]=i-1;for(auto it:A)cout<<it.first<<" "<<it.second<<"\n";puts("");// for(auto it:B)cout<<it<<" ";
// puts("");auto it=A.find(2);//key cout<<A[4]<<"\n";A.clear(),B.clear();}
}namespace bit
{bitset<10>bit,bb;void test(){bit[5]=1;cout<<bit<<"\n";bit.flip();bit<<=3;cout<<bit<<"\n";bb[1]=1;bb[4]=1;cout<<bb<<"\n";bit^=bb;cout<<bit<<"\n";int A=bit._Find_first();cout<<A<<"\n";cout<<bit._Find_next(A)<<"\n";}
}int main(){vec::test();basic::test();se::test();ma::test();bit::test();pair<int,int>A;array<int,2>B;// stack
// queue
// priority_queue
// sort();
// merge();
// nth_element();
// next_permutation();
// swap();vector<int>B=A;sort(A.begin(),A.end());A.resize(unique(A.begin(),A.end())-A.begin());for(auto it:B)cout<<it<<" ";puts("");for(int i=0;i<(int)B.size();i++)B[i]=lower_bound(A.begin(),A.end(),B[i])-A.begin();for(auto it:B)cout<<it<<" ";puts("");pc('1',1);return 0;
}
\(2\) \(差分\)
\(2.1\) \(差分前缀和\)
是一个很简单的算法,我们可以用来解决一些区间的问题
\(2.2\) \(差分\)
若当前我们每次形如修改一个区间,使得区间加上一个值,最后我们需
要求出修改之后的数组我们应该怎么办呢?
我们可以用差分的方式,即对于每个区间 [l, r],我们让 al 加上 v,ar+1
减去 v。
\(3\) \(ST表\)
倍增在 OI 种是一个重要的思想,今天我们来介绍一下倍增思想的一个
应用:ST 表。
我们可以用 ST 表来解决一些区间的问题,最为经典的问题是,解决区
间极值的问题。
简要介绍一下 ST 表的原理:
给定一个长度为 N 的数列,和 M 次询问,求出每一次询问的区间内数
字的最大值。