blog。今天在 XDFZ 听 ljy 讲的串串(?)题,瞎写写就混了个最优解,来发个题解(
注意到树的形态不变,所以可以记录兄弟间的编号 rank。每个点就可以表示为若干 rank 构成的路径,例如下图:
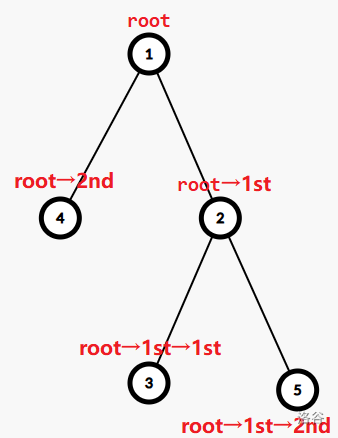
然后将每个点的这个路径压成 hash,记为 \(H_i\),并丢进 map 里。
假设从 \(x\) 开始,可以完全遍历完 \(a_{l\sim w}\),那么等价于存在一条 rank 路径为 \(H_i\to a_l\to a_{l+1}\to\cdots\to a_w\)。
发现这是可二分的,即:如果存在 \(a_{l\sim w}\) 的路径,那么也必定存在 \(a_{l\sim l}, a_{l\sim (l+1)}, \cdots, a_{l\sim (w-1)}, a_{l\sim w}\) 的路径。
所以直接二分出最小的 \(w\) 使得 \(a_{l\sim w}\) 的 rank 路径存在即可。
这个问题只需要做到维护 \(\forall a_{l\sim r}\) 的 hash 值,线段树 / 树状数组都行,套个二分就有 \(O(\log^2)\) 做法了。
注意到我们可以线段树上二分,这样就做到了 \(O(\log)\)。代码并不难写。
代码是最优解的一发,会有一点点抽象,不过应该看得懂 /cy。
贺了 OIWiki 的 hash 表,也可以用 unordered_map 实现,不过前者会快 4s。
code,时间复杂度 \(O(n+m\log m)\)。



![[智能网联汽车] CAN Log 文件 - ASC文件格式 [转]](https://blog-static.cnblogs.com/files/johnnyzen/cnblogs-qq-group-qrcode.gif?t=1679679148)