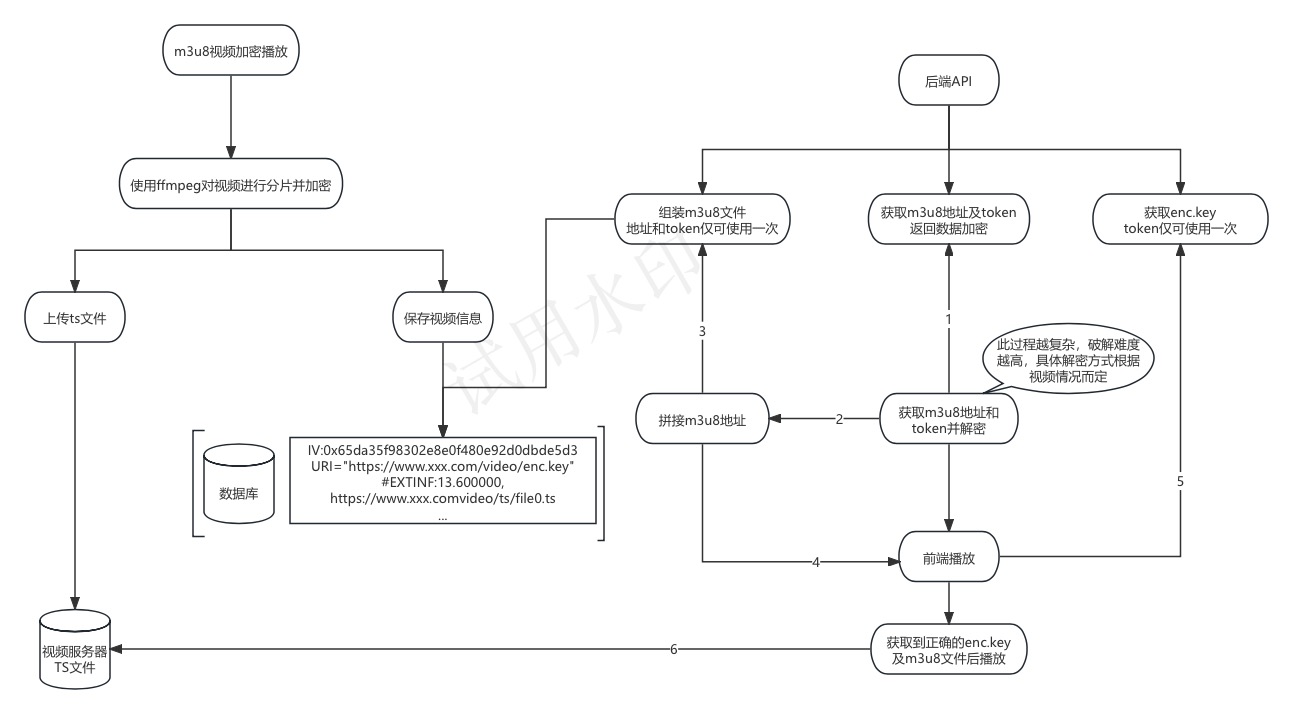
连通性相关

news/2024/11/15 18:21:03/文章来源:https://www.cnblogs.com/wshcl/p/18306858/SCC

连通性相关

强连通分量

强连通分量（SCC）：极大的强连通子图。

Tarjan 算法

维护一个栈存储搜索到的还未确定强连通分量的点，定义：

  • \(dfn_u\) ：节点 \(u\) 被搜索的次序。
  • \(low_u\) ：\(u\) 子树中能回溯到的最小的 \(dfn\) 。

不难得到：

  • 一个点子树内的 \(dfn\) 大于该点的 \(dfn\) 。
  • 从根开始的路径上的 \(dfn\) 递增，\(low\) 非降。

对于 \(u\) 的出点 \(v\) ，考虑

  • \(v\) 未被访问过：继续 dfs ，并用 \(low_v\) 更新 \(low_u\) 。因为存在 \(u \to v\) ，所以 \(v\) 可以直接回溯到已在栈中的点 \(u\) 一定可以回溯到。

  • \(v\) 被访问过

    • 已在栈中：根据 \(low\) 的定义，用 \(dfn_v\) 更新 \(low_u\) 。

    • 不在栈中：说明 \(v\) 已搜索完毕，其所在的连通分量已被处理，不用管它。

对于一个强连通分量，不难发现只有一个 \(u\) 满足 \(dfn_u = low_u\) ，其一定是这个强连通分量的根。

因此回溯过程中，若 \(dfn_u = low_u\) ，则新增一个强连通分量。

void Tarjan(int u) {dfn[u] = low[u] = ++dfstime, sta[++top] = u;for (int v : G.e[u]) {if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (!leader[v])low[u] = min(low[u], dfn[v]);}if (dfn[u] == low[u]) {++scc;while (sta[top] != u)leader[sta[top--]] = scc;leader[sta[top--]] = scc;}
}

应用

对于一张有向图，其可能存在环。可以将每个强连通分量分别缩成一个点，这个图就会变成一张 DAG，可能会便于处理。

Kosaraju 算法

  • 第一次 dfs：遍历所有点并在回溯时入栈。
  • 第二次 dfs：在反图上依次从栈顶开始 dfs ，此时遍历到的点集就是一个强连通分量。

时间复杂度 \(O(n + m)\) 。

void dfs1(int u) {vis[u] = true;for (int v : G.e[u])if (!vis[v])dfs1(v);sta.emplace(u);
}void dfs2(int u) {leader[u] = scc;for (int v : rG.e[u])if (!leader[v])dfs2(v);
}inline void kosaraju() {for (int i = 1; i <= n; ++i)if (!vis[i])dfs1(i);for (; !sta.empty(); sta.pop())if (!leader[sta.top()])++scc, dfs(sta.top());
}

用 bitset 优化可以做到 \(O(n^2)\) 的复杂度，某些题目有奇效。

void dfs1(int u) {vis.set(u);bitset<N> now = ~vis & e1[u];while (now.any())dfs1(now._Find_first()), now &= ~vis;sta.push(u);
}void dfs2(int u) {vis.set(u), leader[u] = scc;bitset<N> now = ~vis & e2[u];while (now.any())dfs2(now._Find_first()), now &= ~vis;
}inline void kosaraju() {vis.reset();for (int i = 1; i <= n; ++i)if (!vis.test(i))dfs1(i);vis.reset();for (; !sta.empty(); sta.pop())if (!vis.test(sta.top()))++scc, dfs(sta.top());
}

应用

BZOJ5218 省队十连测 友好城市

给出一张有向图，\(q\) 次询问仅保留编号属于 \([l_i, r_i]\) 的边时有多少无序对城市满足可以两两到达。

\(n \leq 150, m \leq 3 \times 10^5, q \leq 5 \times 10^4\)

注意到 \(n\) 很小，使用 kosaraju 配合莫队即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 1.5e2 + 7, M = 3e5 + 7, Q = 5e4 + 7;struct Edge {int u, v;
} E[M];struct Query {int l, r, *ans, bid;inline bool operator < (const Query &rhs) const {return bid == rhs.bid ? (bid & 1 ? r < rhs.r : r > rhs.r) : bid < rhs.bid;}
} qry[Q];bitset<N> e1[N], e2[N];
bitset<N> vis;
stack<int> sta;int cnt1[N][N], cnt2[N][N], ans[Q];int n, m, q, block, scc;template <class T = int>
inline T read() {char c = getchar();bool sign = c == '-';while (c < '0' || c > '9')c = getchar(), sign |= c == '-';T x = 0;while ('0' <= c && c <= '9')x = (x << 1) + (x << 3) + (c & 15), c = getchar();return sign ? (~x + 1) : x;
}inline void Add(int x) {int u = E[x].u, v = E[x].v;if (!cnt1[u][v])e1[u][v] = true;if (!cnt2[v][u])e2[v][u] = true;++cnt1[u][v], ++cnt2[v][u];
}inline void Del(int x) {int u = E[x].u, v = E[x].v;--cnt1[u][v], --cnt2[v][u];if (!cnt1[u][v])e1[u][v] = false;if (!cnt2[v][u])e2[v][u] = false;
}void dfs1(int u) {vis.set(u);bitset<N> now = ~vis & e1[u];while (now.any())dfs1(now._Find_first()), now &= ~vis;sta.push(u);
}int dfs2(int u) {vis.set(u);bitset<N> now = ~vis & e2[u];int siz = 1;while (now.any())siz += dfs2(now._Find_first()), now &= ~vis;return siz;
}inline int kosaraju() {vis.reset(), scc = 0;int res = 0;for (int i = 1; i <= n; ++i)if (!vis.test(i))dfs1(i);vis.reset();for (; !sta.empty(); sta.pop())if (!vis.test(sta.top())) {int siz = dfs2(sta.top());res += siz * (siz - 1) / 2;}return res;
}signed main() {n = read(), m = read(), q = read();block = sqrt(m);for (int i = 1; i <= m; ++i)E[i].u = read(), E[i].v = read();for (int i = 1; i <= q; ++i)qry[i].l = read(), qry[i].r = read(), qry[i].bid = qry[i].l / block, qry[i].ans = ans + i;sort(qry + 1, qry + 1 + q);for (int i = 1, l = 1, r = 0; i <= q; ++i) {while (l > qry[i].l)Add(--l);while (r < qry[i].r)Add(++r);while (l < qry[i].l)Del(l++);while (r > qry[i].r)Del(r--);*qry[i].ans = kosaraju();}for (int i = 1; i <= q; ++i)printf("%d\n", ans[i]);return 0;
}

应用

CF1515G Phoenix and Odometers

给定一张带边权的有向图，\(q\) 次询问，每次给定 \(v, s, t\) ，询问时候存在一条经过 \(v\) 的回路满足长度与 \(-s\) 在模 \(t\) 意义下同余。

\(n, m, q \leq 2 \times 10^5\) 。

首先不难发现每个 SCC 的答案是一致的，且不同 SCC 之间相互独立，故考虑对于每个 SCC 分开计算。

假设经过 \(u\) 有两个长度为 \(a\) 和 \(b\) 的环，那么就相当于找两个非负整数 \(x\) 和 \(y\)，使得 \(ax + by = w\)，其中 \(w\) 为题中的路径长，根据裴蜀定理得到上述方程成立当且仅当 \(\gcd(a, b) \mid w\) 。

考虑如何求出经过点 \(u\) 的所有环长度的 \(\gcd\) 。通过分析发现，所有的非树边 \(u \to v\) 对答案的贡献都是 \(dis_u + w - dis_v\) 。于是搜索时顺便记录贡献即可。

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 2e5 + 7;struct Graph {vector<pair<int, int> > e[N];inline void insert(const int u, const int v, const int w) {e[u].emplace_back(v, w);}
} G;ll dis[N], g[N];
int dfn[N], low[N], sta[N], leader[N];
bool vis[N];int n, m, q, dfstime, top, scc;template <class T = int>
inline T read() {char c = getchar();bool sign = (c == '-');while (c < '0' || c > '9')c = getchar(), sign |= (c == '-');T x = 0;while ('0' <= c && c <= '9')x = (x << 1) + (x << 3) + (c & 15), c = getchar();return sign ? (~x + 1) : x;
}inline ll gcd(ll a, ll b) {if (!a || !b)return a | b;while (a ^= b ^= a ^= b %= a);return b;
}void Tarjan(int u) {dfn[u] = low[u] = ++dfstime, sta[++top] = u;for (auto it : G.e[u]) {int v = it.first;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (!leader[v])low[u] = min(low[u], dfn[v]);}if (low[u] == dfn[u]) {++scc;while (sta[top] != u)leader[sta[top--]] = scc;leader[sta[top--]] = scc;}
}void dfs(int u, int cur) {vis[u] = true;for (auto it : G.e[u]) {int v = it.first, w = it.second;if (leader[v] != cur)continue;if (!vis[v])dis[v] = dis[u] + w, dfs(v, cur);elseg[cur] = gcd(g[cur], abs(dis[u] - dis[v] + w));}
}signed main() {n = read(), m = read();for (int i = 1; i <= m; ++i) {int u = read(), v = read(), w = read();G.insert(u, v, w);}for (int i = 1; i <= n; ++i)if (!dfn[i])Tarjan(i);for (int i = 1; i <= n; ++i)if (!vis[i])dfs(i, leader[i]);q = read();while (q--) {int x = read(), s = read(), t = read();if (g[leader[x]])puts(s % gcd(g[leader[x]], t) ? "NO" : "YES");elseputs(s ? "NO" : "YES");}return 0;
}

2-SAT

2-SAT 问题：给定一串布尔变量，每个变量只能为真或假。要求对这些变量进行赋值，满足布尔方程。

实现

构造状态

点的状态：将点 \(u\)​​ 拆分成 \(u0,u1\)​ 两个点，分别表示 \(u\)​ 点为假、真。

边的状态：若连的边为 \(u \to v\) ，就表示选择 \(u\) 就必须选 \(v\) 。

判断有无解

由所构造的状态可知，对于图中的每一个强连通分量，如果选择了其中任意一个点，那就意味着这个强连通分量中的所有点都要选。显然 \(x0,x1\)​​ 不可以同时选，由此可判断有无解。

方案输出

由连边的方式可以得知，我们对于每个点的两种状态，选择拓扑序大的，舍弃掉另一个。

注意到用 Tarjan 求得的强连通分量编号就是反拓扑序，于是选择强连通分量编号较小的点即可。

如果要求字典序最小，就深搜枚举点 \(1 \to 2n\) ，贪心选取。

P4782 【模板】2-SAT 问题

#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 7;vector<int> e[N];
stack<int> sta;int dfn[N], low[N], leader[N];int n, m, dfstime, cnt;inline void AddEdge(int u, int v) { e[u].push_back(v); 
}inline void Tarjan(int u) {dfn[u] = low[u] = ++dfstime;sta.push(u);for (int i = 0, v; i < e[u].size(); ++i) {v = e[u][i];if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (!leader[v])low[u] = min(low[u], dfn[v]);}if (dfn[u] == low[u]) {for (++cnt; sta.top() != u; sta.pop()) leader[sta.top()] = cnt;leader[sta.top()] = cnt;sta.pop();}
}signed main() {scanf("%d%d", &n, &m);for (int i = 1, a, x, b, y; i <= m; ++i) {scanf("%d%d%d%d", &a, &x, &b, &y);if (!x && !y)AddEdge(a + n, b), AddEdge(b + n, a);else if (x && y)AddEdge(a, b + n), AddEdge(b, a + n);else if (!x && y)AddEdge(b, a), AddEdge(a + n, b + n);else if (x && !y)AddEdge(a, b), AddEdge(b + n, a + n);  // a 表示 a0, a + n 表示 a1}for (int i = 1; i <= (n << 1); ++i)if (!dfn[i])Tarjan(i);for (int i = 1; i <= n; ++i)if (leader[i] == leader[i + n])  // 若 a0 和 a1 必须同时选, 就无解return puts("IMPOSSIBLE"), 0;puts("POSSIBLE");for (int i = 1; i <= n; ++i) printf("%d ", leader[i] > leader[i + n]);  // 输出一组解return 0;
}

应用

P3825 [NOI2017] 游戏

给定一串序列，有 \(d\) 个 \(x\) 位置有三种选择，其他位置有两种选择，求解一种合法方案。

\(n \leq 5 \times 10^4, d \leq 8\)

暴力枚举每个 \(x\) 地图不填 \(A\) 或不填 \(B\) 。因为不填 \(A\) 就可以填 \(B, C\) ，不填 \(B\) 就可以填 \(A, C\) ，这样就包含了 \(A, B, C\) 三种赛车。

时间复杂度降为 \(O((n+m) \times 2^d)\)​ 。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 7;struct Graph {vector<int> e[N];inline void clear(int n) {for (int i = 1; i <= n; ++i)e[i].clear();}inline void insert(const int u, const int v) {e[u].emplace_back(v);}
} G;struct Node {int x, y;char cx, cy;
} nd[N];int dfn[N], low[N], leader[N], sta[N];
char str[N];int n, d, m, dfstime, top, scc;template <class T = int>
inline T read() {char c = getchar();bool sign = (c == '-');while (c < '0' || c > '9')c = getchar(), sign |= (c == '-');T x = 0;while ('0' <= c && c <= '9')x = (x << 1) + (x << 3) + (c & 15), c = getchar();return sign ? (~x + 1) : x;
}inline char readc() {char c = getchar();while (c < 'A' || c > 'Z')c = getchar();return c;
}inline int trans(int x) {return x <= n ? x + n : x - n;
}inline int getid(int x, char op) {if (str[x] == 'a')return op == 'b' ? x : x + n;elsereturn op == 'a' ? x : x + n;
}inline void clear(int n) {G.clear(n);memset(dfn + 1, 0, sizeof(int) * n);memset(low + 1, 0, sizeof(int) * n);memset(leader + 1, 0, sizeof(int) * n);dfstime = scc = 0;
}void Tarjan(int u) {dfn[u] = low[u] = ++dfstime, sta[++top] = u;for (int v : G.e[u]) {if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (!leader[v])low[u] = min(low[u], dfn[v]);}if (dfn[u] == low[u]) {++scc;while (sta[top] != u)leader[sta[top--]] = scc;leader[sta[top--]] = scc;}
}inline bool solve() {clear(n * 2);for (int i = 1; i <= m; ++i) {if (str[nd[i].x] == nd[i].cx)continue;int x = getid(nd[i].x, nd[i].cx), y = getid(nd[i].y, nd[i].cy);if (str[nd[i].y] == nd[i].cy)G.insert(x, trans(x));elseG.insert(x, y), G.insert(trans(y), trans(x));}for (int i = 1; i <= n * 2; ++i)if (!dfn[i])Tarjan(i);for (int i = 1; i <= n; ++i)if (leader[i] == leader[i + n])return false;return true;
}bool dfs(int pos) {if (pos > n)return solve();else if (str[pos] != 'x')return dfs(pos + 1);for (int i = 0; i < 2; ++i) {str[pos] = 'a' + i;if (dfs(pos + 1))return true;}return str[pos] = 'x', false;
}signed main() {n = read(), d = read();scanf("%s", str + 1);m = read();for (int i = 1; i <= m; ++i) {nd[i].x = read(), nd[i].cx = tolower(readc());nd[i].y = read(), nd[i].cy = tolower(readc());}if (!dfs(1))return puts("-1"), 0;for (int i = 1; i <= n; ++i)if (str[i] == 'a')putchar(leader[i] < leader[i + n] ? 'B' : 'C');else if (str[i] == 'b')putchar(leader[i] < leader[i + n] ? 'A' : 'C');elseputchar(leader[i] < leader[i + n] ? 'A' : 'B');return 0;
}

割点

定义：对于一个无向图，若把一个点删除后这个图的极大连通分量增加了，则这个点就是图的一个割点。

特判根节点。对于非根节点，若存在一个儿子点 \(v\) 使得 \(low_v \geq dfn_u\) （即不能回到祖先），则该点为割点。

P3388 【模板】割点（割顶）

void Tarjan(int u, int f) {dfn[u] = low[u] = ++dfstime;int sonsum = 0;for (int v : G.e[u])if (!dfn[v]) {++sonsum, Tarjan(v, u);low[u] = min(low[u], low[v]);if (f && low[v] >= dfn[u])tag[u] = true;} else if (v != f)low[u] = min(low[u], dfn[v]);if (!f && sonsum >= 2)tag[u] = true;
}

桥（割边）

定义：对于一个无向图，若把一条边删除后这个图的极大连通分量增加了，则这条边就是图的一个桥。

代码和割点差不多，只要改一处： \(low_v > dfn_u\) ，而且不用特判根节点。

void Tarjan(int u, int f) {dfn[u] = low[u] = ++dfstime;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].v;if (!dfn[v]) {Tarjan(v, u);if (low[v] > dfn[u])G.e[i].tag = G.e[i ^ 1].tag = true;low[u] = min(low[u], low[v]);} else if (v != f)low[u] = min(low[u], dfn[v]);}
}

边双连通

  • 边双连通：无向图中对于两点 \(u, v\) ，若满足删去任意边两点均连通，则称 \(u, v\) 边双连通。
  • 边双连通分量：不存在割边的极大连通块。

求解

遍历时不走割边即可求得边双。

也可以用栈维护 dfs 到的所有点，每次找到割边 \((fa,son)\) 就不断弹栈直到弹出 \(son\) ，则弹出的所有点是一个边双。

P8436 【模板】边双连通分量

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 7, M = 2e6 + 7;struct Graph {struct Edge {int nxt, v;bool tag;} e[M << 1];int head[N];int tot = 1;inline void insert(int u, int v) {e[++tot] = (Edge) {head[u], v}, head[u] = tot;}
} G;vector<vector<int> > bscc;int dfn[N], low[N];
bool vis[N];int n, m, dfstime;void Tarjan(int u, int f) {dfn[u] = low[u] = ++dfstime;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].v;if (!dfn[v]) {Tarjan(v, u);if (low[v] > dfn[u])G.e[i].tag = G.e[i ^ 1].tag = true;low[u] = min(low[u], low[v]);} else if (v != f)low[u] = min(low[u], dfn[v]);}
}void dfs(int u) {bscc.back().emplace_back(u);vis[u] = true;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].v;if (!vis[v] && !G.e[i].tag)dfs(v);}
}signed main() {n = read(), m = read();for (int i = 1; i <= m; ++i) {int u = read(), v = read();if (u != v)G.insert(u, v), G.insert(v, u);}for (int i = 1; i <= n; ++i)if (!dfn[i])Tarjan(i, 0);for (int i = 1; i <= n; ++i)if (!vis[i])bscc.emplace_back(vector<int>()), dfs(i);printf("%d\n", bscc.size());for (auto it : bscc) {printf("%d ", it.size());for (int x : it)printf("%d ", x);puts("");}return 0;
}

相关结论

  • 边双对点有传递性。

  • 每个点恰属于一个边双。

  • 对于边双内任意一条 \(e\) ，存在经过 \(e\) 的回路。

  • 对于边双内任意两点 \(u, v\) ，存在经过 \(u, v\) 的回路。

  • 两点之间任意一条迹（不经过重复边的路径）上的所有割边，就是两点之间的所有必经边。

  • \(u, v\) 边双连通当且仅当 \(u, v\) 间无必经边。

点双连通

  • 点双连通：无向图中对于两点 \(u, v\) ，若满足删去任意除这两点以外的点两点均连通，则称 \(u, v\) 点双连通。
  • 点双连通分量：不存在割点的极大连通块。

求解

考虑建立一张新图，新图中的每个点对应原图中的每一条树边。

对于图中的每一条非树边，将其对应树上简单路径中的所有边在新图中对应的蓝点连成一个连通块。

这样，一个点不是割点当且仅当与其相连的所有边在新图中对应的蓝点都属于同一个连通块，两个点点双连通当且仅当它们在原图的树上路径中的所有边在新图中对应的蓝点都属于同一个连通块。

可以利用差分维护蓝点间的联通关系。

P8435 【模板】点双连通分量

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 7;struct Graph {vector<int> e[N];inline void insert(const int u, const int v) {e[u].emplace_back(v);}
} G;vector<vector<int> > Ans;int dfn[N], low[N], sta[N];int n, m, dfstime, top;template <class T = int>
inline T read() {char c = getchar();bool sign = (c == '-');while (c < '0' || c > '9')c = getchar(), sign |= (c == '-');T x = 0;while ('0' <= c && c <= '9')x = (x << 1) + (x << 3) + (c & 15), c = getchar();return sign ? (~x + 1) : x;
}void Tarjan(int u, int f) {dfn[u] = low[u] = ++dfstime, sta[++top] = u;int sonsum = 0;for (int v : G.e[u])if (!dfn[v]) {Tarjan(v, u), ++sonsum;low[u] = min(low[u], low[v]);if (low[v] >= dfn[u]) {Ans.emplace_back(vector<int>{u});while (sta[top] != v)Ans.back().emplace_back(sta[top--]);Ans.back().emplace_back(sta[top--]);}} else if (v != f)low[u] = min(low[u], dfn[v]);if (!f && !sonsum)Ans.emplace_back(vector<int>{u});
}signed main() {n = read(), m = read();for (int i = 1; i <= m; ++i) {int u = read(), v = read();G.insert(u, v), G.insert(v, u);}for (int i = 1; i <= n; ++i)if (!dfn[i])Tarjan(i, 0);printf("%d\n", Ans.size());for (auto it : Ans) {printf("%d ", it.size());for (int x : it)printf("%d ", x);puts("");}return 0;
}

相关结论

  • 点双对点不具有传递性。
  • 每条边恰属于一个点双。
  • 一个点是割点当且仅当它属于多个点双。
  • 由一条边直接相连的两个点点双连通。
  • 对于点双内的任意点 \(u\) ，存在经过 \(u\) 的简单环。
  • 对于边双内任意两点 \(u, v\) ，存在经过 \(u, v\) 的简单环。
  • 当 \(n \geq 3\) 时，在边中间插入点不影响点双连通性，因此钦定经过一个点和经过一条边是几乎等价的。
  • 对 \(n \geq 3\) 的点双中任意点 \(u\) 与任意边 \(e\) ，存在经过 \(u, e\) 的简单环。
  • 对 \(n \geq 3\) 的点双中任意不同两点 \(u, v\) 与任意边 \(e\) ，存在 \(u \ e \rightsquigarrow v\) 的简单路径。
  • 对 \(n \geq 3\) 的点双中任意不同三点 \(u, v, w\) ，存在 \(u \to v \to w\) 的简单路径。
  • 两点之间任意一条路径上的所有割点，就是两点之间的所有必经点。
  • 若两点双有交，那么交点一定是割点。

应用

P8456 「SWTR-8」地地铁铁

给定边权为 \(0\) 或 \(1\) 的无向连通图，求有多少组点对之间存在同时经过 \(0\) 和 \(1\) 的简单路径。

\(n \leq 4 \times 10^5, m \leq 10^6\)

对于落在不同点双的点对，如果经过的点双包含 \(0\) 边和 \(1\) 边则合法，否则显然不合法。

对于落在相同点双的点对，如果点双内部边权相同，显然不合法，否则只有一对特殊点（点双唯二既有 \(0\) 出边又有 \(1\) 出边的点对）不合法。

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 4e5 + 7, M = 1e6 + 7;struct DSU {int fa[N << 1], siz[N << 1];inline void prework(int n, int ext) {iota(fa + 1, fa + 1 + n + ext, 1);fill(siz + 1, siz + 1 + n, 1);fill(siz + 1 + n, siz + 1 + n + ext, 0);}inline int find(int x) {while (x != fa[x])fa[x] = fa[fa[x]], x = fa[x];return x;}inline void merge(int x, int y) {x = find(x), y = find(y);if (x == y)return;fa[y] = x, siz[x] += siz[y];}
} dsu1, dsu2;struct Graph {struct Edge {int nxt, v, w;} e[M << 1];int head[N];int tot = 1;inline void insert(int u, int v, int w) {e[++tot] = (Edge) {head[u], v, w}, head[u] = tot;}
} G;vector<int> bscc[N];int dfn[N], low[N], sta[N], esta[M], tag[N], tp[N];
bool in[M];ll ans;
int testid, n, m, dfstime, top, etop, ext;template <class T = int>
inline T read() {char c = getchar();bool sign = (c == '-');while (c < '0' || c > '9')c = getchar(), sign |= (c == '-');T x = 0;while ('0' <= c && c <= '9')x = (x << 1) + (x << 3) + (c & 15), c = getchar();return sign ? (~x + 1) : x;
}inline char readc() {char c = getchar();while (c != 'd' && c != 'D')c = getchar();return c;
}void Tarjan(int u) {dfn[u] = low[u] = ++dfstime, sta[++top] = u;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].v;if (!dfn[v]) {in[esta[++etop] = i >> 1] = true;Tarjan(v);low[u] = min(low[u], low[v]);if (low[v] >= dfn[u]) {bscc[++ext].emplace_back(u);while (sta[top] != v)bscc[ext].emplace_back(sta[top--]);bscc[ext].emplace_back(sta[top--]);vector<int> E;while (esta[etop] != (i >> 1))E.emplace_back(esta[etop--]);E.emplace_back(esta[etop--]);for (int x : E) {in[x] = false;tp[ext] |= 1 << G.e[x << 1].w;tag[G.e[x << 1].v] |= 1 << G.e[x << 1].w;tag[G.e[x << 1 | 1].v] |= 1 << G.e[x << 1].w;}int sum = 0;for (int x : bscc[ext])sum += (tag[x] == 3), tag[x] = 0;if (sum == 2)--ans;}} else {low[u] = min(low[u], dfn[v]);if (dfn[v] < dfn[u] && !in[i >> 1])esta[++etop] = i >> 1;}}
}signed main() {testid = read(), n = read(), m = read();for (int i = 1; i <= m; ++i) {int u = read(), v = read(), w = (readc() == 'd');G.insert(u, v, w), G.insert(v, u, w);}ans = 1ll * n * (n - 1) / 2;Tarjan(1);dsu1.prework(n, ext), dsu2.prework(n, ext);for (int u = 1; u <= ext; ++u)for (int v : bscc[u])if (tp[u] == 1)dsu1.merge(u + n, v);else if (tp[u] == 2)dsu2.merge(u + n, v);for (int i = 1; i <= n + ext; ++i) {if (dsu1.find(i) == i)ans -= 1ll * dsu1.siz[i] * (dsu1.siz[i] - 1) / 2;if (dsu2.find(i) == i)ans -= 1ll * dsu2.siz[i] * (dsu2.siz[i] - 1) / 2;}printf("%lld", ans);return 0;
}

连通度

  • 边连通度：对任意不同的两点 \(u, v\) ，使 \(u, v\) 不连通所需删去的边的数量的最小值 \(k\) 等于 \(u, v\) 之间边不相交的迹的数量的最大值，\(k\) 即为 \(u, v\) 间的边连通度。
  • 点连通度：对任意不同且不相邻的两点 \(u, v\) ，使得 \(u, v\) 不连通所需删去的点（除去 \(u, v\) ）的数量的最小值 \(k\) 等于 \(u, v\) 之间点（除去 \(u, v\) ）不相交的路径数量的最大值，\(k\) 即为 \(u, v\) 间的点连通度。

\(k\) -边连通当且仅当任意两点之间 \(k\) -边连通，点连通同理。

可以用最大流计算边连通度。

Menger 定理：两点间的迹的最大数量等于割集的最小大小。

Whitney 不等式：边连通度不大于点连通度不大于最小度，且对每个满足它的三元组，均可以找出满足这个三元组的图。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/745125.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

DC1主机渗透测试报告

DC1主机渗透测试报告

概述测试目的通过模拟黑客的渗透测试，评估目标系统是否存在可以被攻击者真实利用的漏洞以及由此引起的风险大小，为制定相应的安全措施与解决方案提供实际的依据。分析客户WEB应用系统的安全现状，检测WEB应用系统的漏洞和安全问题，并验证其他已知的脆弱点。对系统的任何弱点…
阅读更多...
ruoyi-flow 是一个轻量、灵活的工作流引擎， 真正的国产工作流引擎 （非BPM）。 其特点简洁轻量、独立组件、易扩展、易集成，且还拥有一个简洁美观的流程设计器。

ruoyi-flow 是一个轻量、灵活的工作流引擎， 真正的国产工作流引擎 （非BPM）。 其特点简洁轻量、独立组件、易扩展、易集成，且还拥有一个简洁美观的流程设计器。

ruoyi-flow 项目概述 项目介绍 ruoyi-flow 是一个轻量、灵活的工作流引擎， 真正的国产工作流引擎 （非BPM）。 其特点简洁轻量、独立组件、易扩展、易集成，且还拥有一个简洁美观的流程设计器。 项目背景 开源的流程引擎也好状态机引擎也好不可谓不多，他们的优点是功能很完备…
阅读更多...
C#写个简单的windows服务+部署

C#写个简单的windows服务+部署

部署： cd C:\Windows\Microsoft.NET\Framework\v4.0.30319 InstallUtil.exe C:\Users\Administrator\source\repos\WindowsService1\WindowsService1\bin\Debug\WindowsService1.exe 启动 停止 日志： 😘宝子：除非不再醒来，除非太阳不再升起，不然都请你好好生活，挣扎着…
阅读更多...
laravel11:发生异常时返回json

laravel11:发生异常时返回json

一，未配置前laravel11直接render页面 如图:二，配置 1, bootstrap/app.php <?phpuse Illuminate\Http\Request; use Illuminate\Auth\AuthenticationException; use Illuminate\Database\Eloquent\ModelNotFoundException; use Illuminate\Foundation\Application; use I…
阅读更多...
W外链创建小红书私信卡片教程

W外链创建小红书私信卡片教程

在当今的社交媒体时代，小红书以其独特的社区属性和用户粘性，成为了许多品牌和个人展示自己、推广产品的重要平台。而在小红书上，一张精美且富有吸引力的卡片往往能够迅速吸引用户的注意，提高点击率和转化率。本文将详细介绍如何使用W外链来创建小红书卡片，帮助你在小红书上…
阅读更多...
kettle从入门到精通 第七十六课 ETL之kettle kettle连接hive教程

kettle从入门到精通 第七十六课 ETL之kettle kettle连接hive教程

1、群里有小伙伴询问kettle连接hive的demo，今天抽点时间整理下。其实kettle连接hive和连接mysql数据库也是一样的。 1）kettle中的lib目录下放hive驱动jar，这里我使用的是kyuubi-hive-jdbc-shaded-1.9.0.jar。 2）设置hive连接参数。 3）通过表输入进行读取数据。 2、下载kyu…
阅读更多...
火山引擎ByteHouse发布高性能全文检索引擎

火山引擎ByteHouse发布高性能全文检索引擎

作为一款定位为OLAP的分析型数据库，ByteHouse在支持结构化数据检索方面具备先天优势，而此次发布的全文检索引擎则补齐了对非结构化、半结构化等数据的快速检索能力，让用户可以构建一体化的数据管理、查询服务，降低运维成本和资源成本。更多技术交流、求职机会，欢迎关注字节…
阅读更多...
Swift实现自定义Emoji、自定义表情、自定义键盘

Swift实现自定义Emoji、自定义表情、自定义键盘

实现自定义表情键盘效果如下demo 参考自PPStickerKeyboard
阅读更多...
外卖霸王餐系统，霸王餐API接口，美团/饿了么全国200+城市

外卖霸王餐系统，霸王餐API接口，美团/饿了么全国200+城市

微客云免费提供外卖霸王餐系统，支持分站、运营商、商家后台、独立域名，自定义品牌，自主收款。 随着科技的快速发展，数字化和网络化已经渗透到我们生活的方方面面。在餐饮行业中，API（应用程序编程接口）接口的广泛应用不仅提升了餐厅的运营效率，也为消费者带来了更加便捷…
阅读更多...
2024牛客暑期多校训练营1 I.Mirror Maze（题解）

2024牛客暑期多校训练营1 I.Mirror Maze（题解）

2024牛客暑期多校训练营1 I.Mirror Maze（题解），大模拟题意 给一个 \(n \times m\) 的二维char数组，由4种镜子组成，\, /, -, |，镜面反射规则就是根据光线的方向和镜面的角度符合直觉的反射，然后有多组询问 \(q \leq 10^6\)，每次给定起始位置和光线方向，求该光会经过多少…
阅读更多...
基于M3u8的视频加密及播放

基于M3u8的视频加密及播放

准备工作安装ffmpeg mac安装 brew install ffmpeg加密准备生成enc.keyopenssl rand 16 > enc.key （ 生成一个enc.key文件 ）生成 ivopenssl rand -hex 16 （ 生成一段字符串，记下来）新建一个文件 enc.keyinfo 内容格式如下：Key URI # enc.key的路径，使用http形式 Pa…
阅读更多...
zabbix6.4分离部署笔记

zabbix6.4分离部署笔记

Zabbix 6.4 分离部署实施过程 一、环境准备 三台服务器### 操作系统:RED HAT ENTERPRISE LINUX 8.3 数据库:MYSQL8.0 ip地址以及用途：Zabbix 前端，8C 16G 16G系统盘100G：10.0.13.71 1371zabbixwebZabbix服务后端,8C 16G 100G：10.0.13.63 1363zabbixserverZabbix数据库MySql…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023