笔记
2023年11月16日 35 0
【转载】浅谈 pb_ds 库及其在OI其他算竞中的应用
【原链接】
这篇太叼了!
pb_ds,比 STL 更强大的模板库。
upd. on 10.27 更新了优先队列的常数分析,增加了“万能头文件”的内容。
前言
之前看到过一篇关于 pb_ds 写得很好的文章,但现在找不到了;OI-wiki 上的内容的不太完整。那不如自己动手,丰衣足食。
当然,pb_ds 库中有很多东西 算竞 中是用不到的。为了方便,笔者会在基本不会用到的内容中减少笔墨。
也有许多东西笔者目前尚且不能理解,或者难以寻找到相关资料(主要是实现细节)。对于这些,笔者只能略过,请大神们谅解。
而对于一些可能不太准确的翻译,笔者将在后面补上其英文,以求准确。
本文约 14k 字,大约需要 30 分钟。
一、简介
pb_ds 库全程 policy_based data structure,即基于策略的数据结构。它包含关联容器和优先队列。
关联容器是元素是按照关键字来保存和访问的容器,与之相对的是顺序容器。pb_ds 中提供了 哈希表,平衡树,字典树,list_update(单向链表) 四种容器,结构如图所示:
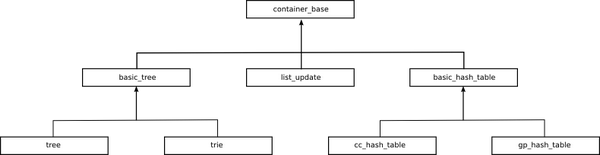
结构层次
而优先队列是指什么不言而喻,pb_ds 提供了 配对堆,二叉堆,二项堆,冗余计数二项堆和 thin_heap(类似斐波那契堆) 五种优先队列,可以说基本包含了所有堆结构。
pb_ds 使用的命名空间是 __gnu_pbds 而非 std(毕竟本来就不是标准库里面的)。
本文默认在 C++14 的选项下讨论。
二、关联容器零——assoc_container.hpp
assoc_container 是 关联容器(Associative Containers)的缩写。
该库文件中对 pb_ds 中的关联容器进行了声明,因此,使用关联容器时必须包含:
#include<ext/pb_ds/assoc_container.hpp>
语句。
当然你用 优先队列 是不需要这个的。
有一些博客认为该库文件是所有 pb_ds 容器的声明位置,这显然是不对的。应该注意。
打算竞当然无所谓(。
三、关联容器一——哈希表
1.简述
库文件是 hash_policy.hpp,使用哈希表时加上
#include<ext/pb_ds/hash_policy.hpp>
pb_ds 提供了两种哈希表,cc_hash_table 和 gp_hash_table,分别使用探测法和拉链法解决哈希冲突。
从理论上讲,探测法的复杂度是可以卡到 Θ(size)\Theta(size)Θ(size) 的,但实际很难。
拉链法的复杂度可以保持 Θ(1)\Theta(1)Θ(1) 级别。
2.原型
两者的原型是一样的,这里以 cc_hash_table 为例。
template<typename Key,typename Mapped,typename Hash_Fn = typename detail::default_hash_fn<Key>::type,typename Eq_Fn = typename detail::default_eq_fn<Key>::type,typename Comb_Probe_Fn = detail::default_comb_hash_fn::type,typename Probe_Fn = typename detail::default_probe_fn<Comb_Probe_Fn>::type,typename Resize_Policy = typename detail::default_resize_policy<Comb_Probe_Fn>::type,bool Store_Hash = detail::default_store_hash,typename _Alloc = std::allocator<char> >class cc_hash_table;
Key密钥类型。Mapped映射类型。Hash_Fn哈希函子(Hash functor)。根据文档的意思,似乎是将插入或查询的值变成一个非负积分的方法?Eq_Fn等价函子。Comb_Probe_Fn组合哈希函子(Combining hash functor),似乎是将之前转化的非负积分转化成一个位置?或者前面是null_hash_fn时候直接变成位置?Probe_Fn文档里没有/kk。Resize_Policy调整大小的原则。Store_Hash指示是否将哈希值与每个键一起存储。文档中说如果Hash_Fn是null_hash_fn且这一项为真则不会编译。_Alloc空间配置器类型。
当然算竞用到的只有前两个。
3.算竞中的构造方式
此处用 T、T1 等表示各种类型,下同。
__gnu_pbds::cc_hash_table<T1,T2>mp1;
__gnu_pbds::gp_hash_table<T1,T2>mp2;
4.使用(成员函数)
类似 unordered_map,这里说一些常用的。
运算符
= 赋值运算,表示一个新映射载入。
迭代器
begin 返回起始的迭代器。
end 返回最后一个元素后一个位置的迭代器。
注意没有 cend 和 cbegin。
容量
empty 返回是否为空。
size 返回大小。
max_size 返回理论可以放置的元素量。
修改器
clear 清空哈希表,返回 void()。
insert 插入一个映射,语法是 mp.insert({key,mapped}) 或 mp.insert(make_pair(key,mapped)),返回 pair<point_iterator, bool> 表示迭代器和插入是否成功。而且当 key 值已经存在一个映射时该语句是无效的,此时返回的 bool 为 0,即插入失败。
erase 擦除一个数,返回 void()。
没有 emplace 之类的。
查找
at 返回指定元素的引用并作越界检查。
operator[] 返回指定元素的引用。
find 返回迭代器,如未找到返回 end()。
时间复杂度均为 Θ(1)\Theta(1)Θ(1) 。
5.性能测试
原文档写的相当复杂,用处不大,故自己做了一些。
随机数据下,性能排名如下:std::map<__gnu_pbds::cc_hash_table<=std::unordered_map<__gnu_pbds::gp_hash_table。
而在构造好卡 umap 的数据下,排名如下:
std::unordered_map<<std::map<__gnu_pbds::cc_hash_table<__gnu_pbds::gp_hash_table。
之前说到,理论上讲,gp_hash_table 是可以卡到 Θ(size)\Theta(size)Θ(size) 的复杂度的,然而笔者并不知道如何卡,也没有在题目中见到。
随机数据下,cc_hash_table 要比 gp_hash_table 的常数大,时间一般是后者的 1.5~4 倍,空间更甚,最高可以到达 8 倍。
四、关联容器二——平衡树
1.简述
库文件是 tree_policy.hpp,库文件位置与 hash_policy.hpp 相同。
pb_ds 库提供了 basic_tree_tag、tree_tag、rb_tree_tag、splay_tree_tag、ov_tree_tag。前两个是后三个的基类,实际使用是没用的。而后三个分别是 红黑树,splay,有序向量树(本质就是一个排序向量,操作复杂度基本是 O(size)O(size)O(size) 的)。
2.原型
每个容器的原型都是一个,只是其中参数不同。
template<typename Key, typename Mapped, typename Cmp_Fn = std::less<Key>,typename Tag = rb_tree_tag,template<typename Node_CItr, typename Node_Itr,typename Cmp_Fn_, typename _Alloc_>
class Node_Update = null_node_update,typename _Alloc = std::allocator<char> >class tree
Key密钥类型,即想要存储的类型。Mapped映射类型。注意到有些地方写的是 映射规则(Mapped Policy),感觉更为准确。如果你想一般的使用平衡树,这里填__gnu_pbds::null_type即可。如果你想用成类似std::map的容器,这里填上你想映射成的类型。Cmp_Fn排序函子。默认是less<Key>即“小的”排在“前面”。Tag映射结构标记(Mapped-structure Tag),也就是你想用那种平衡树,这里选择填入简述中所说的几种。Node_Update节点更新类型(Node updater type),实现平衡树的细节。决定你可以在log或更小的复杂度内可以解决的问题。一般用tree_order_statistics_node_update以支持find_by_order和order_of_key。_Alloc空间适配器类型。
3.算竞中的构造
举一个比较常用的例子:
__gnu_pbds::tree<T,__gnu_pbds::null_type,less<T>,__gnu_pbds::rb_tree_tag,__gnu_pbds::tree_order_statistics_node_update>st;
如果你用不着 order_by_key 等,可以这样构造:
__gnu_pbds::tree<T,__gnu_pbds::null_type>st;
实现类似 std::map 的,只需要把上面两个中的 __gnu_pbds::null_type 改成你想映射成的类型即可。
4.使用(成员函数)
类似 std::set 但比它强大。
迭代器
begin 返回第一个迭代器,即最“小”元素的迭代器。
end 返回最后一个迭代器的后一个位置的迭代器。
类似地有 rbegin 和 rend,但是和 hash_table 一样没有 cbegin 和 cend。
容量
empty 返回是否为空。
size 返回容器大小。
max_size 返回理论最大值。
修改器
clear 清空容器,返回 void()。
insert 插入一个数,返回 pair<iterator,bool>,表示所在迭代器和插入是否成功。
erase 擦除一个数或迭代器,返回一个 bool 表示是否成功。
查找
find 找寻一个数,返回该数的迭代器,找不到则返回 end。
lower_bound 返回指向首个不小于给定键的元素的迭代器,找不到则返回 end。
upper_bound 返回指向首个不小于给定键的元素的迭代器,找不到则返回 end。
order_of_key(x) 返回 x 以比较的排名,排名定义为比 x “小”的数的数量。
find_by_order(x) 返回的排名 x 所对应元素的迭代器,排名定义为比一个数“小”的数的数量。
合并与分裂
join(x) 将 x 树并入当前树,前提是两棵树的类型一样,x 树被清空,返回 void()。前提是两棵树各自的最大值和最小值构成的区间不交,否则抛出 join_error 的逻辑错误(logic_error)并结束程序。而这前提在算竞中很难做到,故一般使用启发式合并来代替。
split(x,b)“小于等于” x 的属于当前树,其余的属于 b 树,返回 void()。
迭代器和容量部分时间复杂度为 O(1),其余除了 clear 为 O(size) 外全为 O(log size)。
5.性能测试
ov_tree_tag 由于复杂度就高,所以下文不讨论。
从官方文档来看,splay_tree_tag 在除了插入许多值然后反复查找一些值的表现中明显优于 rb_tree_tag 和 std::map 外,其他均比 rb_tree_tag 的所用时间长。
分裂与合并操作,由于 std::map 的高复杂度,速度很慢。除此之外均略逊于 rb_tree_tag。
从笔者的测评来看,在综合应用中,rb_tree_tag 可以明显优于 splay_tree_tag,但单独的插入或查询可能一般;有趣的是,顺序插入 [1,n] 时,rb_tree_tag 的时间大于后者,甚至在同时包含 tree_order.... 选项时前者有后者十倍的常数;而随机插入 n 个数时候,就恰恰相反,而在同时包含 tree_order.... 选项时后者有前者十倍的常数。
所以在算竞中建议使用 rb_tree_tag ,并且加入一次性大量数时可以的话 random_shuffle 一下。
另外,tree_order... 选项理论上会拖慢速度,实际确实如此。
五、关联容器三四——trie & list_update
1.简述
说实话感觉在算竞中相当鸡肋,两个都功能非常少且极为局限。但为了完整性,在此还是介绍一下。
trie 是 pb_ds 中的 字典树 接口,而 list_update 是 pb_ds 中的单向链表。
(不太理解为什么开发者认为单向链表是关联容器)。
库文件分别是 trie_policy.hpp 和 list_update_policy.hpp,也即:
#include<ext/pb_ds/trie_policy.hpp>
#include<ext/pb_ds/list_update_policy.hpp>
pb_ds 提供了两种 字典树,分别是 trie_tag 和 pat_trie_tag,即普通字典树和 PATRICIA trie,其中 PATRICIA 表示检索字母数字编码信息的实用算法(具体是那些笔者也不了解。。)。
2.原型
trie:
template<typename Key,typename Mapped,typename _ATraits = typename detail::default_trie_access_traits<Key>::type,typename Tag = pat_trie_tag,template<typename Node_CItr,typename Node_Itr,typename _ATraits_,typename _Alloc_>class Node_Update = null_node_update,typename _Alloc = std::allocator<char> >
class trie :
Key存储类型,即你想在字典树中插入什么(除string类型的亦可,但实现出来会比较异端)。Mapped映射类型,类似前文的tree容器,一般是null_type。_Atraits元素访问特征(Element-access traits),似乎用默认的即可,但是好像很多人用trie_string_access_traits<>,不太了解区别。Tag使用的类型,理论上两个都可以用,但实际上trie_tag好像不能?Node_Update节点更新类型,若想使用prefix_range需要trie_prefix_search_node_update。_Alloc空间适配器类型。
list_update:
template<typename Key,typename Mapped,class Eq_Fn = typename detail::default_eq_fn<Key>::type,class Update_Policy = detail::default_update_policy::type,class _Alloc = std::allocator<char> >class list_update
Key变量类型。Mapped映射类型。Eq_Fn等价函子,类似 哈希表中的。Update_policy更新方式。_Alloc空间适配器类型。
3.算竞中的构造
一般都是
__gnu_pbds::trie<string,__gnu_pbds::null_type,__gnu_pbds::trie_string_access_traits<>,__gnu_pbds::pat_trie_tag,__gnu_pbds::trie_prefix_search_node_update>tr;
__gnu_pbds::list_update<T,__gnu_pbds::null_type>li;
4.使用(成员函数)
trie:
insert 插入一个字符串,返回一个 pair<it,bool> 表示迭代器和是否插入成功。
erase 删除一个字符串,返回 bool 表示是否删除成功。
join(b) 将 b 树加入并清空 b 树。
find 寻找一个字符串,返回迭代器,找不到返回 end。
begin 返回第一个迭代器。
end 返回最后一个的下一个的迭代器。
--/++ 下一个或上一个迭代器。
prefix_range(x) 返回一个 pair 表示前缀为 x 的迭代器范围,使用时类似:
auto range=tr.prefix_range(x);
for(auto it=range.first;it!=range.second;it++);
来遍历前缀为 x 的所有字符串。
list_update:
begin 第一个迭代器。
end 最后一个迭代器的后一个。
insert 在前面加一个数。
甚至没有迭代器 ++/-- 的重载。
5.性能测试
官方文档认为,单独插入操作 pat_trie_tag 略逊于 std::map,而在查找中极大的优于 map 和平衡树。从理论上讲也确实如此。
但是 pat_trie_tag 或者说 trie 数有着很大的空间常数,这当然是事实,trie 树本就有 O(size) 的空间“常数“,在未知字典集时自然会更差。
六、优先队列
1.简述
库文件是 priority_queue.hpp,即需要包含:
#include<ext/pb_ds/priority_queue.hpp>
pb_ds 库提供了六种优先队列,即 priority_queue_tag、pairing_heap_tag、 binomial_heap_tag、rc_binomial_heap_tag、 binary_heap_tag 和 thin_heap_tag,分别是 基本堆结构(可以认为是后面的基类),配对堆,二项堆,冗余计数二项堆,二叉堆和一种类似于斐波那契堆的数据结构。
2.原型
template<typename _Tv,typename Cmp_Fn = std::less<_Tv>,typename Tag = pairing_heap_tag,typename _Alloc = std::allocator<char> >
class priority_queue
参数比较少(。
_Tv数据类型。Cmp_Fn比较函子(Comparison functor)例如less<_Tv>。Tag选择那种优先级队列。_Alloc空间适配器类型。
3.算竞中的构造
一般是
__gnu_pbds::priority_queue<T,greater<T>>dl;
4.使用(成员函数)
不同 tag 的成员函数基本相同,只是复杂度不一样,这个放在最后。
元素访问
top 返回堆顶元素。
容器大小
size 返回容器大小。
empty 返回容器是否为空。
修改器
push 插入一个元素,返回元素的迭代器。
pop 弹出堆顶,返回 void()。
modify(it,key) 将迭代器位置的元素改为 key,返回 void()。
erase(it) 删除迭代器位置的元素,返回 void()。
join(b): 把优先队列 b 合并进来并把 b 清空,返回 void()。
还是没有 emplace。
各个 tag 的时间复杂度:
用一个表格来描述
| | pop | push | modify | join | erase |
| — | — | — | — | — | — |
| 配对堆 | θ(1) | 最坏 θ(size)
均摊 θ(log size) | 最坏 θ(size)
均摊 θ(log size) | θ(1) | 最坏 θ(size)
均摊 θ(log size) |
| 二项堆 | 最坏 θ(log size)
均摊 θ(1) | O(log size) | O(log size) | O(log size) | O(log size) |
| 冗余计数二项堆 | θ(1) | O(log size) | O(log size) | O(log size) | O(log size) |
| 二叉堆 | 最坏 θ(size)
均摊 θ(log size)? | 最坏 θ(size)
均摊 θ(log size)? | θ(size) | θ(size) | O(size) |
| thin_heap_tag | θ(1) | 最坏 θ(size)
均摊 θ(log size) | 最坏 θ(size)
均摊 θ(log size) | θ(size) | 最坏 θ(size)
均摊 θ(log size) |
5.性能测试
官方文档认为,pairing_heap_tag 在非原生类型(如 std::string,官方文档也确实用的是这个)表现极佳,而在原生类型中不如 binary_heap_tag。
从笔者的测试来看,并没有感受到二叉堆在原生数据上的优势,甚至在单独的插入操作中还会被配对堆吊着打(应该是把复杂度卡上去的,所以吊着打应该主要不是常数问题,这里真的存疑)。
由于可并堆本身就是大常数数据结构,它的常数在容器大小不大略低于 std::pq,在很大时远不如 std::pq,故单独使用普通堆时建议使用 std::pq。
七、失效保证(invalidation_guarantee)
pb_ds 提供了三种失效保证,分别是:
basic_invalidation_guarantee – 基本失效保证,最弱的无效保证。可以保证在容器没有修改时候迭代器,指针等保持有效。
point_invalidation_guarantee – 点失效保证,更强的无效保证。可以保证在修改容器但迭代器等所指的东西没有被删除是保持有效。
range_invalidation_guarantee – 范围失效保证,最强的无效保证。在 点失效保证 的基础上,保证相对位置不变。
构造一个失效保证,可以用 __gnu_pbds::container_traits<T>::invalidation_guarantee 语句;检测其类型可以用 __cxa_demangle 函数。
检测结果如下:
哈希表中两个容器均为 点失效保证。
平衡树中 rb_tree_tag 和 splay_tree_tag 均范围失效保证,而 ov_tree_tag 为 基本失效保证。
优先队列中除了 binary_heap_tag 均为点失效保证。
八、例题
1.哈希表
被迫不自觉了(
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define pd __gnu_pbds
using namespace std;//难评的习惯
pd::cc_hash_table<string,bool>mp;
int n,num;
string s;
signed main(){
cin.tie(0)->sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;++i){
cin>>s;
if(mp.find(s)==mp.end())++num;//判定哈希表中有无某个密钥时的常用方法
//虽然这里可以但不建议写 if(!mp[s]),因为在一些记忆化搜索里这样写无法保证复杂度。
mp[s]=1;
}
cout<<num<<'\n';
return 0;
}
2.平衡树
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#define pd __gnu_pbds
using namespace std;
int n,m,a,op,x,last;
int ans=0;
template<typename pi>
using ptree=pd::tree<pi,pd::null_type,less<pi>,pd::rb_tree_tag,\pd::tree_order_statistics_node_update>;
ptree<pair<int,int> >st;
//pb_ds 中的平衡树类似 set,是会删除相同元素的,所以我们需要一个 pair 来区分不同先后的元素。
signed main(){
cin.tie(0)->sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;++i){
cin>>a;
st.insert(make_pair(a,-i));//用 i 来表示先后
}
for(int i=1;i<=m;++i){
cin>>op>>x;
x^=last;
if(op==1)st.insert(make_pair(x,i));
else if(op==2){
auto tp=*st.lower_bound(make_pair(x,-2*n));
//把 second 的值设的很小,如果有这个数保证可以找到
st.erase(tp);
}else if(op==3)last=st.order_of_key(make_pair(x,-2*n))+1;//注意平衡树容器中的顺序定义为严格小于它的数的个数
else if(op==4)last=(st.find_by_order(x-1)->first);
else if(op==5){
auto tp=*(--st.lower_bound(make_pair(x,-2*n)));
last=tp.first;
}else{
auto tp=*(st.upper_bound(make_pair(x,i+1)));
last=tp.first;
}
if(op>2)ans^=last;//不敢每次都异或啊(
}
cout<<ans<<'\n';
return 0;
}
3.字典树
实际不能通过本题,但还是放上吧:
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/trie_policy.hpp>
using namespace std;
#define pd __gnu_pbds
int T,n,q;
string s;
pd::trie<string,pd::null_type,pd::trie_string_access_traits<>,\
pd::pat_trie_tag,pd::trie_prefix_search_node_update>tr;
signed main(){
ios::sync_with_stdio(0);
cin>>T;
while(T--){
tr.clear();
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>s;
tr.insert(s);
}
while(q--){
cin>>s;
auto xr=tr.prefix_range(s);
//注意这里返回值是一个 pair<it,it>,所以下面不是 begin() 和 end()
int num=0;
for(auto x=xr.first;x!=xr.second;++x)++num;
//这里是 O(n)(θ(ans)) 的,所以不能通过本题。//这也就是为什么笔者说它功能很少,其实不能满足使用需求。
cout<<num<<'\n';
}
}
return 0;
}
4.list_update
没有例题,用以下程序来理解吧:
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/list_update_policy.hpp>
using namespace std;
__gnu_pbds::list_update<int,__gnu_pbds::null_type>ls;
signed main(){
ls.insert(1);
cout<<*ls.begin()<<' ';
ls.insert(2);
cout<<*ls.begin()<<'\n';
return 0;
}
输出 1 2。
5.优先队列
#include<bits/stdc++.h>
#include<ext/pb_ds/priority_queue.hpp>
using namespace std;
#define pd __gnu_pbds
int n,m;
int x,op,y;
int fa[100005];
bool death[100005];
pd::priority_queue<pair<int,int>,greater<pair<int,int> > >dl[100005];
//注意这里是 greater
int find(int x){return (x==fa[x]?x:fa[x]=find(fa[x]));}
signed main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;++i){
cin>>x;
dl[i].push(make_pair(x,i));
//使用 pair 来确定这是“第几个数”
//当然它是不会像 set 一样“吃元素”的。
}
for(int i=1;i<=n;++i)fa[i]=i;
for(int i=1;i<=m;++i){
cin>>op;
if(op==1){
cin>>x>>y;
if(death[x] or death[y])continue;
int fx=find(x),fy=find(y);
if(fx==fy)continue;
fa[fx]=fy;
dl[fy].join(dl[fx]);//合并并清空
}else{
cin>>x;
if(death[x]){cout<<-1<<'\n';continue;}
int fx=find(x);
auto x=dl[fx].top();dl[fx].pop();
death[x.second]=1;
cout<<x.first<<'\n';
}
}
return 0;
}
九、其他
1.pb_ds 的“万能头文件“
pb_ds 的头文件是不在万能头中的,而且头文件较多,可能不太方便。
可以使用
来包含 ext 库中所有的头文件(例如 pb_ds 和 rope)。
但是这句话在非 Ubuntu 环境下可能会显示缺失 iconv.h(该文件主要功能是 iconv 命令,可以将一种已知的字符集文件转换成另一种已知的字符集文件)。 当然你也可以在其他环境下自行配置。
这个在 OI 是可以使用的,因为 NOI-linux2.0 是 Ubuntu 环境;其他算竞不太了解。
Share Article:
C++, OI, 数据结构
![[BJDCTF2020]Mark loves cat(源码泄露+命令执行)](https://img2024.cnblogs.com/blog/3450162/202407/3450162-20240717121550392-1527648639.png)