一、曲线拟合简介
1、曲线拟合问题的提法
已知一组数据(二维),即平面上n个点 (xi,yi)(i=1,2,…,n), xi互不相同。寻求一个函数y=f(x),使得f(x)在某种准则下与所有的数据点最为接近,即拟合得最好。
2、线性最小二乘法
线性最小二乘法是解决曲线拟合最常用的方法,基本思路是,令
![]()
其中,r1(x),…,rm(x)是一组预先选定得一组线性无关的函数,a1,a2,…,am是待定系数.
涉及到的问题有二,一是系数确定;二是函数选取
2.1 系数确定
拟合准则:使得yi与f(xi)距离(称为残差)平方和最小,称为最小二乘法。,即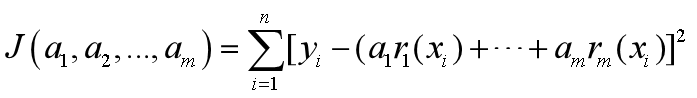
即求a1,…,am,转化为求J函数的最小值。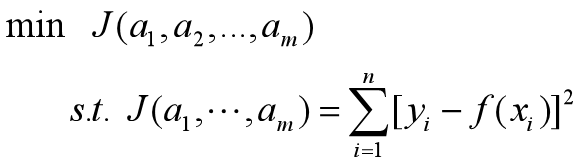
2.2 拟合函数的选取
拟合的前提是:
(1)通过机理分析,得到y和x的函数关系,这是r1(x),…, rm(x)也就好选取;
(2)若无法判断y和x的机理关系,绘制(xi,yi)的散点图,直观判断用什么曲线取拟合。
常用的曲线有
(1)线性![]()
(2)多项式![]() (一般m=2,3)
(一般m=2,3)
(3)双曲函数(一支)
(4)指数曲线![]()
一般需要几种曲线分别拟合,选最好的那个!
二、曲线拟合Matlab工具箱
1、多项式拟合
调用格式:a=polyfit(x0,y0,m)
x0,y0是数据向量,m表示多项式的阶数,返回的是多项式的降幂系数a=[a1,a2,…,am,am+1]。
要计算x处对应的多项式取值,需调用y=polyval(a,x)
例如:
x0=1990:1:1996;
x1=x0-1989;
y0=[70,122,144,152,174,196,202];
a=polyfit(x1,y0,3)
0.7778 -11.7381 71.6270 12.5714
![]()
2、最小二乘曲线拟合
调用格式:x=lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
其中, fun 为待拟合的函数,一般定义为F(x,xdata)的M文件; x0 参数初值值,一般用行向量给出; xdata,ydata 为观测值,列向量表示; lb 为参数的下界; ub 为参数的上届; options 为选项: