力扣-动态规划全解

目录

• 动态规划
  • 斐波那契数列-EASY
  • 爬楼梯-EASY
  • 使用最小花费爬楼梯-EASY
  • 不同路径-Middle
  • 不同路径II-Middle
  • 不同路径 III-HARD
  • 整数拆分-MID*
  • 不同的二叉搜索树-MID
• 背包问题-理论基础
  • 分割等和子集-EASY
  • 最后一块石头的重量 II-MID
  • 目标和-MID *
  • 一和零-MID*
  • 53-最大子数组和-中等
  • 918-环形子数组的最大和-中等
• 一维动态规划
  • 70-爬楼梯-简单
  • 198-打家劫舍-中等-记住
  • 139-单词拆分-中等
  • 322-零钱兑换-中等
  • 300-最长递增子序列-中等
• 多维动态规划
  • 120-三角形最小路径和
  • 64-最小路径和-中等
  • 63-不同路径Ⅱ-中等
  • 5-最长回文子串-中等
  • 97-交错字符串-中等
  • 72-编辑距离-中等
  • 123-买卖股票的最佳时机Ⅲ-困难
• 股票问题通用解法
  • 122-买卖股票的最佳时机Ⅱ-不限交易次数
  • 309-买卖股票的最佳时机 - 含冷冻期
  • 188-买卖股票的最佳时机Ⅳ - 至多交易k次
  • 恰好/至少交易k次，如何初始化
  • 121-买卖股票的最佳时机 - 只能交易一次 - 简单
  • 122-买卖股票的最佳时机Ⅱ-不限制交易次数-中等
  • 123-买卖股票的最佳时机Ⅲ-最多交易两次-困难
  • 188-买卖股票的最佳时机Ⅳ-最多交易k次-困难
  • 309-买卖股票的最佳时机-含冷冻期, 不限制交易次数-中等-再看看
  • 714-买卖股票的最佳时机-含手续费-中等

动态规划

• 基础类题目：斐波那契数列、爬楼梯
• 背包问题
• 打家劫舍，最后一道树形 DP
• 股票问题
• 子序列问题，编辑距离

注意：dp 数组的定义和下标的含义 & 递推公式 & dp 数组如何初始化 & 遍历顺序 & 打印 dp 数组

斐波那契数列-EASY

分析：

斐波那契数列 1 1 2 3 5 8

1. 确定 dp 数组的含义：dp[i], 下标 i, 第 i 个斐波那契数的值为 dp[i]
2. 确定递推公式：dp[i] = dp[i-1] + dp[i-2]
3. dp 数组如何初始化：dp[0] = 1, dp[1] = 1
4. 确定遍历顺序：从前向后遍历
5. 打印 dp 数组

代码

class Solution:def fib(self, n: int) -> int:if n <=1:return ndp = [0 for _ in range(n+1)]dp[0], dp[1] = 0, 1for i in range(2, n+1, 1):dp[i] = dp[i-1] + dp[i-2]return dp[n]

问题：n=45时答案错误

• 当n的值非常大时，使用列表来存储所有的斐波那契数可能会导致内存使用问题。
• 如果只需要最后一个斐波那契数（即dp[n]），则不需要存储整个序列。

优化代码

class Solution:def fib(self, n: int) -> int:if n <=1:return na, b = 0, 1for _ in range(2, n+1):a, b = b, a+breturn b

还是在 n=45 时出错

大整数溢出

可以使用取模运算来避免整数过大，如在计算斐波那契数时使用% 1000000007。

class Solution:def fib(self, n: int) -> int:if n <=1:return na, b = 0, 1for _ in range(2, n+1):a, b = b, (a+b) % 1000000007return b

时间复杂度logn的算法

爬楼梯-EASY

代码

class Solution:def climbStairs(self, n: int) -> int:# 定义 dp 数组dp = [0 for _ in range(n+1)]# dp[i] 表示 到达第 i 阶有多少种不同的方法dp[0] = 1dp[1] = 1for i in range(2, n+1):dp[i]  =dp[i-1] + dp[i-2]return dp[n]

思考

为什么爬楼梯不需要防止大整数溢出?

斐波那契数列的一个关键性质是它的项数随着指数增长，但是其值却以非常快的速率增长，很快就会超过大多数编程语言能够表示的整数范围。然而，对于爬楼梯问题，到达第 n 阶楼梯的方法数实际上总是一个正整数，并且这个数总是小于或等于 \(2^{n}\)。这是因为在最坏的情况下，每一步都只走 1 阶，这样就有 \(n\)种 方法；而每一步都走 2 阶，则最多有 \(\frac{n}{2} + \frac{n}{2}\)种方法，这在数值上不会超过 \(2^{n}\)。

使用最小花费爬楼梯-EASY

到达不花费，向上跳才花费。

代码

class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:min_cost = math.inf# 阶梯的层数 n = len(cost)# dp数组 dp[i]表示到达第i层的最低花费dp = [math.inf for _ in range(n+2)]# 顶楼为 n+1dp[0], dp[1] = 0, 0for i in range(2, n+1):dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])return dp[n]

不同路径-Middle

代码

class Solution:def uniquePaths(self, m: int, n: int) -> int:# 每次向下或向右一步# 定义二维 dp 数组# di[i][j]表示到达(i, j)的不同路径数dp = [[0 for _ in range(n)] for _ in range(m)]# 如果 i<m-1, 可以向下走# 如果 j<n-1，可以向右走# dp 数组初始化# 第一行，全为 1# 第一列，全为 1for j in range(n):dp[0][j] = 1for i in range(m):dp[i][0] = 1# 遍历for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i][j-1] + dp[i-1][j]return dp[m-1][n-1]

深搜代码 & 超时

class Solution:def uniquePaths(self, m: int, n: int) -> int:def dfs(i, j):if i > m or j > n:  # 越界了return 0if i == m and j == n:  # 找到一种方法return 1return dfs(i + 1, j) + dfs(i, j + 1)return dfs(1, 1)

不同路径II-Middle

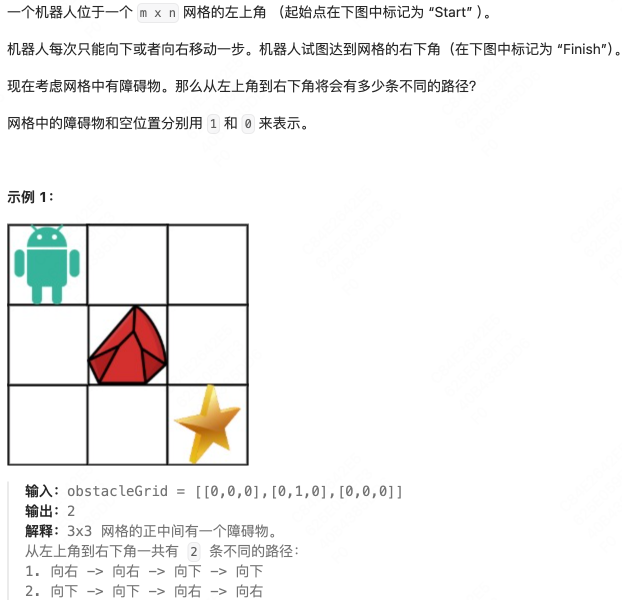
代码

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:# 每次向下或者向后，到右下角# 网格中有障碍物，障碍物网格# 定义 dp 数组，二维m, n = len(obstacleGrid), len(obstacleGrid[0])dp = [[0 for _ in range(n)] for _ in range(m)]# dp数组初始化# 障碍物处为 0# 第一行如果有障碍物，则右侧均为 0# 第一列如果有障碍物，则下方均为 0obs_flag = Falsefor j in range(n):if obstacleGrid[0][j] == 0 and not obs_flag:dp[0][j] = 1if obstacleGrid[0][j] == 1:obs_flag = Trueif obs_flag:dp[0][j] = 0obs_flag = Falsefor i in range(m):if obstacleGrid[i][0] == 0 and not obs_flag:dp[i][0] = 1if obstacleGrid[i][0] == 1:obs_flag = Trueif obs_flag:dp[i][0] = 0# 遍历# 如果当前位置上方有障碍，只能从左侧过来# 如果当前位置左侧有障碍，只能从右侧过来for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] != 1:dp[i][j] = dp[i-1][j] + dp[i][j-1]else:dp[i][j] = 0return dp[m-1][n-1]

不同路径 III-HARD

回溯代码 & 四个方向 & 路径数

class Solution:def uniquePathsIII(self, grid:List[List[int]]) -> int:m, n = len(grid), len(grid[0])def dfs(x:int, y:int, left:int) -> int:if x<0 or x>=m or y<0 or y>=n or grid[x][y]<0:return 0 # 不合法# 到达终点时必须要访问所有的无障碍方格if grid[x][y] == 2:return left == 0# 标记为已访问过grid[x][y] = -1# 对当前位置的上下左右四个方向进行递归搜索，并计算路径数。ans = dfs(x-1, y, left-1) + dfs(x, y-1, left-1) + dfs(x+1, y, left-1) + dfs(x, y+1, left-1)# 恢复现场grid[x][y] = 0return anscnt0 = sum(row.count(0) for row in grid)for i, row in enumerate(grid):for j, v in enumerate(row):if v == 1:return dfs(i, j, cnt0+1)

整数拆分-MID*

代码

class Solution:def integerBreak(self, n: int) -> int:# 拆分为 k 个正整数的和，且乘积最大化# 返回最大乘积# 定义 dp 数组，dp 数组的含义# dp[i] 将 i 拆分为 k 个正整数且乘积最大化dp = [0]*(n+1)dp[0] = 0dp[1] = 0dp[2] = 1for i in range(3, n+1):for j in range(1, int(i/2)+1):dp[i] = max(dp[i], j * dp[i-j], j*(i-j))print(dp)return dp[n]

思考

1. 对于所求 dp[i]，及要拆分的正整数 i
2. 将 i 拆分为 j 和 i-j，此时有两种方案
   1. i-j 不再拆分
   2. i-j 再次进行拆分，拆分之后的乘积依赖于dp[i-j]

不同的二叉搜索树-MID

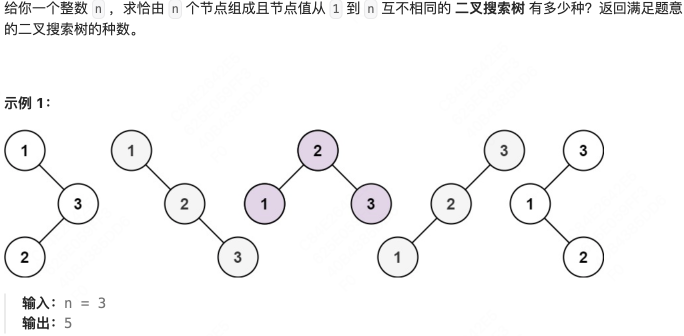
代码

class Solution:def numTrees(self, n: int) -> int:# 整数 n# n 个节点，1-n# 互不相同的二叉搜索树# 类似整数拆分# 11 个节点，左边 5 个，右边 5 个；左边 4 个，右边 6 个；# n = 0, 0# n = 1, 1 种# n = 2, 2 种dp = [0] * (n+1)dp[0] = 1dp[1] = 1if n <=1:return ndp[2] = 2for i in range(3, n+1):for j in range(0, i):# i个节点，i-1 在子树，拆分为j和i-1-jdp[i] += dp[j] * dp[i-1-j]return dp[n]

思考

1. 对 i 进行拆分，根节点占用一个值，实际拆分的是 i-1
2. 拆分为 j 和 i-1-j，左侧 j 个依赖于dp[j]，右侧 i-1-j 个，依赖于 dp[i-1-j]
3. 总的种数为左右两侧相乘
4. dp 数组输出化时，dp[0] = 1，0 个节点组成的二叉树不存在，但左侧子树 0 个节点时，算作一种，且需要与右侧种数相乘，故为 1

背包问题-理论基础

01 背包：n 种物品每种物品只有一个。

完全背包：n 种物品每种物品无限个。

多重背包：n 种物品每种物品个数各不相同。

01 背包问题

回溯算法暴力搜索

每个物品两种状态，取 & 不取。

二维 dp 数组解法

dp 数组的含义：[0, i]物品任取放入容量为 j 的背包

递推公式，对于 \(dp[i, j]\) 及物品 i：存在两种状态

1. 不放物品 i：依赖于\(dp[i-1, j]\)
2. 放物品 i：依赖于 \(dp[i-1, j-w[i]] + v[i]\)

dp数组初始化：行为物品，列为容量

• 第一行初始化，物品 0，如果容量大于物品 0 的容量，最大价值为物品 0 的价值，否则价值为 0.
• 第一列初始化，容量 0，如果物品小于容量 0，则价值为物品的价值，否则价值为 0.

遍历顺序：在这里二维 dp 数组先遍历物品再遍历背包或者先遍历背包再遍历物品都可以。

二维 dp 数组降至一维 dp 数组 & 滚动数组

每一行依赖于上一行的结果，将上一层数据拷贝下来。

dp 数组定义：dp[j] 表示容量为 j 的背包所能装下的最大价值为 dp[j]

递推公式：还是根据物品 i 来考虑的

1. 不放物品 i：就是 dp[j]
2. 放物品 i：\(dp[j-weight[i]] + value[i]\)

dp 数组的初始化：

• dp[0] = 0
• 非 0 下标时，也要初始化为 0，因为递推公式要对两个价值取最大值，这里应该初始化为一个小的值。

遍历顺序：先遍历物品，再遍历背包，且背包倒序遍历，防止物品重复放入。

面试题目

1. 01 背包问题，用二维dp数组实现，两个 for 循环能不能颠倒
2. 再用 1 维 dp 数组实现，两个 for 循环可不可以颠倒顺序，容量 for 循环为什么从后向前遍历，二维 dp 数组中为什么不用从后向前遍历
   1. 1 维 dp 数组是重复利用的

分割等和子集-EASY

一维 dp 数组 代码

class Solution:def canPartition(self, nums: List[int]) -> bool:# 等分为两部分if sum(nums) % 2 != 0:return Falsetarget = sum(nums) // 2# 定义一维 dp 数组# 含义：dp[i] 容量为 i 能够容纳的最大价值dp = [0] * (target+1)# 初始化，dp[0] = 0，非 0 时也为 0，后续有 max 操作# 主要这里对物品进行遍历for num in nums:# 对从0-target的所有容量进行遍历for j in range(target, num-1, -1):dp[j] = max(dp[j], dp[j-num] + num)return dp[target] == target

思路

• 抽象为 01 背包问题
• 背包容量是从 0 开始的

二维 dp 数组 代码

class Solution:def canPartition(self, nums: List[int]) -> bool:if sum(nums) % 2 != 0:return Falsetarget = sum(nums) // 2dp = [[False for _ in range(target + 1)] for _ in range(len(nums)+1)]# 初始化第一列for i in range(len(nums)+1):dp[i][0] = Truefor i in range(1, len(nums)+1):for j in range(1, target+1):if j < nums[i-1]:dp[i][j] = dp[i-1][j]else:dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i-1]]return dp[len(nums)][target]

最后一块石头的重量 II-MID

思考

1. 回溯暴力应该可以做
2. 背包问题
   1. 两两石头块进行粉碎，求最终的最小值，也可以转化为分成两堆，其和尽量接近，这样相减得到的值最小。

一维 dp 数组代码

class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:# 同样分成两堆，要求尽可能接近，这样碰撞的差值最小target = sum(stones) // 2# 定义一维 dp 数组dp = [0] * (target+1)# 含义 容量为 0 的背包，能装的最大价值# 初始化# 遍历顺序for i in range(len(stones)):# 内层循环保证了容量 j 都比 stone[i]要大for j in range(target, stones[i]-1, -1):dp[j] = max(dp[j], stones[i] + dp[j - stones[i]])return sum(stones) - dp[target]*2

目标和-MID *

思路

• 对于每一个元素，要么加要么减，类似于要么选，要么不选，所以回溯暴力算法应该可以解。
• 加和减也可以看做两个集合，（分割等和子集是两个集合相等，最后一块石头的重量是两个集合尽可能接近），这道题要求两个集合的总和为指定的 target。
• 给定的 nums 为非负整数数组，可以拆分为两个集合，两个集合相减最终得到的值为 target。

如果一个集合，被减数为 A

\(A - (sum-A) = target, A-sum + A = target\)

\(A = \frac{sum + target}{2}\)

故 \(sum + target\)一定能够整除 2.

dp 数组含义：dp[j] 表示容量为 j 的背包得到价值为 add 有 dp[j]种方法，总的方法为 dp[0] + dp[1] + … + dp[j]

问题就是在集合nums中找出和为 add 的组合。

确定递推公式

• 要求 dp[j]，如果加入 nums[i]，则取决于dp[j - nums[i]]
• 
• 类似的组合问题 dp[j] += dp[j - nums[i]]

一维 dp 数组代码

class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:# 题目拆解：运算结果等于 target == 背包容量为 target 时，容纳的最大价值为 target# 每个元素两种状态，加或减# 加集合，减集合# 要求加集合 - 减集合 = target# 问题抽象：加集合，背包问题，容量为加集合的背包所能容纳的物品价值恰好等于容量，且减去减集合后为 target# 加集合 = addif sum(nums) < abs(target):return 0add = (sum(nums) + target) // 2if (sum(nums) + target) % 2 != 0:return 0# 定义 dp 数组dp = [0] * (add + 1)# dp数组初始化# 背包容量为 0，装满背包有 1 中方法dp[0] = 1# 考虑物品 numfor num in nums:for j in range(add, num-1, -1):dp[j] += dp[j-num]return dp[add]

二维 dp 数组代码

class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:total_sum = sum(nums)if total_sum < abs(target):return 0if (target + total_sum) % 2 != 0:return 0# 目标和target_sum = (target + total_sum) // 2#创建二维 dp 数组，行表示选取的元素数量，列表示累加和dp = [[ 0 for _ in range(target_sum + 1)] for _ in range(len(nums)+1)]# 初始化：0 个物品装满容量为 0的背包，方法有一种dp[0][0] = 1# 遍历for i in range(1, len(nums)+1):# 容量从 0-target_sumfor j in range(target_sum+1):# 不选取当前物品dp[i][j] = dp[i-1][j]if j >= nums[i-1]:# 选当前物品dp[i][j] += dp[i-1][j - nums[i-1]]return dp[len(nums)][target_sum]

• 当前元素为 \(nums[i]\)，上一个元素为 \(nums[i-1]\)
  • 不选取当前物品时 ✅
  • 选取当前物品：如果当前容量为 j，要考虑当前容量是否大于上一个元素 \(nums[i-1]\)，如果大于则 \(dp[i][j]\) 可以依赖于 \(dp[i-1][j-nums[j-1]]\)
  • +=

一和零-MID*

子集需要满足：最多 m 个 0 ，最多 n 个 1

求：这样的子集最多有多少个元素

思路

m个 0，n 个 1 的容器，装满这个容器，最多有多少个元素。

容器==背包，两个维度的背包，之前的背包只有一个容量的维度，现在相当于是一个容量装 0，一个容量装 1，两个维度。

装满这个背包最多有多少个物品。

零一背包，每个物品只能使用一次。

3 个变量，m，n，最多多少个物品。

每个物品的重量其实就是每个字符串包含 x 个 0 和 y 个 1.

定义二维 dp 数组

\(dp[i][j]\) 定义为 m=i，n=j 的背包最多装多少个物品。

递推公式

当前物品的重量：x 个 0，y 个 1

选中当前物品之后，数量要+1

\(当前物品 重量(Num_0, Num_1) = (x, y)\)

\(dp[i-x][j-j] + 1\)

二维 dp 数组代码

class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:# 二进制字符串数组# 最大子集长度# 最大子集最多包含 m 个 0，n 个 1# 该子集看做一个背包，两个维度的背包 m 和 n# 定义二维 dp 数组dp = [[0 for _ in range(n+1)] for _ in range(m+1)]# 含义 dp[i][j]# m = i,n = j 的背包，最多装的物品数为 dp[i][j]# 初始化dp[0][0] = 0# 物品个数num  = len(strs)# 0维度重量weight_0 = [0] * numweight_1 = [0] * numfor idx, ss in enumerate(strs):for ch in ss:if ch=='1':weight_1[idx] += 1else:weight_0[idx] += 1# print(weight_0)# print(weight_1)# 初始化# 非 0 索引肯定初始化为 0 没问题，要取 max 操作# 第一行 & 第一列 是否需要额外处理# 遍历顺序# 遍历物品for idx in range(num):# 遍历背包 背包是二维的# 容量和物品重量的关系在 range 中进行限制for i in range(m, weight_0[idx]-1, -1):for j in range(n, weight_1[idx]-1, -1):dp[i][j] = max(dp[i][j], dp[i-weight_0[idx]][j-weight_1[idx]]+1)return dp[m][n]

53-最大子数组和-中等

动态规划

class Solution:def maxSubArray(self, nums: List[int]) -> int:'''最大和，连续子数组动态规划'''arr = nums.copy()for i in range(1, len(arr)):arr[i] = max(arr[i], arr[i-1]+arr[i])return max(arr)

918-环形子数组的最大和-中等

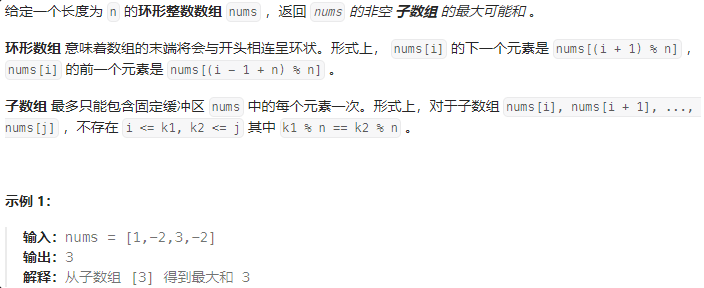
class Solution:def maxSubarraySumCircular(self, nums: List[int]) -> int:'''环形数组最大子数组的两种情况：1. 包含首尾：中间即为最小子数组，求最小子数组和2. 不包含首尾维护最大前缀和 & 最小前缀和'''n = len(nums)max_ = float('-inf')min_ = float('inf')# 无环pre = 0     # 以nums[i]结尾的最大前缀和for i in range(n):if pre > 0:pre = pre + nums[i]else:pre = nums[i]max_ = max(max_, pre)# 如果最大子数组和小于0，说明数组全是负数，返回最大的负数即可if max_<0:return max(nums)# 有环pre = 0     # 以nums[i]结尾的最小前缀和for i in range(n):if pre > 0:pre = nums[i]else:pre = pre + nums[i]min_ = min(min_, pre)return max(max_, sum(nums)-min_)

一维动态规划

70-爬楼梯-简单

看示例，我们当前应该是处于第0阶

class Solution:def climbStairs(self, n: int) -> int:dp = [1] * (n+1)for i in range(2, n+1):dp[i] = dp[i-1]+ dp[i-2]return dp[n]

198-打家劫舍-中等-记住

class Solution:def rob(self, nums: List[int]) -> int:'''相邻的不能偷'''n = len(nums)dp = [0] * (n+1)# dp[i]表示偷窃前i个房子满足条件获得的最大值# dp[i]考虑当前nums[i-1]偷还是不偷dp[0] = 0dp[1] = nums[0]for i in range(2, n+1):dp[i] = max(dp[i-1], dp[i-2]+nums[i-1])return dp[n]

空间优化

class Solution:def rob(self, nums: List[int]) -> int:'''很多时候我们并不需要始终持有全部的 DP 数组对于小偷问题，我们发现，最后一步计算 f(n) 的时候，实际上只用到了 f(n−1) 和 f(n−2) 的结果只用两个变量保存两个子问题的结果，就可以依次计算出所有的子问题'''prev = 0curr = 0for i in nums:# 循环开始时，curr表示dp[i-1]，prev表示dp[i-2]prev, curr = curr, max(curr, prev+i)# 循环结束时，curr表示dp[i]，prev表示dp[i-1]return curr 

139-单词拆分-中等

动态规划

class Solution:def wordBreak(self, s: str, wordDict: List[str]) -> bool:'''回溯算法超时动态规划，表示字符串s的前i个字母是否能够被表示'''n = len(s)dp = [False] * (n+1)dp[0] = Truefor i in range(n): # 起点for j in range(i+1, n+1):if dp[i] and s[i:j] in wordDict:dp[j] = Truereturn dp[-1]

记忆化回溯

对剩余字符串进行递归调用，将剩余字符串的调用结果进行缓存

class Solution:def wordBreak(self, s: str, wordDict: List[str]) -> bool:'''记忆化回溯使用装饰器，装饰器可以保存函数的执行结果，缓存'''import functools# 使用lru_cache装饰器来缓存back_track函数的结果，None参数表示缓存所有调用的结果，有助于避免重复计算@functools.lru_cache(None)def back_track(s: str):# s为剩余需要匹配的字符串if not s:return Trueres = Falsefor i in range(1, len(s)+1):if s[:i] in wordDict:res = back_track(s[i:]) or resreturn resreturn back_track(s)

322-零钱兑换-中等

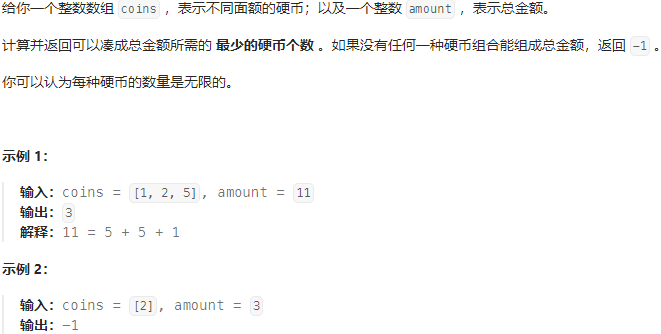
动态规划

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:''' 不同面额的硬币总金额凑成总金额所需的最少金币数'''dp = [math.inf] * (amount+1)dp[0] = 0for i in coins:if i<=amount:dp[i] = 1for i in range(1, amount+1):if dp[i] != math.inf:continuefor j in coins:if i-j >=1:dp[i] = min(dp[i], dp[i-j]+1)else:continueif dp[-1] == math.inf:return -1return dp[-1]

完全背包问题

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:n = amountdp = [math.inf] * (n+1)dp[0] = 0# 遍历物品for coin in coins:# 遍历背包for i in range(coin, n+1):dp[i] = min(dp[i], dp[i-coin]+1)if dp[-1] == math.inf:return -1return dp[-1]

300-最长递增子序列-中等

动态规划

class Solution:def lengthOfLIS(self, nums: List[int]) -> int:'''最长增长子序列整数数组，严格递增 子序列 相对顺序不改变'''n = len(nums)dp = [1] * n # dp[i] 表示到i为止最长的递增子序列for i in range(n):for j in range(i, -1, -1):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j]+1)return max(dp)

多维动态规划

120-三角形最小路径和

动态规划，填充主对角线左侧三角区域

class Solution:def minimumTotal(self, triangle: List[List[int]]) -> int:'''只能移动到下一行的相邻结点二维dp数组'''n = len(triangle)dp = [[math.inf for _ in range(n)] for _ in range(n)]dp[0][0] = triangle[0][0]# 从第二行开始处理for i in range(1, n):for j in range(i+1):# 当前坐标 (i, j)if j-1>=0:dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]else:dp[i][j] = dp[i-1][j] + triangle[i][j]return min(dp[-1])

64-最小路径和-中等

class Solution:def minPathSum(self, grid: List[List[int]]) -> int:'''每次只能向右或向下'''m = len(grid)n = len(grid[0])dp = [[math.inf for _ in range(n)]for _ in range(m)]# 初始化第一行for i in range(n):dp[0][i] = grid[0][i]if i>0:dp[0][i] += dp[0][i-1]# 初始化第一列for i in range(m):dp[i][0] = grid[i][0]if i>0:dp[i][0] += dp[i-1][0]# 遍历for i in range(1, m):for j in range(1, n):dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]return dp[-1][-1]

63-不同路径Ⅱ-中等

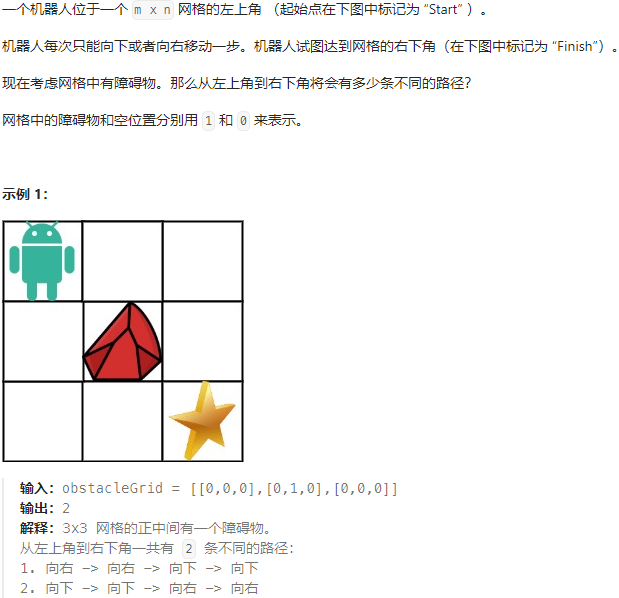
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:'''向下或向右二维dp数组记录到大当前位置有几种路径'''# 如果起始位置有石头，直接返回0if obstacleGrid[0][0] == 1:return 0m  = len(obstacleGrid)n = len(obstacleGrid[0])dp = [[0 for _ in range(n)]for _ in range(m)]dp[0][0] = 1# 初始化第一行i = 1while i<n:if obstacleGrid[0][i] == 1:breakdp[0][i] = 1i += 1while i<n:dp[0][i] = 0i += 1# 初始化第一列i = 1while i<m:if obstacleGrid[i][0] == 1:breakdp[i][0] = 1i += 1while i<m:dp[i][0] = 0i += 1# 遍历for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:dp[i][j] = 0elif dp[i-1][j] != 0 and dp[i][j-1] != 0:dp[i][j] = dp[i-1][j] + dp[i][j-1]else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[-1][-1]

5-最长回文子串-中等

❌错误的中心扩散法

这样选定中心点，同时向两边扩散，只能处理回文子串为奇数的情况，无法处理偶数的情况，如上述bb

class Solution:def longestPalindrome(self, s: str) -> str:'''中心扩散法'''max_len = 1res = s[0]n  =len(s)for i in range(n):left = i-1right = i+1while left >=0 and right <= n-1:if s[left] != s[right]:breakif right-left+1>max_len:max_len = right-left+1res = s[left:right+1]left -= 1right += 1return res

✔ 正确的中心扩散法

考虑当前中心点时，应将左右指针分别移动到不等于中心点处，再向左右扩展

class Solution:def longestPalindrome(self, s: str) -> str:if not s:return ''n = len(s)cur_len = 1  # ! 初始化为1max_len = 1res = s[0]for i in range(n):left = i-1right = i+1# 向左扩展回文子串while left>=0 and s[left] == s[i]:cur_len += 1left -= 1# 向右扩展回文子串while right<=n-1 and s[right] == s[i]:cur_len += 1right += 1# 上面的代码解决当中心点左右两侧与中心点字符相同的情况# 将left和right移动到与中心点不同的位置# 左右向两侧扩展while left >=0 and right <=n-1 and s[left]==s[right]:cur_len += 2left -= 1right += 1if cur_len > max_len:max_len = cur_lenres = s[left+1: right]cur_len = 1return res

动态规划

class Solution:def longestPalindrome(self, s: str) -> str:'''dp[l][r] 表示字符从l到r是否为回文串如果要判断dp[l-1][r+1]是否为回文串，必须dp[l][r]是回文，且s[l-1]==s[r+1]'''max_len = 0n = len(s)if n<2:return s res = s[0]dp = [[False for _ in range(n)]for _ in range(n)]# 初始化，对角线处为Truefor i in range(n):dp[i][i] = True # 遍历# 先枚举子串的长度for L in range(2, n+1):# 左边界for l in range(n):# 右边界r = l+L-1if r>n-1:breakif s[l] != s[r]:dp[l][r] = Falseelse:if r-l<3: # 🐖注意这里的处理!dp[l][r] = Trueelse:dp[l][r] = dp[l+1][r-1]if dp[l][r] and r-l+1 > max_len:max_len = r-l+1res = s[l:r+1]return res

97-交错字符串-中等

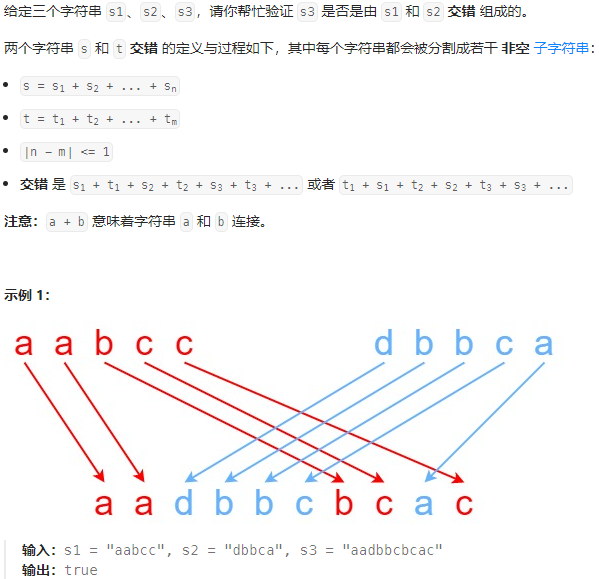
class Solution:def isInterleave(self, s1: str, s2: str, s3: str) -> bool:'''d[i][j] 表示s1的前i个和s2的前j个字符能够构成s3的前i+j个'''m = len(s1)n = len(s2)if m+n != len(s3):return Falsedp = [[ False for _ in range(n+1)]for _ in range(m+1)]# 初始化dp[0][0] = True# 初始化第一行，s2的前i个能否构成s3的前i个for i in range(1, n+1):if s2[:i] == s3[:i]:dp[0][i] = True# 初始化第一列，s1的前i个能否构成s3的前i个for i in range(1, m+1):if s1[:i] == s3[:i]:dp[i][0] = True# 遍历for i in range(1, m+1):for j in range(1, n+1):# dp[i][j]# s1的前i个字符与s2的前j-1个字符可以构成s3的前i+j-1个字符# 当前s2的第j个字符也等于s3的第i+j个字符# 则s1的前i个字符与s2的前j个字符可以构成s3的前i+j个字符if dp[i][j-1] and s2[j-1] == s3[i+j-1]:dp[i][j] = Trueif dp[i-1][j] and s1[i-1] == s3[i+j-1]:dp[i][j] = Truereturn dp[-1][-1]

72-编辑距离-中等

二维DP-错误代码❌

只考虑了修改和插入两个操作

class Solution:def minDistance(self, word1: str, word2: str) -> int:'''编辑距离，word1转换为word2所需的最小操作数二维dpdp[i][j] 表示 word1的前i个字符转换为word2的前j个字符需要的最小操作数三种操作：插入，删除，替换'''m = len(word1)n = len(word2)dp = [[math.inf for _ in range(n+1)] for _ in range(m+1)]# 初始化dp[0][0] = 0# 第一行，word1为空，转换为word2需要的最小次数for i in range(1, n+1):dp[0][i] = i# 第一列for i in range(1, m+1):dp[i][0] = i # 遍历for i in range(1, m+1):for j in range(1, n+1):# dp[i][j]if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:if j>i:dp[i][j] = dp[i][j-1]+1elif j<i:dp[i][j] = dp[i-1][j]+1else:dp[i][j] = dp[i-1][j-1]+1return dp[-1][-1]

二维DP-正确代码

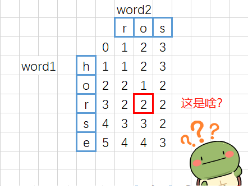
class Solution:def minDistance(self, word1: str, word2: str) -> int:'''编辑距离，word1转换为word2所需的最小操作数dp[i][j] 表示 word1的前i个字符转换为word2的前j个字符需要的最小操作数三种操作：插入，删除，替换如果word1和word2其中一个为空时，即全增加或全删除的情况插入：dp[i][j] = dp[i][j-1]+1删除：dp[i][j] = dp[i - 1][j] + 1修改：dp[i][j] = dp[i - 1][j - 1] + 1'''m = len(word1)n = len(word2)dp = [[math.inf for _ in range(n+1)] for _ in range(m+1)]# 初始化dp[0][0] = 0# 第一行，word1为空，转换为word2需要的最小次数for i in range(1, n+1):dp[0][i] = i# 第一列for i in range(1, m+1):dp[i][0] = i # 遍历for i in range(1, m+1):for j in range(1, n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:# 取增删改的最小值  修改         删除         插入dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1return dp[-1][-1]

123-买卖股票的最佳时机Ⅲ-困难

暴力-超时代码

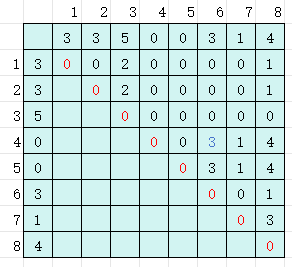
假设第i天买入，找到所有收益为正向的天数

从收益为正的天再次出发买入，找之后天卖出的最大收益

class Solution:def maxProfit(self, prices: List[int]) -> int:'''买卖股票的最佳时机获取最大利润最多买卖两次二维DP，第i天买，第j天卖'''n = len(prices)dp = [[0 for _ in range(n)] for _ in range(n)]# 主对角线均为0，代表当天买当天卖为0for i in range(n):for j in range(i+1, n):# 第i天买第j天卖dp[i][j] = prices[j]-prices[i] if prices[j]-prices[i]>0 else 0# 需要从中找两个买卖的端点max_prof = 0for i in range(n):# 找利润大于0的索引idx_list = []for idx, val in enumerate(dp[i]):if val == 0:continueidx_list.append(idx)for j in idx_list:cur_prof = 0# 第i天卖，第j天卖，第一次交易cur_prof += dp[i][j]# 第二次交易，在第j天之后寻找sec_prof = 0for k in range(j, n):sec_prof = max(sec_prof, max(dp[k]))cur_prof += sec_profif cur_prof > max_prof:max_prof = cur_profreturn max_prof

动态规划-正确代码

class Solution:def maxProfit(self, prices: List[int]) -> int:'''最多两笔买卖任意一天结束后，会处于以下状态之一：1. 未进行任何操作2. 只进行过一次买3. 一次买，一次卖，完成一次交易4. 一次交易完成，再次买入5. 完成两次交易第一种状态利润为0剩下的四种状态，分别将最大利润记为 buy1, sell1, buy2, sell2如果知道了第i-1天结束后的这四种状态，如何通过状态转移方程得到第i天结束后的四种状态1. 对于buy1，第i天结束可以不进行任何操作保持不变，也可以以价格prices[i]买入buy1 = max(buy1, -prices[i])2. 对于sell1，第 i 天我们可以不进行任何操作，保持不变，也可以在只进行过一次买操作的前提下以 prices[i] 的价格卖出股票sell1 = max(sell1, buy1+prices[i])3. 对于buy2，buy2 = max(buy2, sell1-prices[i])4. sell2 = max(sell2', buy2+prices[i])边界条件：第 i=0 天时的四个状态：以 prices[0] 的价格买入股票 buy1=-prices[0]sell1即为在同一天买入并且卖出，因此 sell1=0buy2 同一天买入卖出再以prices[0]买入 buy2=-prices[0]sell2 买入再卖出 sell2=0将这四个状态作为边界条件，从 i=1 开始进行动态规划，即可得到答案。在动态规划结束后，由于我们可以进行不超过两笔交易，因此最终的答案在0, sell1, sell2中的最大值在最有情况下，恰好进行一笔交易，也可以归为同一天卖出再买入的情况，最后返回sell2'''n = len(prices)# 第i=0天时买入buy1 = -prices[0] sell1 = 0buy2 = -prices[0]sell2 = 0# 理解这四个转移方程for i in range(1, n):buy1 = max(buy1, -prices[i])sell1 = max(sell1, buy1+prices[i])buy2 = max(buy2, sell1-prices[i])sell2 = max(sell2, buy2+prices[i])return sell2

股票问题通用解法

122-买卖股票的最佳时机Ⅱ-不限交易次数

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

为了后面改为递归，从最后一天向前思考。

启发思路：最后一天发生了什么？

从第0天开始到第5天结束时的利润 = 从第0天开始到第4天结束时的利润 + 第5天的利润

1.）如果第5天什么也不做，利润为0

2.）如果第5天买入股票，利润就是-4

3.）如果第5天卖出股票，利润就是+4

在第i-1天结束时，如果买入股票，那在第i天开始时的状态就是持有股票

在第i-1天结束时，如果卖出股票，那在第i天开始时的状态就是未持有股票

如果什么也不做，那么状态不变

这种表示状态之间转换关系的图叫状态机

从这张图中可以看出，状态转移有这4中情况

定义 dfs(i, 0) 表示到第i天结束时，未持有股票的最大利润

定义 dfs(i, 1) 表示到第i天结束时，持有股票的最大利润

由于第i-1天的结束就是第i天的开始

dfs(i-1, •)也表示到第i天开始时的最大利润

\(\begin{array}{l} d f s(i, 0)=\max (d f s(i-1,0), d f s(i-1,1)+\operatorname{prices}[i]) \\ d f s(i, 1)=\max (d f s(i-1,1), d f s(i-1,0)-\operatorname{prices}[i]) \end{array}\)

第i天结束时未持有股票的利润 = max( 第i-1天结束时未持有股票的利润，第i-1天结束时持有股票的利润 + 当前卖出的获得的利润 )

第i天结束时持有股票的利润 = max( 第i-1天结束时持有股票的利润， 第i-1天结束时未持有股票的利润 - 当前买入获得的利润)

递归边界，

dfs(-1, 0) = 0 第0天开始未持有股票，利润为0

dfs(-1, 1) = -∞ 第0天开始时不可能持有股票

递归入口

max( dfs(n-1, 0), dfs(n-1,1))

如果在最后一天还持有股票就卖不出去了，所以 dfs(n-1, 1)是不会比dfs(n-1, 0)大的。

所以递归入口是 dfs(n-1, 0)

不使用cache装饰器会超时，改为记忆化搜索

class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)# 需要改为记忆化搜索, cache装饰器@cachedef dfs(i, hold):if i<0:return -inf if hold else 0if hold:# 第i天结束时持有return max(dfs(i-1, True), dfs(i-1, False)-prices[i])# 第i天结束时未持有return max(dfs(i-1, False), dfs(i-1, True)+prices[i])return dfs(n-1, 0)

如果将递归翻译未递推的形式

插入一个状态表示i=-1

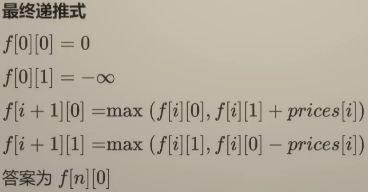
# 击败5%
class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)f = [[0]*2 for _ in range(n+1)]f[0][0] = 0f[0][1] = -inffor i, p in enumerate(prices):f[i+1][0] = max(f[i][0], f[i][1] + p)f[i+1][1] = max(f[i][1], f[i][0] - p)return f[-1][0]

空间优化

# 击败95%
class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)f0 = 0f1 = -inffor p in prices:new_f0 = max(f0, f1+p)f1 = max(f1, f0-p)f0 = new_f0return f0

309-买卖股票的最佳时机 - 含冷冻期

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

思考，除了是否持有股票的状态，现在新增了冷冻期的状态

买入股票的时候，前一天不能有卖出的操作，那么从再前一天转移过来

class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)@cachedef dfs(i, hold):if i<0:return -inf if hold else 0if hold:# 第i天结束时持有股票# 第i-1天结束时就持有，当前什么也不做# 第i-1天结束时未持有，当前买入# 买入之前不能有卖出return max(dfs(i-1, True), dfs(i-2, False)-prices[i])# 第i天结束时，未持有return max(dfs(i-1, False), dfs(i-1, True)+prices[i])return dfs(n-1, False)

188-买卖股票的最佳时机Ⅳ - 至多交易k次

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

有次数限制，应当在递归的过程中记录次数

定义 dfs(i, j, 0)表示第i天结束时完成至多j笔交易，未持有股票的最大利润

定义 dfs(i, j, 1)表示第i天结束时完成至多j笔交易，持有股票的最大利润

\(\begin{array}{l} \operatorname{dfs}(i, j, 0)=\max (d f s(i-1, j, 0), \operatorname{dfs}(i-1, j, 1)+\operatorname{prices}[i]) \\ \operatorname{dfs}(i, j, 1)=\max (d f s(i-1, j, 1), \operatorname{dfs}(i-1, j-1,0)-\operatorname{prices}[i]) \end{array}\)

第i天结束时最多完成j笔交易未持有，前一天结束时最多完成j笔交易未持有 什么也不做， 前一天结束时最多完成j笔交易持有 当前卖出

第i天结束时最多完成j笔交易持有，前一天结束时最多完成j笔交易持有 什么也不做，前一天结束时最多完成j-1笔交易 当前买入

买入一次就算一笔交易

递归边界

dfs(·, -1, ·) = -∞ 任何情况下，j都不能未负

dfs(-1, j, 0) = 0

dfs(-1, j, 1) = -∞

class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:n = len(prices)@cachedef dfs(i, j, hold):if j<0:return -infif i<0:return -inf if hold else 0if hold:# 当前持有# 买入时记作一次交易开始return max(dfs(i-1, j, 1), dfs(i-1, j-1, 0) - prices[i])# 当前未持有return max(dfs(i-1, j, 0), dfs(i-1, j, 1) + prices[i])return dfs(n-1, k, False)

递推代码

class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:n = len(prices)# 递推# 创建三维数组, 为什么k+2f = [[[0]*2 for _ in range(k+1)] for _ in range(n+1)]# 初始化：无论允许交易多少次，第0天开始时持有股票都是不可能的，初始化为-∞for i in range(k+1):f[0][i][1] = -inffor i, p in enumerate(prices):for j in range(1, k+1):# 未持有：什么也不做 || 卖出f[i+1][j][0] = max(f[i][j][0], f[i][j][1] + p)# 持有：什么也不做 || 买入f[i+1][j][1] = max(f[i][j][1], f[i][j-1][0] - p)return f[-1][-1][0]

恰好/至少交易k次，如何初始化

恰好完成k次初始化条件

f[0][1][0] = 0 第0天，恰好完成一次交易，当天买入当天卖出，利润为0

其余均初始化为 -inf

# 恰好
class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:# 递推n = len(prices)f = [[[-inf] * 2 for _ in range(k + 2)] for _ in range(n + 1)]# 只有第0天，恰好交易1次，当天买当天卖，未持有 利润为0f[0][1][0] = 0  # 只需改这里for i, p in enumerate(prices):for j in range(1, k + 2):f[i + 1][j][0] = max(f[i][j][0], f[i][j][1] + p)f[i + 1][j][1] = max(f[i][j][1], f[i][j - 1][0] - p)return f[-1][-1][0]class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:# 递推n = len(prices)# 恰好完成k次交易f = [[[-inf]*2 for _ in range(k+1)]for _ in range(n+1)]# 初始化

至少完成k次初始化条件

第0天

[0-k-1]均初始化为-inf

第k次初始化为0

# 至少
class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:# 递推n = len(prices)f = [[[-inf] * 2 for _ in range(k + 1)] for _ in range(n + 1)]# 初始化# 第0天开始，恰好交易0次，利润为0f[0][0][0] = 0for i, p in enumerate(prices):# 第i天结束时，恰好交易0次，未持有f[i + 1][0][0] = max(f[i][0][0], f[i][0][1] + p)f[i + 1][0][1] = max(f[i][0][1], f[i][0][0] - p)  # 无限次for j in range(1, k + 1):f[i + 1][j][0] = max(f[i][j][0], f[i][j][1] + p)f[i + 1][j][1] = max(f[i][j][1], f[i][j - 1][0] - p)return f[-1][-1][0]

121-买卖股票的最佳时机 - 只能交易一次 - 简单

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择某一天买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

class Solution:def maxProfit(self, prices: List[int]) -> int:'''维护到当前为止的最小价格 & 最大利润'''min_price = prices[0]max_profit = 0for p in prices:if p<min_price:min_price = pif max_profit<p-min_price:max_profit = p-min_pricereturn max_profit

如何用状态机来做？？等同于恰好交易一次的情况

注意初始化方式

class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)f = [[[0]*2 for _ in range(1+1)]for _ in range(n+1)]for i in range(1+1):f[0][i][1] = -inffor i, p in enumerate(prices):for j in range(1, 1+1):f[i+1][j][0] = max(f[i][j][0], f[i][j][1]+p)f[i+1][j][1] = max(f[i][j][1], f[i][j-1][0]-p)return f[-1][-1][0]

122-买卖股票的最佳时机Ⅱ-不限制交易次数-中等

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

class Solution:def maxProfit(self, prices: List[int]) -> int:'''不限制交易次数二维数组即可'''n = len(prices)f = [[0]*2 for _ in range(n+1)]# 初始化# 第0天开始时持有是不可能的f[0][1] = -inffor i, p in enumerate(prices):# 未持有f[i+1][0] = max(f[i][0], f[i][1]+p)# 持有f[i+1][1] = max(f[i][1], f[i][0]-p)return f[-1][0]

123-买卖股票的最佳时机Ⅲ-最多交易两次-困难

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

class Solution:def maxProfit(self, prices: List[int]) -> int:'''最多完成两笔交易'''n = len(prices)f = [[[0]*2 for _ in range(3)]for _ in range(n+1)]# 初始化# 第0天开始时持有是不可能的for i in range(3):f[0][i][1] = -inf# 递推for i, p in enumerate(prices):for j in range(1, 3):f[i+1][j][0] = max(f[i][j][0], f[i][j][1]+p)f[i+1][j][1] = max(f[i][j][1], f[i][j-1][0]-p)return f[-1][-1][0]

188-买卖股票的最佳时机Ⅳ-最多交易k次-困难

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:'''最多交易k次三维表示'''n = len(prices)f = [[[0]*2 for _ in range(k+1)]for _ in range(n+1)]# 初始化# 第0天开始时持有是不可能的for i in range(k+1):f[0][i][1] = -inf# 递推for i, p in enumerate(prices):for j in range(1, k+1):# 未持有f[i+1][j][0] = max(f[i][j][0], f[i][j][1]+p)f[i+1][j][1] = max(f[i][j][1], f[i][j-1][0]-p)return f[-1][-1][0]

309-买卖股票的最佳时机-含冷冻期, 不限制交易次数-中等-再看看

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

class Solution:def maxProfit(self, prices: List[int]) -> int:'''不限制交易次数二维即可卖出股票后，无法接着买入，冷冻期为一天但是买入之后，没有卖出限制'''n = len(prices)if n < 2:return 0# 初始化f = [[0] * 2 for _ in range(n+2)]  # 需要额外两个空间用于状态转移f[0][1] = -float('inf')  # 第0天开始时持有是不可能的f[1][1] = -prices[0]  # 第1天持有股票的情况# 第二天到第n天的情况for i in range(2, n+1):# 未持有：什么也不做 || 卖出，卖出无限制f[i][0] = max(f[i-1][0], f[i-1][1] + prices[i-1])# 持有：只能从昨天未持有状态买入f[i][1] = max(f[i-1][1], f[i-2][0] - prices[i-1])return f[-2][0]

714-买卖股票的最佳时机-含手续费-中等

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:'''不限制交易次数'''n = len(prices)f = [[0]* 2 for _ in range(n+1)]# 初始化f[0][1] = -inf# 只在买入时计算手续费for i, p in enumerate(prices):f[i+1][0] = max(f[i][0], f[i][1] + p)f[i+1][1] = max(f[i][1], f[i][0] - p - fee)return f[-1][0]