C++不知算法系列之计数排序算法的计数之巧-编程知识

1. 前言

计数排序是较简单的排序算法，其基本思想是利用数组索引号有序的原理。

如对如下的原始数组中的数据(元素)排序：

//原始数组
int nums[5]={9,1,7,6,8};

使用计数排序的基本思路如下：

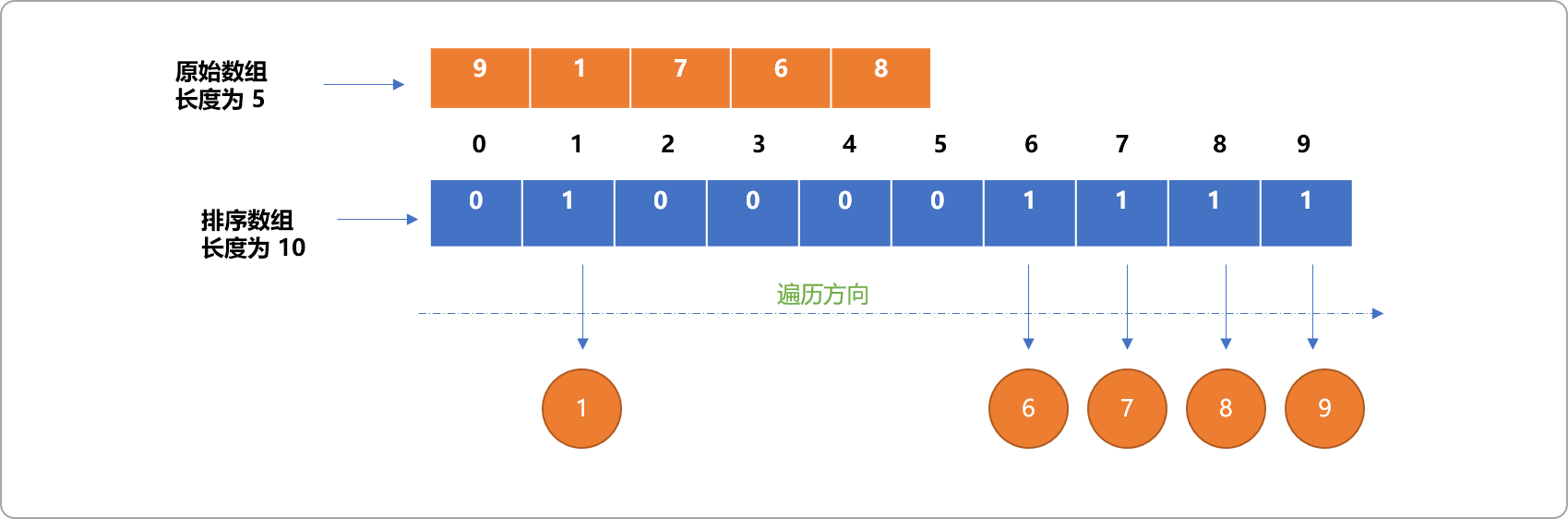
创建一个排序数组。数组的大小由原始数组的最大值决定，如原始数组的最大值为9，则排序数组的长度为 9+1。为什么排序数组的长度需要如此设置，后文将做解释。

int sortNums[10]={0}; //初始化值为 0

读取原始数组中的数据，以此数据作为排序数组的索引号，此数据出现的次数为排序数组的值。

这也解释了为什么排序数组的长度必须是原始数组中最大值加1。因为排序数组必须能为原始数组中的最大值提供索引号。

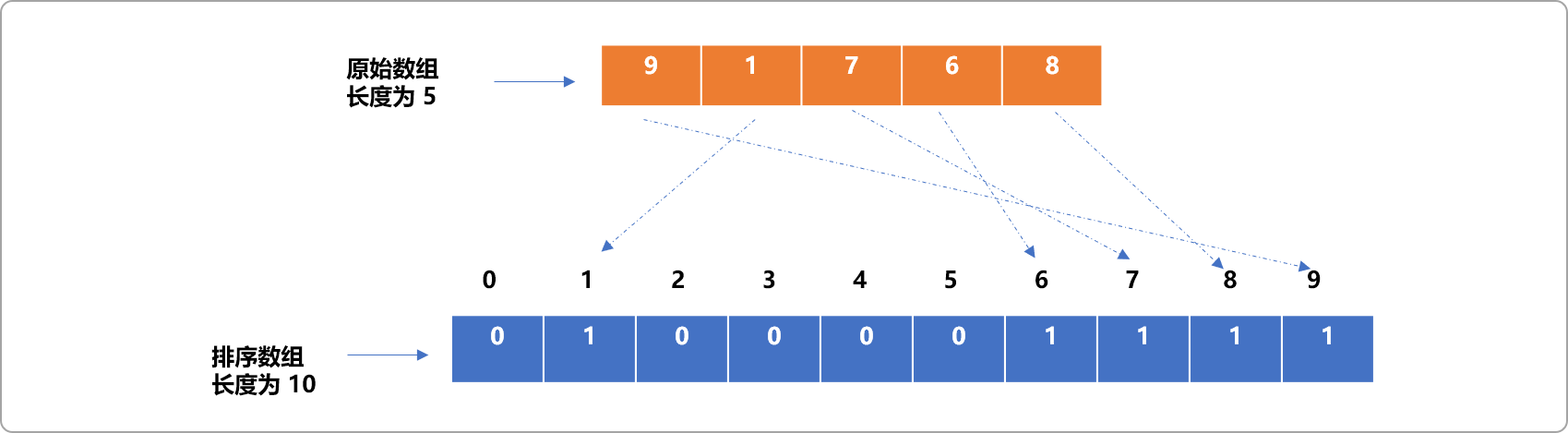
然后输出排序数组中的值不为 0的索引号。

编码实现：

#include <iostream>
using namespace std;
int main(int argc, char** argv) {//原数组int nums[5]= {9,1,7,6,8};//排序数组int sort[10]= {0};//转存for(int  i=0; i<5; i++) {sort[nums[i]]++;}//输出排序数组for(int i=0; i<10; i++) {if(sort[i]!=0)cout<<i<<"\t";}return 0;
}

输出结果：

通过上文简述可知：

计数排序的时间复杂度为O(n)，时间复杂度还算可观。
但是空间复杂度也是O(n)。相比较如冒泡、选择……排序算法，计数排序算法是以空间换取时间。

2. 两个问题

2.1 排序数组的长度

计数排序利用数组索引号的有序而对数据排序，所以，需要把原无序数组中的数据映射到排序数组的索引号上。于是，对排序数组的长度就会有一个最小值的约束，至少等于无序数组中的最大值加一。

如下面的无序数组：

int num[]={500,420,550};

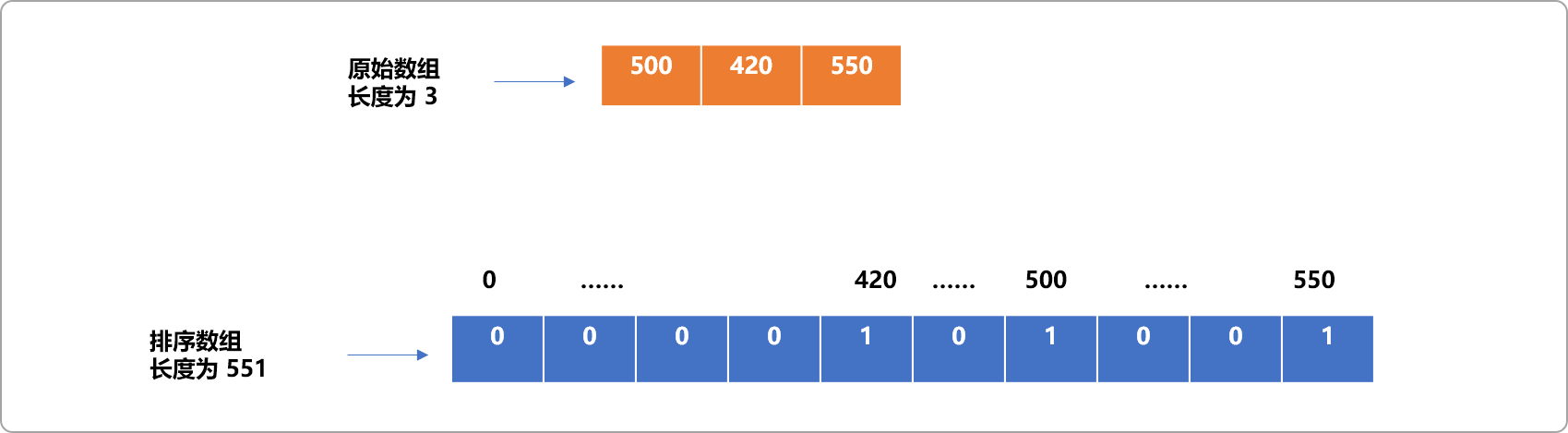
为了保证无序数组中的数据能映射到对应的索引号，则排序数组长度至少应该为 551。

int sort[551]={0};

而实际需要映射的数据只有 3 个，会导致排序数组空间浪费巨大，这也是计数排序缺点所在。

如下图所示：

如何解决此问题？

可以在创建排序数组时：

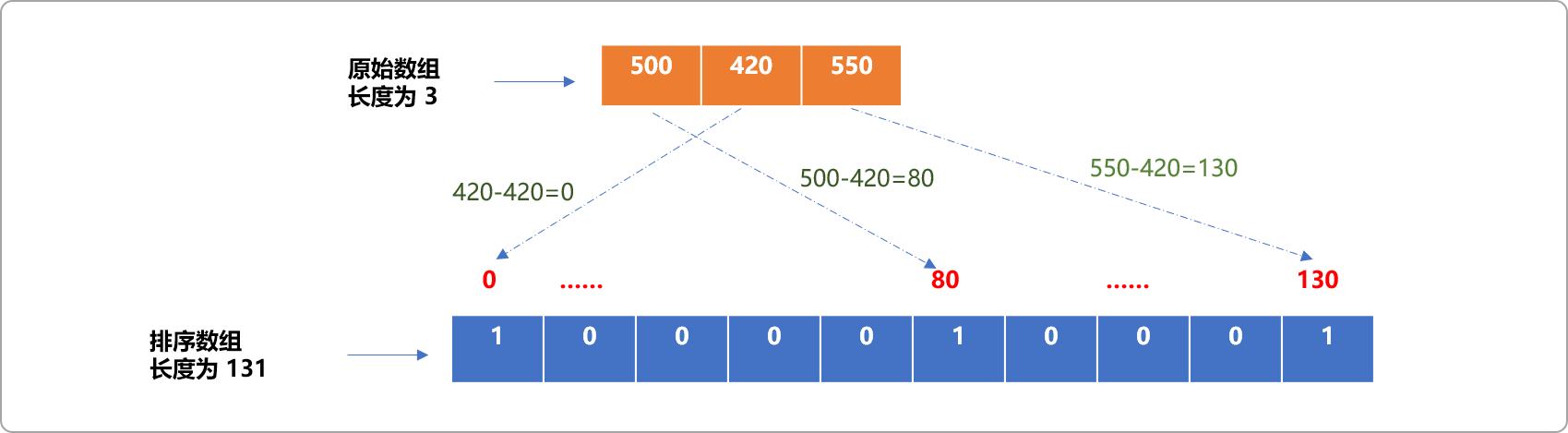
找到原始无序数组中的最大值（max）和最小值（min）。如上文无序数组的最大值为 550，最小值为420。
指定排序数组的长度为：max-min+1，即排序数组的长度为：131。
```
int sort[131]={0}; //初始值为0
```
无序数组到排序数组的映射规则：排序数组中的索引号=无序数组中的数据-最小值。

反之在遍历排序数组时：无序数组中的数据=排序数组中的索引号+最小值。

编码实现：

#include <iostream>
using namespace std;
int main(int argc, char** argv) {//原数组int nums[3]= {500,420,550};//硬代码求长度 int len=550-420+1; //排序数组int sort[len]= {0};//转存for(int  i=0; i<3; i++) {sort[nums[i]-420 ]++;}//输出排序数组for(int i=0; i<len; i++) {if(sort[i]!=0)cout<<(i+420)<<"\t";}return 0;
}

输出结果：

2.2 重复问题

如果无序数组中有重复数据，根据计数排序算法的映射原理，显然，相同数据会映射到排序数组的同一个位置。排序数组通过计数器方案对相同数据进行计数。这也是计数排序算法名称的由来。

如下图所示：无序数组中的 2 个 1和 2个9映射到了排序数组的同一个位置，排序数组的值记录了重复数据的多少。

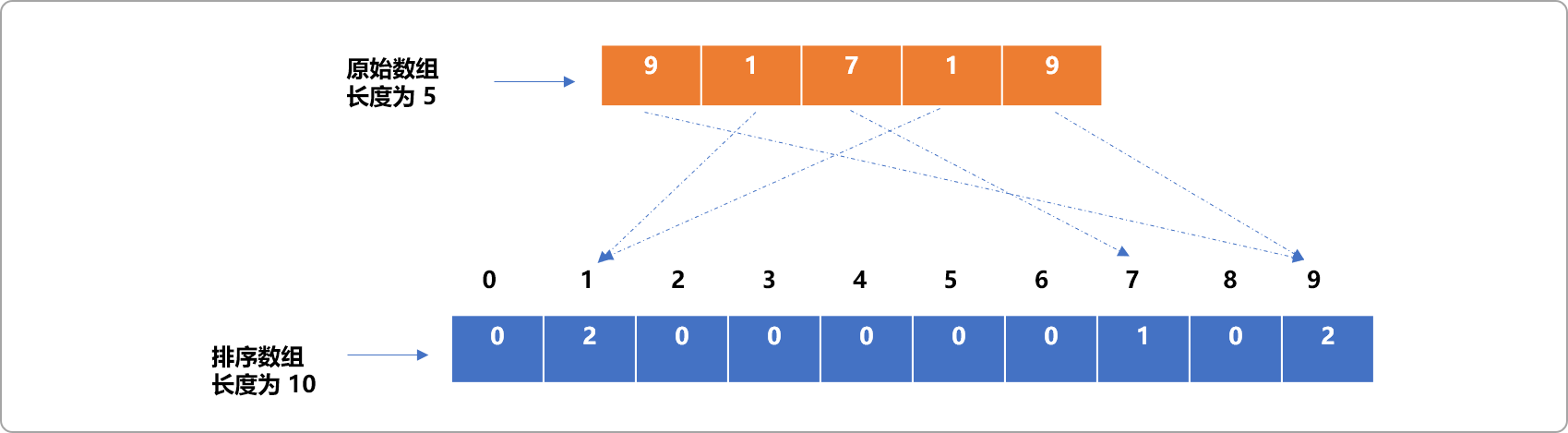
编码实现：

#include <iostream>
using namespace std;
int main(int argc, char** argv) {//原数组int nums[5]= {9,1,7,1,9};//排序数组int sort[10]= {0};//转存for(int  i=0; i<5; i++) {sort[nums[i] ]++;}//输出排序数组for(int i=0; i<10; ) {if(sort[i]!=0) {cout<<i<<"\t";sort[i]--;}else{i++;}}return 0;
}

输出结果：

此处只能对重复的数据计数，但无法得知重复数据的原始顺序。故，理论而言，计数排序算法是不稳定的。

有没有方案能输出时保留重复数据的原始先后顺序？

答案是：改造排序数组中的值，数组中的映射位置不再存储此索引号对应数据的个数，而是存储此索引号之前所有数据的个数。

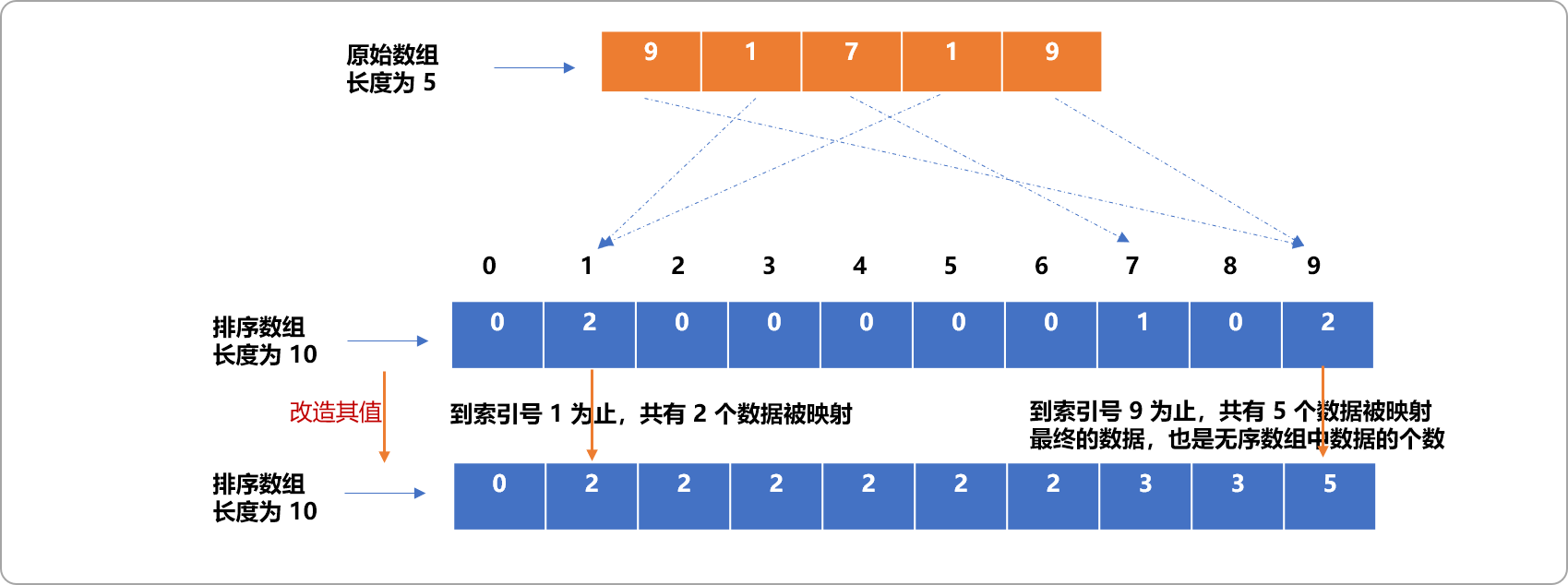
然后逆向遍历原始无序数组。用其值做为排序数组的索引号，找出存储在排序数组中的值然后减一，便知道此数据应该排在有序位置的第几位。

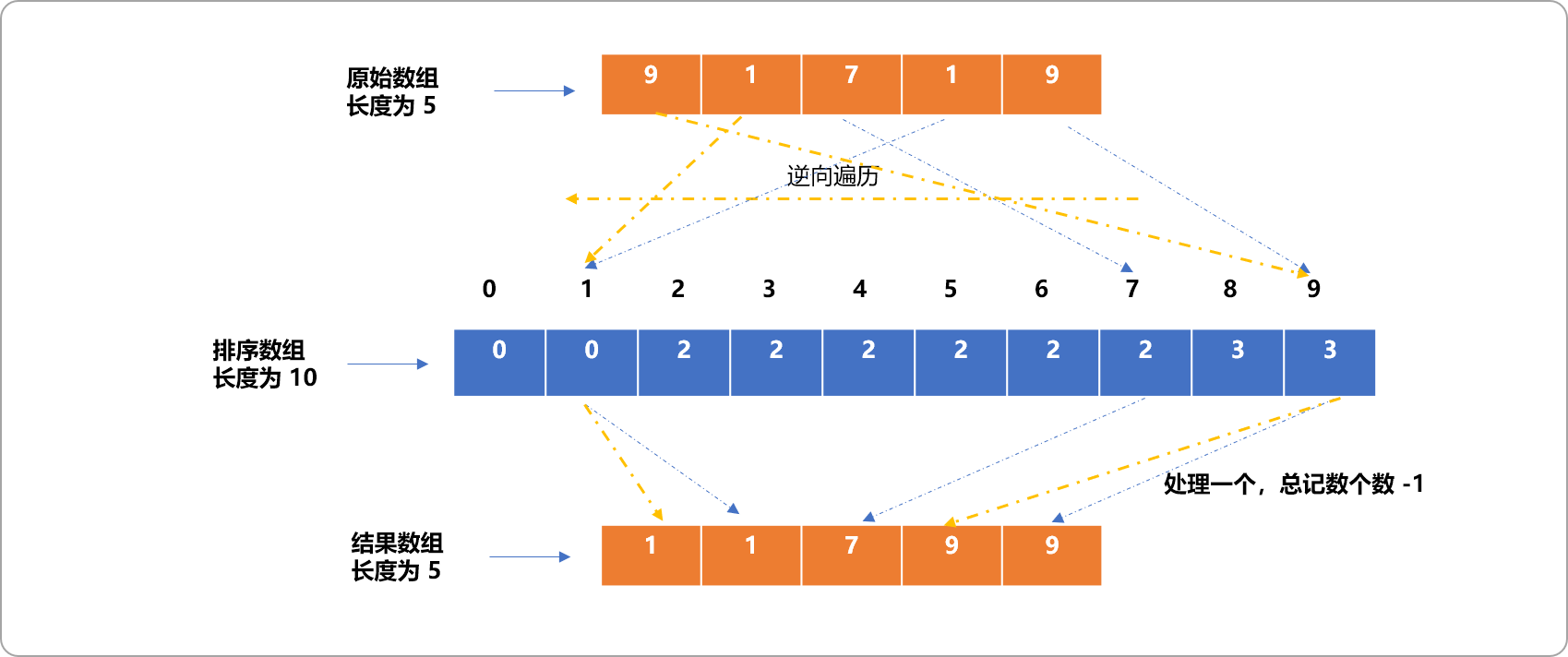
为什么要逆向遍历？

原因很简单，在映射时，是正向遍历，则无序数组中的第 1 个 9一定是先映射到排序数组的索引号为 9的位置，最后的一个 9是后映射到排序数组索引号为 9的位置。拿出来时，应该要遵循先进后出原则。

编码实现：

#include <iostream>
using namespace std;
int main(int argc, char** argv) {//原数组int nums[5]= {9,1,7,1,9};//排序数组int sort[10]= {0};//映射for(int  i=0; i<5; i++) {sort[nums[i] ]++;}//转值，排序数组中存储此索引号及之前已经映射的数据个数for(int i=1; i<10; i++) {sort[i]+=sort[i-1];}//结果数组int res[5]= {0};//逆向遍历原无序数组for(int i=4; i>=0; i-- ) {//无序数组中的数据作为排序数组的索引号，其值减一，即为 nums[i]的正确位置res[--sort[nums[i]]]=nums[i];	}//输出结果for(int i=0;i<5;i++){cout<<res[i]<<"\t";} return 0;
}

输出结果：

3. 完整的代码及应用

3.1 完整代码

上文对计数排序的实现流程做了分步讲解，综合基本思想以及其问题解决方案。下面是完整的代码。

#include <iostream>
using namespace std;
/*
*查找数组中的最大值、最小值
*/
pair<int,int> getMaxAndMin(int nums[],int size) {int mixn=nums[0];int maxn=nums[0];for(int i=1; i<size; i++) {if(nums[i]>maxn)maxn=nums[i];if(nums[i]<mixn)mixn=nums[i];}pair<int,int> p(mixn,maxn);return p;
}
/*
*计数排序
*/
void jsSort(int nums[],int size,int res[]) {pair<int,int> p=getMaxAndMin(nums,size);int mx=p.second;int mi=p.first;int sortLen=mx-mi+1;//排序数组int sort[ sortLen ]= {0};//映射且计数for(int i=0; i<size; i++) {sort[nums[i]-mi]++;}//计总数for(int i=1; i<sortLen; i++) {sort[i]+=sort[i-1];}//逆向遍历原数组int idx=0;for(int i=size-1; i>=0; i--) {//有序位置 idx= --sort[nums[i]-mi];res[idx]=nums[i];}
}
int main(int argc, char** argv) {int nums[5]= {9,1,7,1,9};int size=sizeof(nums)/4;//结果数组int res[size]= {0};jsSort(nums,size,res);for(int i=0; i<5; i++) {cout<<res[i]<<"\t";}return 0;
}

3.2 应用

2019-10-19的CSP-J试卷中有一道与计数排序算法有关的程序题。

题目描述：

(计数排序)计数排序是一个广泛使用的排序方法。下面的程序使用双关键字计数排序，将n对10000以内的整数，从小到大排序。
例如有三对整数(3,4)、(2,4)、(3.3)，那么排序之后应该是(2,4)、(3,3)、(3,4)。
输入第一行为n，接下来n行，第i行有两个数a[i]和b[i]，分别表示第 i对整数的第一关键字和第二关键字。从小到大排序后输出。
数据范围1≤n≤10^7，1≤a[i],b[i]≤10^4。
提示：应先对第二关键字排序，再对第一关键字排序。数组ord[]存储第二关键字排序的结果，数组res[]存储双关键字排序的结果。

试补全程序：

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int maxn=10000000;
const int maxs=10000;
int n;
unsigned a[maxn],b[maxn],res[maxn],ord[maxn];
unsigned cnt[maxs+1];
int main() {scanf("%d",&n);for(int i=0; i<n; ++i) {scanf("%d%d",&a[i],&b[i]);}memset(cnt,0,sizeof(cnt));for(int i=0; i<n; ++i)1 ; //使用 cnt 数据计数 for(int i=0; i<maxs; ++i) cnt[i+1]+=cnt[i];for(int i=0; i<n; ++i) 2 ;memset(cnt,0,sizeof(cnt));for(int i=0; i<n; i++) 3 ;for(int i=0; i<maxs; ++i) cnt[i+1]+=cnt[i];for(int i=n-1; i>=0; --i)4 ;for(int i=0; i<n; ++i)printf("%d %d\n",  5 );return 0;
}