模拟退火
必须要单独开一个专题来讲模拟退火了。
看到身边很多同学写的模退都是不标准的,步长没有随温度的降低而减小,只能叫随机爬山。
系统的学习模退是跟着 Acwing 的 yxc,他写的模退给人一看就有一种豁然开朗,神清气爽的感觉,让你惊叹天下竟然还有如此精妙的算法。
是的,优雅的模退写出来就是令人心旷神怡,而不是某些同学暴力算法的代言,像一坨屎山一样。
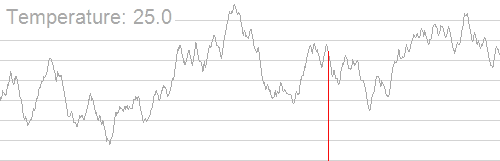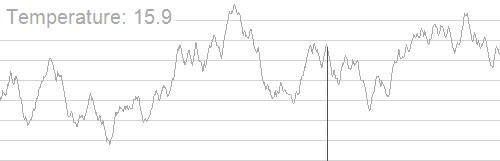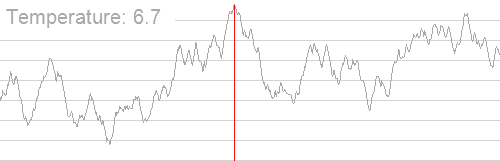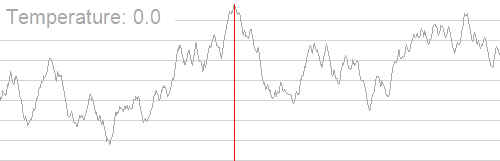
一谈起模退,我脑中就回想起这幅经典的动图,如他的定义一般精妙:
而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
可以发现波动程度逐渐变小,最后趋于稳定。
例题:星星还是树
其实就是费马点。
核心代码:
void simulate_anneal(){pdd cur(rand(0,1e4),rand(0,1e4));// 初始点(当前点)for (double t = 1e4; t > 1e-4; t *= 0.95){// 初始温度,终止温度,温度 * 衰减系数pdd rand_point(rand(cur.x - t,cur.x + t),rand(cur.y - t,cur.y + t));double delta = calc(rand_point) - calc(cur);if (exp(-delta / t) > rand(0,1)) cur = rand_point; // 满足条件则跳到新点}
}
关于 rand 函数
yxc 老师很巧妙的处理的直接使用rand()值域过小的问题。
double random(double l,double r){return (double) rand() / RAND_MAX * (r - l) + l;
}
当然我们有性能更好的 mt19937 也完全可以使用
mt19937 rnd(random_device{}());
int random(int l,int r){return rnd()%(r-l+1)+l;
}
关于 exp 函数
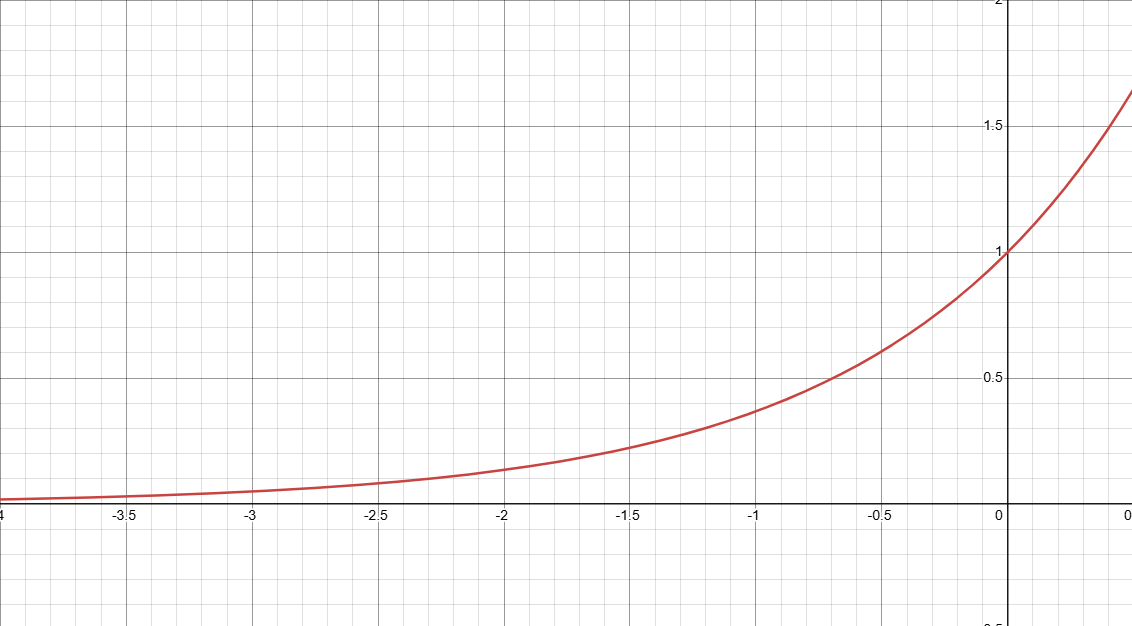
众所周知,模拟退火很重要的一个特点就是对于不优的解也以一定概率接受,防止陷入局部最优解的深坑中,定义 \(delt=contmeprorary-ans\) ,如果 \(ans\) 的值越小越优,那么以 \(exp(-delt/T)\) 的概率接受该解,注意如果 \(delt\) 为负数,则该函数值一定大于 \(1\) ,意味着一定接受。为整数则以一定概率接受。
关于 clock 函数
众做周知,我们在时间允许的情况下我们希望进行经可能多的模拟退火次数以保证答案的正确性,clock()/CLOCK_PER_CEC 可以帮我们解决这个问题。
for(;(double)clock()/CLOCK_PER_SEC;){fire();
}
完结撒花✿✿ヽ(°▽°)ノ✿
void fire(){double T=1e9,d=0.997;int x=rnd();ans=min(ans,check(x));while(T>1){// cout<<x<<endl;int nx=x+random(-T,T);long long temp=check(nx);double delt=temp-ans;if(exp((double)-delt/T)*T>random(0,T)){x=nx;}ans=min(temp,ans);T*=d;}
}