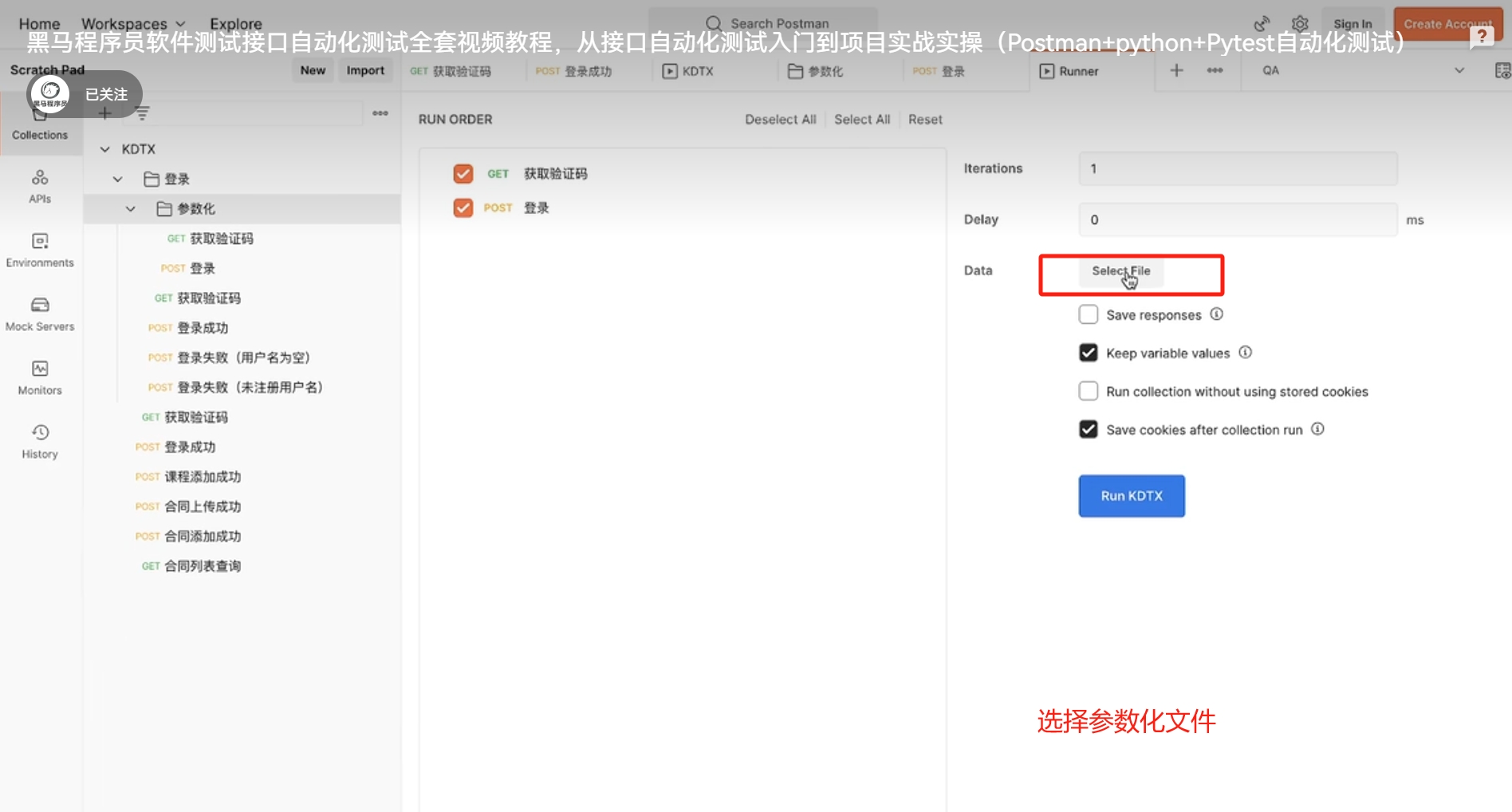
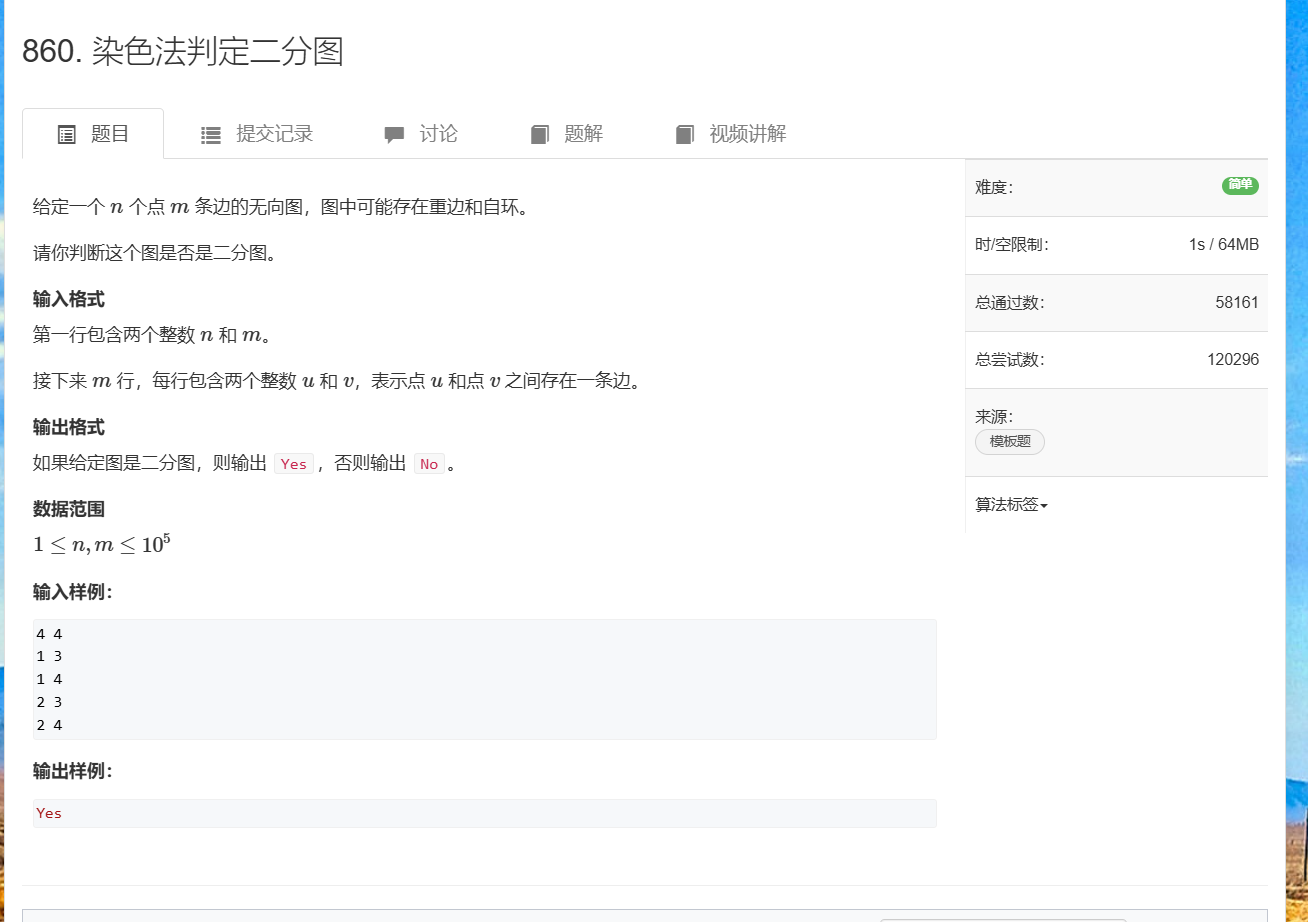
染色法判定二分图

染色法判定二分图

二分图：

1.当且仅当图中无奇数环

2.能且只能用两种颜色染色

 

#include <cstring>

#include <iostream>

#include <algorithm>

 

using namespace std;

 

const int N = 100010, M = 200010;

 

int n, m;

int h[N], e[M], ne[M], idx;

int color[N];

 

//邻接表

void add(int a, int b)

{

    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;

}

 

bool dfs(int u, int c)//深度优先遍历，u是当前点下标，c是当前点染的颜色

{

    color[u] = c;

 

    for (int i = h[u]; i != -1; i = ne[i])//遍历与u相邻的所有点

    {

        int j = e[i];

        if (!color[j])

        {//如果没染色就染成与u的颜色不同的颜色并且如果dfs为false就返回false

            if (!dfs(j, 3 - c)) return false;

        }

        else if (color[j] == c) return false;//如果染的颜色与u的颜色相同就返回false

    }

 

    return true;//剩余true

}

 

int main()

{

//邻接表存图

    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )

    {

        int a, b;

        scanf("%d%d", &a, &b);

        add(a, b), add(b, a);//无向图-->双向存！

    }

 

    bool flag = true;//true是不矛盾

    for (int i = 1; i <= n; i ++ )//n个顶点进行染色法

        if (!color[i])

        {//如果没有染色，就涂成1号色，如果dfs返回false说明就是有矛盾就flag=false退出循环

            if (!dfs(i, 1))

            {

                flag = false;

                break;

            }

        }

 

    if (flag) puts("Yes");

    else puts("No");

 

    return 0;

}