我的CSP、NOIP笔记随笔
零碎知识
-
prim kruskal dijkstra 使用贪心思想
-
斐波那契数列结论：\(\Sigma_{i=1}^{n}f(i)=f(n+2)-1\)
-
有些函数有单调性（单调递增或单调递减）
-
双指针法：用两个变量指向两个位置，要tail++,不要前面丢掉
-
组合数递推公式：\(C_m^n=C_m^{n-1}+C_{m-1}^{n-1}\)
-
费马小定理（求逆元）：p为质数时，有\(a^{p-1}\equiv1\ (mod\ p)\)
差分
可以用来将一个区间/矩阵改变大小
- 一维差分
- 起点加
- 终点后面减
cha[i]=a[i]-a[i-1]（差分）
a[i]=cha[i]+a[i-1]（前缀和）
a{1,5,7,3 ,6,9}
↓差分变换
cha{1,4,2,-4,3,3,-3}
↓将4~6增加3
cha{1,4,2,-4+3=-1,3,3,-3+3=0}
↓前缀和变换
a{1,5,7,6,9,12}
练习题：差分入门代码
#include <bits/stdc++.h>
int n,m,a[100001],cha[100001],u,v,w;
using namespace std;
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];cha[i]=a[i]-a[i-1];}cha[n+1]=0-a[n];cin>>m;for(int i=1;i<=m;i++){cin>>u>>v>>w;cha[u]+=w;//起点加一cha[v+1]-=w;//终点后面减}for(int i=1;i<=n;i++){a[i]=cha[i]+a[i-1];cout<<a[i]<<' ';}return 0;
}
- 二维差分
- 左上加
- 右上和左下减右下加
练习题：场馆布置代码
#include <bits/stdc++.h>
using namespace std;
int n,k,cha[1002][1002],a[1002][1002],con;
int main()
{scanf("%d%d",&n,&k);//修改差分数组for(int i=1;i<=n;i++){int lx,ly,rx,ry;scanf("%d%d%d%d",&lx,&ly,&rx,&ry);lx++,ly++,rx++,ry++;//防止越界//四个“带头人”cha[lx][ly]++;cha[rx][ly]--;cha[lx][ry]--;cha[rx][ry]++;}//还原差分数组for(int x=0;x<=1001;x++){for(int y=0;y<=1001;y++){a[x][y]=a[x-1][y]+a[x][y-1]-a[x-1][y-1]+cha[x][y];if(a[x][y]==k)con++;}}printf("%d",con);return 0;
}
/*暴力40分 TLE
#include <bits/stdc++.h>
using namespace std;
int n,k,a[1003][1003],con;
int main()
{scanf("%d%d",&n,&k);for(int i=1;i<=n;i++){int lx,ly,rx,ry;scanf("%d%d%d%d",&lx,&ly,&rx,&ry);for(int x=lx;x<=rx-1;x++){for(int y=ly;y<=ry-1;y++){a[x][y]++;}}}for(int x=0;x<=1000;x++){for(int y=0;y<=1000;y++){if(a[x][y]==k)con++;}}printf("%d",con);return 0;
}
*/
递推关系
-
算与推
算好一些（快），但是推好理解。 -
举例-一维
- 斐波那契
- 直线分平面(二阶等差数列)
- 走台阶（斐波那契变形\(A(i)=A(i-1)+A(i-2)+A(i-3)+...\)）
- 错排问题
n-1个错了，第n个随便交换，都全错了；
n-2个对了，第n个插入对的，都错了。
\(W(n)=(n-1)\times(W(n-1)+W(n-2))\)
- 全排列问题正求、反求
-
举例-二维
-
杨辉三角
#include <bits/stdc++.h> using namespace std; const long long MOD=2147483648; long long a[4001][4001],sum; int n; int main() { cin>>n; for(int i=1;i<=n;i++) {a[i][1]=1;a[i][i]=1;for(int j=1;i<=j;j++)a[i][j]=(a[i-1][j-1]+a[i-1][j])%MOD; } cout<<a[n][n]; return 0; } -
数字拆分：n分成m个数
f(10,3)：含有1：f(9,2) ; 不含1：f(7,3)
\(f(n,m)=f(n-1,m-1)+f(n-m,m)\)(类似杨辉三角)#include <bits/stdc++.h> using namespace std; const long long MOD=2147483648; long long a[4001][4001],sum; int n; int main() { cin>>n; for(int i=1;i<=n;i++) {a[i][1]=1;a[i][i]=1;for(int j=2;j<=i-1;j++)a[i][j]=(a[i-1][j-1]+a[i-j][j])%MOD; } for(int i=2;i<=n;i++)sum=(sum+a[n][i])%MOD; cout<<sum; return 0; }树状数组
-
| 数据结构 | 数组 | 前缀和数组 |
|---|---|---|
| 修改 | \(O(1)\) | \(O(n)\) |
| 查询 | \(O(n)\) | \(O(1)\) |
| 总效率 | \(O(mn)\) | \(O(mn)\) |
~鱼和熊掌不可兼得~：分块前缀和、树状数组（平衡）
| 数据结构 | 分块前缀和 | 树状数组 |
|---|---|---|
| 修改 | \(O(\sqrt n)\) | \(O(\log_2n)\) |
| 查询 | \(O(\sqrt n)\) | \(O(\log_2n)\) |
| 总效率 | \(O(m\sqrt n)\) | \(O(m\log_2n)\) |
- 分块前缀和：每k个分成一段。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+1;
int a[N],s[N];//a原数组，q分段前缀和数组
int main()
{//输入n,a //构成分段 int k=sqrt(n); for(int i=1;i<=n;i+=k){s[i]=a[i];for(int j=i+1;j<=i+k-1;j++){s[j]=s[j-1]+a[j];} } //修改 a[x]+=y;//找x的块[i,i+k-1] O(n/k)//修改x和后面的元素 O(k)//查询a[x]+...+a[y]//找x和y的块（设x的为i,y的为j）//x->[if,if+k-1]-需要-->[x,if+k-1] //中间的就是分段前缀和加一加 //x->[jf,jf+k-1]-需要-->[y,jf+k-1] return 0;
}
-
lowbit(x)：二进制数最后一个1,能够整除x的最大的2的幂
\(lowbit(x)= x\&-x\)//例子 x :1011000 ~x :0100111 ~x+1:0101000 (-x) x&-x: 1000 -
树状数组：奇数号位加到偶数号位（要覆盖）
flowchart LR
subgraph 树状数组构成图direction TBsubgraph 1endsubgraph 2endsubgraph 3endsubgraph 4endsubgraph 5endsubgraph 6endsubgraph 7endsubgraph 8endsubgraph 9endsubgraph 10endsubgraph 11endsubgraph 12endsubgraph 13endsubgraph 14endsubgraph 15endsubgraph 16endsubgraph 1-2endsubgraph 3-4endsubgraph 5-6endsubgraph 7-8endsubgraph 9-10endsubgraph 11-12endsubgraph 13-14endsubgraph 15-16endsubgraph 1-4endsubgraph 5-8endsubgraph 9-12endsubgraph 13-16endsubgraph 1-8endsubgraph 9-16endsubgraph 1-16end
end
1 & 2 --- 1-2
3 & 4 --- 3-4
5 & 6 --- 5-6
7 & 8 ---7-8
9 & 10 --- 9-10
11 & 12 --- 11-12
13 & 14 --- 13-14
15 & 16 --- 15-16
1-2 & 3-4 --- 1-4
5-6 & 7-8 --- 5-8
9-10 & 11-12 ---9-12
13-14 & 15-16 --- 13-16
1-4 & 5-8 --- 1-8
9-12 & 13-16 --- 9-16
1-8 & 9-16 --- 1-16
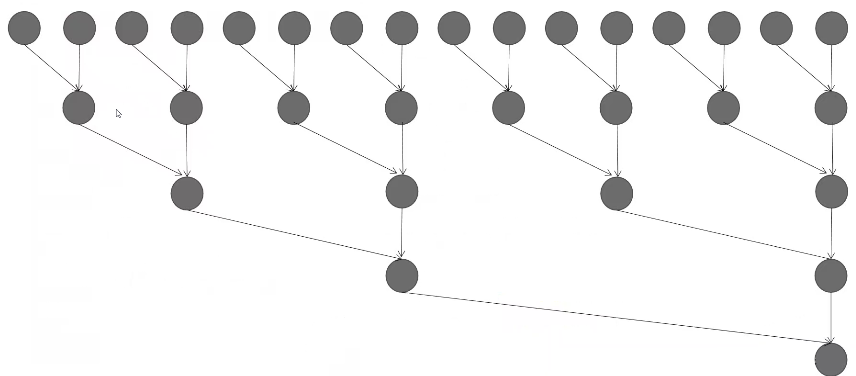
树状数组b[x]:由a[x]向前lowbit(x)个的和
\(b[x]=a[x-lowbit(x)+1]+...+a[x]\)
-
构建 \(O(n\log_2n)\)或\(O(n)\)
-
查询 \(O(\log_2n)\)
-
单点更新 \(O(\log_2n)\)
- 题目1&2： 树状数组1（单点修改，区间查询），树状数组2（区间修改，单点查询）
#include <bits/stdc++.h> using namespace std; #define MY_N_ 500005 class Binary_Indexed_Trees1{//单点修改+区间查询的树状数组类 private: int _t[MY_N_],_n; int _lowbit(int x)//lowbit { return x&(-x); } public: void build(int a[],int n)//O(n)建树 {_n=n;int lb;for(int i=1;i<=_n;i++){_t[i]+=a[i];lb=i+_lowbit(i);if(lb<=_n)_t[lb]+=_t[i];}return ; } void update(int x,int k)//O(log2n)单点修改 {for(;x<=_n;x+=_lowbit(x)){_t[x]+=k;}return ; } int query(int x)//O(log2n)区间查询 {int sum=0;for(;x;x-=_lowbit(x)){sum+=_t[x];}return sum; } }bit1; class Binary_Indexed_Trees2{//区间修改+单点查询的树状数组类 private: int _t[MY_N_],_n; int _lowbit(int x)//lowbit { return x&(-x); } public: void build(int a[],int n)//O(n)建树 {_n=n+1;int lb;for(int i=1;i<=_n;i++){_t[i]+=(a[i]-a[i-1]);lb=i+_lowbit(i);if(lb<=_n)_t[lb]+=_t[i];}return ; } void update(int l,int r,int k)//O(log2n)区间修改 {for(;l<=_n;l+=_lowbit(l)){_t[l]+=k;}for(r=r+1;r<=_n;r+=_lowbit(r)){_t[r]-=k;}return ; } int query(int x)//O(log2n)单点查询 {int sum=0;for(;x;x-=_lowbit(x)){sum+=_t[x];}return sum; } }bit2; int n,m,a[500005]; int solve1(){//单点修改+区间查询的树状数组的调用代码 scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) {scanf("%d",&a[i]); } bit1.build(a,n); int op,x,y; for(int i=1;i<=m;i++) {scanf("%d%d%d",&op,&x,&y);if(op==1){bit1.update(x,y);}else if(op==2){printf("%d\n",bit1.query(y)-bit1.query(x-1));} } return 0; } int solve2(){//区间修改+单点查询的树状数组的调用代码 scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) {scanf("%d",&a[i]); } bit2.build(a,n); int op,x,y,k; for(int i=1;i<=m;i++) {scanf("%d",&op);if(op==1){scanf("%d%d%d",&x,&y,&k);bit2.update(x,y,k);}else if(op==2){scanf("%d",&x);printf("%d\n",bit2.query(x));} } return 0; } int main() { // return solve1(); return solve2(); }- 题目3： A Simple Problem with Integers（区间修改，区间查询）
//#include <bits/stdc++.h>
#include<iostream>
#include<cstdio>
using namespace std;#define MY_N_ 100005
class Binary_Indexed_Trees3{//区间修改+区间查询的树状数组类
/*
I. 维护差分值的树状数组，区间修改可改为单点修改
II.区间查询如下： 设原数组为a[],差分数组为d[]则a[i]=sigma(j=1~i)d[j] 前x项的和s[x]=sigma(i=1~x)a[i]=sigma(i=1~x)sigma(j=1~i)d[j] =sigma(i=1~x)d[i]*(n-i+1)=(n+1)*sigma(i=1~x)d[i] - sigma(i=1~x)d[i]*i维护差分值的树状数组 维护差分值*编号的树状数组
*/
private:int _t[MY_N_],_c[MY_N_],_n;int _lowbit(int x)//lowbit { return x&(-x);}
public:void build(int a[],int n)//O(n)建树 {_n=n+1;int lb;for(int i=1;i<=_n;i++){_t[i]+=(a[i]-a[i-1]);_c[i]+=(a[i]-a[i-1])*i;lb=i+_lowbit(i);if(lb<=_n)_t[lb]+=_t[i],_c[lb]+=_c[i];}return ;}void update(int l,int r,int k)//O(log2n)区间修改 {int tl=l,tr=r+1;for(;l<=_n;l+=_lowbit(l)){_t[l]+=k;_c[l]+=k*tl;}for(r=r+1;r<=_n;r+=_lowbit(r)){_t[r]-=k;_c[r]-=k*tr;}return ;}int query(int x)//O(log2n)区间查询 1~x{int sum=0,sum1=0,tx=x;for(;x;x-=_lowbit(x)){sum+=_t[x];sum1+=_c[x];}return sum*(tx+1)-sum1;}
}bit3;int n,m,a[100005];
int solve3()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}bit3.build(a,n);int op,x,y,k;char s[5];for(int i=1;i<=m;i++){scanf("%s",s);if(s[0]=='C'){scanf("%d%d%d",&x,&y,&k);bit3.update(x,y,k);}else if(s[0]=='Q'){scanf("%d%d",&x,&y);printf("%d\n",bit3.query(y)-bit3.query(x-1));}}return 0;
}
int main()
{return solve3();
}
-
题目4：守墓人（综合所有操作）
假设d[]为a[]的差分数组，s[]为a[]的前缀和数组
\(s[k] =a[1]+a[2]+ ...+a[k] \\ \ \ \ =(d[1])+(d[1]+d[2])+... +(d[1]+d[2]+... +d[k]) \\ \ \ \ =kd[1]+(k-1 )d[2]+(k-2)d[3]+ ...=d[k]\\ \ \ \ =(k+ 1)(d[1]+d[2]+... +d[k]) - (1d[1]+2d[2]+... +kd[k])\) -
题目5：小鱼比可爱（数据范围太小，需要增加到\(n<=10^5\)）
线段树
-
查询最值 \(log_2n\)
-
题目1：借教室
-
思路
-
建树（剩余教室最小值）
-
每个订单开始减（到负的输出）
- 样例分析
-
-
代码（因为线段树的方法限制只有90或95分）：
#include <bits/stdc++.h> using namespace std; const int N=1e6+5; struct node { int l,r,minx,lz;//维护剩余教室最小值 }tree[4*N]; int a[N]; void buildtree(int k,int l,int r)//建树 { tree[k].l=l; tree[k].r=r; if(l==r) {tree[k].minx=a[l];return ; } int mid=(l+r)>>1; buildtree(k<<1,l,mid);//k<<1=k*2 buildtree(k<<1|1,mid+1,r);//k<<1|1=k*2+1 tree[k].minx=min(tree[k<<1].minx,tree[k<<1|1].minx); } void pushdown(int k) { if(tree[k].lz!=0) {tree[k<<1].minx-=tree[k].lz;tree[k<<1|1].minx-=tree[k].lz;tree[k<<1].lz+=tree[k].lz;tree[k<<1|1].lz+=tree[k].lz;tree[k].lz=0; } } void update(int k,int L,int R,int key) { if(tree[k].l>=L&&tree[k].r<=R) {tree[k].minx-=key;tree[k].lz+=key;//懒标记：累计修改了多少 return ; } pushdown(k);//下放 int mid=(tree[k].l+tree[k].r)>>1; if(L<=mid)update(k<<1,L,R,key); if(R>mid)update(k<<1|1,L,R,key); tree[k].minx=min(tree[k<<1].minx,tree[k<<1|1].minx); } int main() { int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) {scanf("%d",&a[i]); } buildtree(1,1,n); for(int i=1;i<=m;i++) {int d,s,t;scanf("%d%d%d",&d,&s,&t);update(1,s,t,d);if(tree[1].minx<0){printf("-1\n%d",i);return 0;} } printf("0"); return 0; }
-
最短路练习
- 洛谷P3906 Geodetic集合
#include <bits/stdc++.h>
using namespace std;
const int N=45;
vector<int> G[N];
int n,m,k,dis1[N],dis2[N],book[N];
void bfs(int s,int dis[])
{memset(dis,0x3f,sizeof(dis));memset(book,0,sizeof(book));queue<int> q;q.push(s);book[s]=1;dis[s]=0;while(!q.empty()){int u=q.front();q.pop();for(int i=0;i<G[u].size();i++){int v=G[u][i];if(book[v]==1) continue;q.push(v);book[v]=1;dis[v]=dis[u]+1; }}return ;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);G[u].push_back(v);G[v].push_back(u);}scanf("%d",&k);for(int i=1;i<=k;i++){int s,e;scanf("%d%d",&s,&e);bfs(s,dis1);bfs(e,dis2);for(int j=1;j<=n;j++){if(dis1[j]+dis2[j]==dis1[e]){cout<<j<<' ';}} cout<<endl;}return 0;
}
- 洛谷-P1144 最短路计数
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5,MOD=100003;
vector<int> G[N];
int n,m,k,dis[N],cnt[N],book[N];
void bfs(int s)
{memset(dis,0x3f,sizeof(dis));memset(book,0,sizeof(book));queue<int> q;q.push(s);book[s]=1;dis[s]=0;while(!q.empty()){int u=q.front();q.pop();for(int i=0;i<G[u].size();i++){int v=G[u][i];if(book[v]==1) continue;q.push(v);book[v]=1;dis[v]=dis[u]+1; }}return ;
}
void solve(int s)
{memset(cnt,0,sizeof(cnt));memset(book,0,sizeof(book));queue<int> q;q.push(s);book[s]=1;cnt[s]=1;while(!q.empty()){int u=q.front();q.pop();for(int i=0;i<G[u].size();i++){int v=G[u][i];if(dis[u]+1==dis[v]){cnt[v]=(cnt[v]+cnt[u])%MOD;if(book[v]==1) continue;q.push(v);book[v]=1;}}}return ;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);G[u].push_back(v);G[v].push_back(u);}bfs(1);solve(1);for(int i=1;i<=n;i++){if(dis[i]==0x3f3f3f)cout<<0<<endl;else cout<<cnt[i]%MOD<<endl;}return 0;
}
拓扑排序
- 便利入读为0的边，入队
- 如果队非空，取队首它就结束了
- 从队首出发 终点的入度-1，如果终点入度为0就入队
- 重复2,3直到队为空。
- 练习 P1807最长路
#include <bits/stdc++.h>
using namespace std;
struct node
{int v,w;node(int a,int b):v(a),w(b){ }
};
vector<node> edge[1501];
int q[1501],head=1,tail=1;
int n,m,ind[1501],dis[1501],ok[1501];
void topsort()
{ ok[1]=1;for(int i=1;i<=n;i++)if(ind[i]==0)q[tail++]=i;while(head<tail){int u=q[head++];for(int i=0;i<edge[u].size();i++){int v=edge[u][i].v,w=edge[u][i].w;ind[v]--;if(dis[v]<dis[u]+w&&ok[u]){ok[v]=1;dis[v]=dis[u]+w;}if(ind[v]==0) q[tail++]=v;}}return ;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);edge[u].push_back(node(v,w));ind[v]++;}topsort();
// cout<<"_______---"<<endl;
// for(int u=1;u<=n;u++)
// for(int i=0;i<edge[u].size();i++)
// {
// int v=edge[u][i].v,w=edge[u][i].w;
// cout<<u<<' '<<v<<' '<<w<<endl;
// }
// for(int i=1;i<tail;i++)
// cout<<q[i]<<' ';
// cout<<"_______---"<<endl;if(dis[n]==0)printf("-1");elseprintf("%d",dis[n]);return 0;
}
-
测评数据#3
in:
15 100
2 6 190
6 10 170
6 7 101
4 9 29
9 10 154
9 13 129
1 13 106
6 15 72
1 10 177
4 13 112
1 5 31
11 13 191
8 13 57
3 4 183
6 15 9
9 12 188
1 12 162
6 11 159
4 11 41
3 6 91
12 15 20
2 10 53
1 9 127
3 9 93
4 14 7
6 15 119
12 14 103
1 11 93
4 14 187
5 9 48
1 4 18
1 12 198
12 15 198
5 8 72
13 14 92
9 15 190
3 9 191
1 14 156
6 9 69
3 7 92
5 12 88
7 10 55
3 11 88
2 13 157
10 12 189
3 11 60
4 5 196
2 12 105
1 14 112
2 5 196
3 5 161
1 6 173
12 15 59
6 10 186
4 5 22
3 11 77
5 15 24
10 15 172
3 8 118
3 14 70
9 14 192
6 13 80
3 12 181
3 8 22
12 15 100
3 6 13
6 12 67
5 9 102
2 12 78
8 11 87
3 11 115
4 10 109
8 13 74
1 8 29
9 14 120
3 8 123
4 11 190
4 5 103
1 4 193
10 11 140
2 10 35
2 13 150
7 8 137
3 13 96
6 12 23
5 8 96
6 9 162
3 9 7
9 12 35
3 4 75
1 10 25
1 14 79
7 14 134
3 15 156
3 4 81
1 14 41
3 12 77
6 14 75
3 9 10
6 15 31
out:
1032欧拉路练习
-
P2731 [USACO3.3]骑马修栅栏 Riding the Fences
//90分TLE版本
#include <bits/stdc++.h>
using namespace std;
int n=500,m,edge[501][501],d[501];
stack<int> ans;
void dfs(int u)
{for(int v=1;v<=n;v++){if(edge[u][v]){edge[u][v]--;edge[v][u]--;dfs(v);}}ans.push(u);
}
int main()
{scanf("%d",&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);edge[u][v]++;edge[v][u]++;d[u]++;d[v]++;}/*判断是否有欧拉路，此题不需要 int cnt=0;//度为奇数的点的个数 for(int i=1;i<=n;i++){if(d[i]%2==1)cnt++;} if(cnt!=0&&cnt!=2){//没有欧拉路return 0; } */int s=1;for(int i=1;i<=n;i++){if(d[i]%2==1){s=i;break;}} dfs(s);while(!ans.empty()){cout<<ans.top()<<endl;ans.pop();}return 0;
}
- P7771 【模板】欧拉路径
#include <bits/stdc++.h>
using namespace std;
struct node
{int v,flag;node(int a,int b):v(a),flag(b){ }
};
vector<node> edge[100001];
int n,m,rd[100001],cd[100001];
stack<int> ans;
bool cmp(node x,node y)
{return x.v<y.v;
}
void dfs(int u)
{for(int i=0;i<edge[u].size();i++){if(!edge[u][i].flag){edge[u][i].flag=1;dfs(edge[u][i].v);}}ans.push(u);
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);edge[u].push_back(node(v,0));rd[v]++;cd[u]++;}int rjcdy=0,cjrdy=0;for(int i=1;i<=n;i++){if(rd[i]-cd[i]==1)rjcdy++;if(cd[i]-rd[i]==1)cjrdy++;} if(rjcdy>1||cjrdy>1){cout<<"No";return 0; } int s=1;for(int i=1;i<=n;i++){if(cd[i]-rd[i]==1){s=i;break;}} for(int i=1;i<=n;i++){sort(edge[i].begin(),edge[i].end(),cmp);}dfs(s);while(!ans.empty()){printf("%d ",ans.top());ans.pop();}return 0;
}
//AC版本
#include <bits/stdc++.h>
using namespace std;
vector<int> edge[100001];
int n,m,rd[100001],cd[100001];
stack<int> ans;
bool cmp(int x,int y)
{return x>y;
}
void dfs(int u)
{while(edge[u].size()>0){int v=edge[u][edge[u].size()-1];edge[u].pop_back();dfs(v);}ans.push(u);
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);edge[u].push_back(v);rd[v]++;cd[u]++;}int rjcdy=0,cjrdy=0;for(int i=1;i<=n;i++){if(rd[i]-cd[i]==1)rjcdy++;if(cd[i]-rd[i]==1)cjrdy++;} if(rjcdy>1||cjrdy>1){cout<<"No";return 0; } int s=1;for(int i=1;i<=n;i++){if(cd[i]-rd[i]==1){s=i;break;}} for(int i=1;i<=n;i++){sort(edge[i].begin(),edge[i].end(),cmp);}dfs(s);while(!ans.empty()){printf("%d ",ans.top());ans.pop();}return 0;
}
