基础图论
图的存储方式
无向边可以拆成两条有向边
1. 邻接矩阵
邻接矩阵:若 \(𝑖→𝑗\) 存在有向边,则令矩阵 \(𝐴[𝑖][𝑗]=1\)。
遍历一个点的所有出边是 \(𝑂(𝑛)\) 的。
空间复杂度 \(𝑂(𝑛^2 )\)。
总结:复杂度太高,尽量不使用
bool hasEdge[MAXN][MAXN];
int n,m;
signed main(){cin>>n>>m;for(int i=0,u,v;i<m;i++){int u, v;cin >> u >> v;hasEdge[u][v]=true;}for(int v=0;v<n;v++){if(hasEdge[u][v]){//......}}return 0;
}2. 邻接表
方法:每个节点开一个链表,存储所有连出去的边。
遍历一个点 \(𝑥\) 的所有出边是 \(𝑂(𝑜𝑢𝑡_𝑥 )\) 的,其中 \(𝑜𝑢𝑡_𝑥\) 为 \(𝑥\) 的出度。
空间复杂度 \(𝑂(𝑛+𝑚)\)。
const int N = 1e5 + 10, M = 1e5 + 10;
int head[N], nxt[M], point[M];
int n, m, totEdge;
void addEdge(int u, int v){totEdge++;nxt[totEdge]= head[u];point[totEdge]=v;head[u]= totEdge;
}
int main(){cin >> n >> m;for(int i=0;i < m; i++){int u, v;cin >> u >> v;addEdge(u, v);}for(int i= head[u]; i; i = nxt[i]){int v = point[i];//......}return 0;
}
3. vector
每个节点开一个 vector ,存储所有连出去边的终点。
遍历一个点 \(𝑥\) 的所有出边是 \(𝑂(𝑜𝑢𝑡_𝑥 )\) 的,其中 \(𝑜𝑢𝑡_𝑥\) 为 \(𝑥\) 的出度。
空间复杂度 \(𝑂(𝑛+𝑚)\)。
实际上与邻接表类似。
int n,m;
vector<int> nextPoints[MAXN];
signed main(){cin>>n>>m;for(int i=0,u,v;i<m;i++){cin>>u>>v;nextPoints[u].push_back(v);}for(int v=0;v<n;v++){//......}return 0;
}
总结:使用邻接表或 vector 来存,复杂度小
DFS 找环
维护一个 DFS 的栈。
在枚举下一个点时检查是否已在栈中。
复杂度 \(𝑂(𝑛+𝑚)\)。
如果是无向图,由于需要排除大小为 \(2\) 的环,可以记录 \(𝑥\) 的上一个点 \(𝑙𝑎𝑠𝑡\),\(𝑦=𝑙𝑎𝑠𝑡\) 时直接跳过。
const int MAXN=100005;
bool vis[MAXN],inStack[MAXN];
int n,m;
vector<int> nextPoints[MAXN];
bool dfs(int x){vis[x]= true;inStack[x]= true;bool result = false;for(auto y: nextPoints[x]){if(inStack[y])result = true;if(!vis[y])result |= dfs(y);}inStack[x]= false;return result;
}
signed main(){cin >>n >> m;for(int i=0,u, v; i< m; i++){cin >>u >> v;nextPoints[u].push_back(v);}bool hasLoop = false;for(int i=0;i<n; i++){if(!vis[i])hasLoop |= dfs(i);}return 0;
}
图的连通性问题
问题:加入 \(𝑚\) 条边,问两点之间是否连通。
可以使用并查集维护。
int fa[N];
int n, m;
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int u, int v){fa[find(u)]= find(v);
}
bool isConnected(int u,int v){return find(u)== find(v);
}
int main(){cin >> n >> m;for(int i = 0; i < n; i++){fa[i] = i;}for(int i = 0; i < m; i++){int u, v;cin >> u >> v;if(!isconnected(u, v))merge(u, v);}return 0;
}
并查集
适用于:合并两个连通块、查询两个节点是否位于同一连通块问题
对于每个节点 \(𝑥\),记录所在集合的代表元素 \(𝑓[𝑥]\)。如果在节点 \(𝑥\) 与 \(𝑦\) 之间连一条边,只需要令 \(𝑓[𝑓[𝑥]]=𝑓[𝑦]\)。
优化
考虑优化
方法:路径压缩,按秩合并。
只用其一则复杂度为 \(𝑂(𝑛 \log 𝑛 )\),二者并用复杂度为 \(O(nα(n))\)(都为均摊)。
注意:
int find(int x){if(f[x] == x){return x;}return f[x] = find(f[x]);// 此处为路径压缩
}
void merge(int x4, int y){x = find(x), y = find(y);if(size[x] > size[y]){swap(x, y); }f[x] = y, size[y] += size[x];// 此处为按秩合并
}
T1 程序自动分析
问题简述:
给定 \(𝑛\) 个变量 \(𝑥_𝑖\),以及 \(𝑚\) 个限制,形如 $𝑥_𝑖=𝑥_𝑗 $ 或者 \(𝑥_𝑖≠𝑥_𝑗\),问这些限制是否能够全部满足。
思路:并查集和离散化直接用
#include<bits/stdc++.h>
using namespace std;
const int M = 100000005;struct opt{int x, y, e;
} nn[M];int t, n;
int num[M];
int cnt[M];inline int read(){int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}int find(int x) {return x==num[x] ? x:num[x] = find(num[x]);
}bool cmp(opt a, opt b) {return a.e > b.e;
}int main() {t = read();while(t--) {int tot = 0;n = read();for (int i = 0; i < n; i++) {nn[i].x = read();nn[i].y = read();nn[i].e = read();cnt[tot++] = nn[i].x; cnt[tot++] = nn[i].y;}sort(cnt, cnt+tot);int len = unique(cnt, cnt+tot) - cnt;for (int i = 0; i < n; i++) {nn[i].x = lower_bound(cnt, cnt+len, nn[i].x) - cnt;nn[i].y = lower_bound(cnt, cnt+len, nn[i].y) - cnt;}for (int i = 0; i < len; i++) {num[i] = i;}sort(nn, nn+n, cmp);int flag = 1;for (int i = 0; i < n; i++) {int f1 = find(nn[i].x), f2 = find(nn[i].y);if (nn[i].e == 1) {if (f1 != f2) num[f1] = f2;}else {if (f1 == f2) {flag = 0;break;}}}if (flag) printf("YES\n");else printf("NO\n");}return 0;
}
并查集 – 扩展域
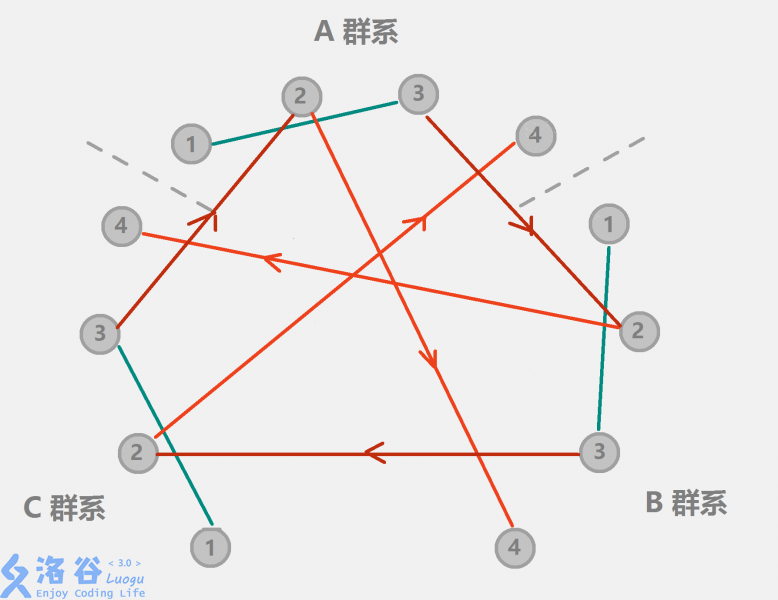
T2 食物链
问题简述:
有三种动物 \(𝐴,𝐵,𝐶\),\(𝐴\) 吃 \(𝐵\),\(𝐵\) 吃 \(𝐶\),\(𝐶\) 吃 \(𝐴\)。
现在有 \(𝑛\) 只动物,每只属于 \(𝐴,𝐵,𝐶\) 中的一种。
给出 \(𝑚\) 条限制,形如 \(𝑥,𝑦\) 品种相同,或者 \(𝑥\) 吃 \(𝑦\) 。
询问有哪些限制与前面的限制冲突(如果冲突,这条限制就失效)
思路:见图
最小生成树
定义:无向图中所有生成树中,边权和最小的。
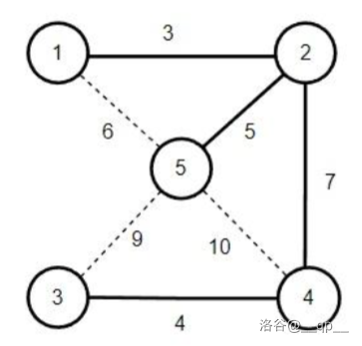
最小生成树:Kruskal
从“边权最小的边一定在最小生成树中”的想法入手,每次加入边权最小的边 \((𝑢,𝑣,𝑤)\),并把 \(𝑢\) 和 \(𝑣\) 合并为一个连通块。
也即,把所有的边按照边权排序,查看每条边是否与之前的边成环(使用并查集),若不成环则加入最小生成树。
复杂度 \(𝑂(𝑚 log𝑚 )\)。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<set>
#include<unordered_map>
#include<bitset>
#define int long long
using namespace std;
const int MAXN=100005;
struct edge {int u, v, w;
}edges[MAXN];bool compare(edge A,edge B){return A.w < B.w;
}int fa[MAXN];
int n, m;int find(int x){return fa[x]==x?x: fa[x]= find(fa[x]);
}
void merge(int u, int v){fa[find(u)]=find(v);
}
signed main(){cin >> n >> m;for(int i=0; i < m; i++){cin >>edges[i].u >> edges[i].v >> edges[i].w;}sort(edges,edges + m,compare);for(int i=0; i <n; i++){fa[i]=i;}int totWeight =0;for(int i =0; i < m; i++){if(find(edges[i].u)!= find(edges[i].v)){merge(edges[i].u, edges[i].v);totWeight + edges[i].w;}}
}
最小生成树:Prim
或者维护一个连通块,每次向外延伸一条最短边,将新的点合并进连通块内。
时间复杂度 \(𝑂(𝑛𝑚)\),使用优先队列进行优后 \(𝑂(𝑚 \log𝑛 )\)。
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int N = 1e5 + 10;
int dis[N];
int n, m;
bool vis[N];
vector<pair<int, int> >edges[N];
int main(){cin >> n >> m;for(int i = 0,u , v, w; i< m; i++){cin >> u >> v >> w;edges[u].emplace_back(v, w);edges[v].emplace_back(u, w);}vis[1]= true;int totWeight=0;for(int T = 0;T < n - 1; T++){memset(dis,0x3f,sizeof(dis));for(int i=0;i<n; i++){if(!vis[i]){continue;}for(auto edge : edges[i]){if(!vis[edge.first]){dis[edge.first] = min(dis[edge.first], edge.second);}}}int min_dis = 1 << 30, min_id = 0;for(int i = 0;i < n; i++){if(!vis[i] && dis[i] < min_dis){min_dis = dis[i], min_id = i;}totWeight += min_dis;vis[min_id]= true;}} return 0;
}
Prim 的优化
每次找出向外“延伸的最短边”可以用优先队列优化
其实这样写复杂度不是严格 \(𝑂(𝑚 \log𝑛 )\),因为队列大小可能 \(>𝑛\) (但是是 \(𝑂(𝑚 \log𝑚 )\))。使用平衡树可以变为严格 \(𝑂(𝑚 \log𝑛 )\)。
void dfs(int x,int parent,int depth){pos[x]=++time;f[0][time]=make_pair(depth,x);for(auto &y:son[x]){if(y!=parent){dfs(y,x,depth+1);f[0][++time]=make_pair(depth,x);}}
}
for(int i=2;i<=time;i++){high_bit[i]=high_bit[i>>1]+1;
}
for(int i=1;i<=high_bit[time];i++){for(int j=1;j+(1<<i)-1<=time;j++){f[i][j]=min(f[i-1][j],f[i-1][j+(1<<i-1)]);}
}
int lca(int x,int y){int L=min(pos[x],pos[y]),R=max(pos[x],pos[y]);int x=high_bit[R-L+1];return min(f[x][L],f[x][R-(1<<x)+1]).second;
}
最小生成树
如果图中某些边边权相等,则最小生成树可能不唯一。使用 Kruskal 算法或者 Prim 算法可以求出某个最小生成树。
RMQ LCA
利用 st 表可以 \(𝑂(𝑛 \log𝑛 )−𝑂(1)\) 求 LCA 。
观察欧拉序中 \(𝑥\) 走到 \(𝑦\) 的过程(假设 \(𝑥\) 欧拉序小于 \(𝑦\)),发现在这段区间内,深度最小的点就是 LCA 。
记 \(𝑓(𝑖,𝑗)\) 为欧拉序中 \([𝑖,𝑖+2^𝑗−1]\) 的最浅深度,\(𝑔(𝑖,𝑗)\) 为其编号。
dfs 预处理。
\((𝑓,𝑔)\) 记为一个 \(pair<int, int>\) 更方便。
const int MAXX = 1e5 + 10, MAXN = 1e9 + 10;
inline int read(){int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}
int f[MAXN][MAXN];
int fa[MAXN];
int dep[MAXN];
int lca(int x,int y){if(dep[x]>dep[y])swap(x,y);for(int j=20;j>=0; j--)if(dep[f[y][j]]>= dep[x])y=f[y][j];if(x == y)return x;for(int j=20;j>=0; j--){if(f[x][j]!= f[y][j]){x=f[x][j];y=f[y][j];}}return f[x][0]; //f[x][e] == f[y][e]
}signed main(){f[i][0] = fa[i];for(int j = 1;j <= 20;j++){for(int i = 1;i <= n;i++){f[i][j] = f[f[i][j - 1]][j - 1];}}return 0;
}
最短路径问题
单源最短路:给定起点 \(𝑠\),求出 \(𝑠\) 到其它所有点的最短路。
边权任意(Bellman−Ford,SPFA) / 边权非负(Dijkstra)。
多源最短路:求出所有点对之间的最短路。边权任意
(Floyd)。
多源最短路:Floyd
设 \(𝑓(𝑘,𝑖,𝑗)\) 为,在仅考虑编号 \(≤𝑘\) 的节点时,\(𝑖→𝑗\) 的最短距离(路径上除了 \(𝑖,𝑗\) 外节点编号都 \(≤𝑘\))。
复杂度 \(𝑂(𝑛^3 )\)。
#include <bits/stdc++.h>
using namespace std;
int n,m,dis[...][...];
int main(){cin >> n >> m;memset(dis,0x3f,sizeof(dis));for(int i=0,u,v,w;i<m;i++){cin >> u >> v >> w;dis[u][v]=min(dis[u][v],w);}for(int k=0;k<n;k++)for(int i=0;i<n;i++)for(int j=0;j<n;j++)dis[i][j]=min(dis[i][j],dis[i][j]+dis[k][j]);return 0;
}
以 \(𝑖,𝑗,𝑘\) 顺序枚举错误的例子:
由于是按照 \(𝑖,𝑗,𝑘\) 顺序枚举的,则 \(𝑑𝑖𝑠[0][1]\) 只会在第4一轮更新。但此时 \(𝑑𝑖𝑠[2][1]\) 和 \(𝑑𝑖𝑠[0][3]\) 都是 \(INF\) ,导致无法更新到 \(𝑑𝑖𝑠[0][1]\)。
/*wrong*/
#include <bits/stdc++.h>
using namespace std;
int n,m,dis[...][...];
int main(){cin >> n >> m;memset(dis,0x3f,sizeof(dis));for(int i=0,u,v,w;i<m;i++){cin >> u >> v >> w;dis[u][v]=min(dis[u][v],w);}for(int i=0;k<n;k++)for(int j=0;i<n;i++)for(int k=0;j<n;j++)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);return 0;
}
单源最短路:Bellman−Ford
当图中存在负环时,可以先从 \(𝑠\) 走到负环,然后无限绕圈,则 \(𝑠→𝑖\) 的路径可以无限小。
此时表现为一直有某些个 \(𝑑𝑖𝑠\) 被成功更新。因为如果不存在负环,那么 \(𝑠→𝑖\) 的最短路边数一定 \(≤𝑛−1\),则更新完 \(𝑛−1\) 轮后,\(𝑑𝑖𝑠\) 不再变化。
所以可以额外检查是否一直有 \(𝑑𝑖𝑠\) 被更新 ,以此来判断图中是否有负环。
#include <bits/stdc++.h>
using namespace std;
struct edge{int u,v,w;
}edges[...];
int n,m,s,dis[...];
int main(){cin >> n >> m >> s;memset(dis,0x3f,sizeof(dis));for(int i=0,u,v,w;i<m;i++)cin >> edges[i].u >> edges[i].v >> edges[i].w;dis[s]=0;for(int T=0;T<n;T++)for(int i=0;i<m;i++)dis[edges[i].v]=min(dis[edges[i].v],dis[edges[i].u]+edges[i].w);return 0;
}
单源最短路:SPFA
SPFA 算法是队列优化的 Bellman−Ford 算法。
一开始将 \(𝑠\) 置入队列,每次取出队头,并将有效松弛后的点重新置入队列,表示可以用这个点更新其它点。
由于无负环时,每个点最多入队 \(𝑛−1\) 次,则复杂度 \(𝑂(𝑛𝑚)\)。在不被特意卡的随机情况下复杂度约为 \(𝑂(𝑘𝑚)\) ,\(𝑘\) 为某常数。
不要使用 SLF, LLL 等“优化”,会被卡到指数级。
#include <bits/stdc++.h>
using namespace std;
int n,m,s,dis[...];
bool inqueue[...];
queue<int> Q;
vector<pair<int,int> > edges[...];
int main(){cin >> n >> m >> s;memset(dis,0x3f,sizeof(dis));for(int i=0,u,v,w;i<m;i++){cin >> u >> v >> w;edges[u].emplace_back(v,w);}dis[s]=0;Q.push(s);inqueue[s]=true;while(!Q.empty()){int x=Q.front();Q.pop();inqueue[x]=false;for(auto edge:edges[x]){if(dis[edge.first]<=dis[x]+edge.second)continue;dis[edge.first]=dis[x]+edge.second;if(!inqueue[edge.first]){Q.push(edge.first);inqueue[edge.first]=true;}}}return 0;
}
如果某个节点入队次数 \(≥𝑛\),则表示其被成功松弛 \(≥𝑛\) 次。
与 Bellman−Ford 类似,此时说明图中存在负环。
所以可以额外记录每个节点的入队次数。
或者可以记录每个节点的最短路边数 \(𝑐𝑛𝑡[𝑖]\),当用 \(𝑢\) 更新 \(𝑣\) 时,令 \(𝑐𝑛𝑡[𝑣]=𝑐𝑛𝑡[𝑢]+1\)。如果 \(𝑐𝑛𝑡[𝑖]≥𝑛\) ,则存在负环。
单源最短路:Dijkstra
在边权非负的情况下,可以使用 Dijkstra 算法。
类似于 Prim 算法,维护一个已经考虑完毕点的集合,每次向外拓展最短距离的点。
使用优先队列优化,复杂度为 \(𝑂((𝑛+𝑚) \log𝑛 )\)。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
int n,m,s,dis[...];
bool vis[...];
vector<pii> edges[...];
priority_queue<pii,vector<pii>,greater<pii> > Q;
int main(){cin >> n >> m >> s;for(int i=0,u,v,w;i<m;i++){cin >> u >> v >> w;edges[u].emplace_back(v,w);}Q.push({0,s});memset(dis,0x3f,sizeof(dis));dis[s]=0;while(!Q.empty()){pii info=Q.top();Q.pop();int x=info.second;if(dis[x]!=info.first)continue;for(auto e:edges[x]){if(dis[e.first]<=dis[x]+e.second)continue;dis[e.first]=dis[x]+e.second;Q.push({dis[e.first],edge.first});}}return 0;
}
Dijkstra 是一个贪心算法。与 SPFA 算法不同的是,ijkstra 过程中每个节点只会入队一次。
其正确性建立在边权非负的基础上。假设 \(1\) 号点到 \(5\) 号点的最短路径具体为 \(1→2→4→5\),由于 \(4→5\) 这条边权非负,那么在加入 \(5\) 号点之前,\(4\) 号点一定被加入过了。从而最短路径一定会被考虑到。
如果边权可以为负,则不能使用 Dijkstra 算法。
一个反例:
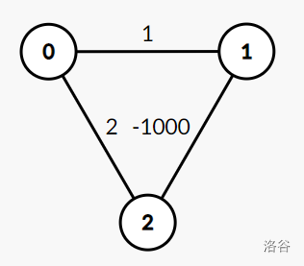
在这个反例中,会首先从 \(0\) 号点拓展 \(1\) 号点,错误。
单源最短路:01−BFS
当边权仅为 $0/1¥ 时,可以使用 01−BFS 算法计算单元最短路。
维护双端队列,遇到 \(0\) 边时将下一个点加到队头,遇到 \(1\) 边时将下一个点加到队尾。
这样在 BFS 到某个点时,会先访问所有与其距离为 \(0\) 的点。
相当于先把所有 \(0\) 边缩起来,再跑一般的 BFS 。
复杂度 \(𝑂(𝑛+𝑚)\)。
(右图中的写法可能一个点入队多次,不过由于 \(𝑑𝑖𝑠\) 小的情况一定在前,所以不影响复杂度)