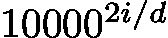- Rank&挂分
- A. BA
- 题目内容
- 部分分
- 10pts
- 10+20pts
- 正解
- 思路
- 代码
- B. BB
- 题目内容
- 部分分
- 5pts
- 正解
- 思路
- 代码
- C. BC
- D. BD
Rank&挂分

T4暴搜后来改了记搜,不知道哪里锅了,挂5pts。
A. BA
题目内容
现在有 \(m\) 块烙板,\(n\) 张饼,第 \(i\) 张饼需要烙 \(a_i\) 个单位时间,一张饼一个单位时刻只能在一张烙板上,问都烙熟所需最少时间。
部分分
10pts
暴力深搜,每次枚举在锅里放什么饼,然后在所有合法方案里找最优解。
10+20pts
对Subtask 2进行特判,由于饼只有一面或两面,所以优先处理两面一定更优,配合前面的10分,可以拿下30分。
正解
思路
首先由于一张饼在同一时间只能出现在一口锅里的限制(以下简称时间冲突),可知答案的下界是所有 \(a_i\) 的 \(max\)。
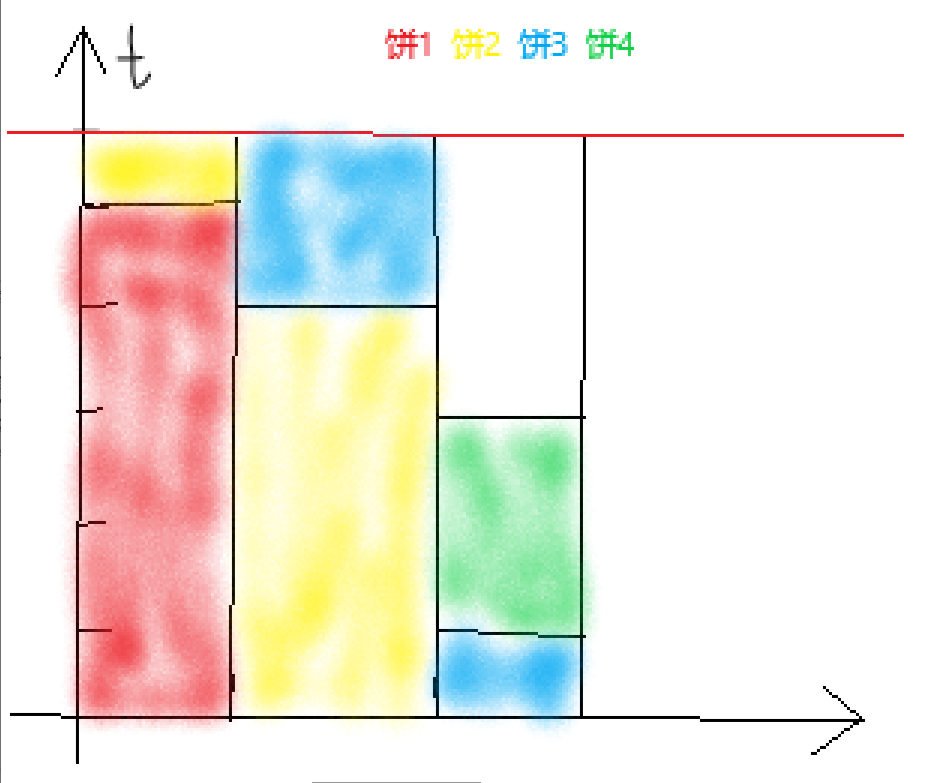
从上图可以看出,如果耗时最长的饼都不会发生时间冲突,则一定存在一种方案使得没有饼会产生时间冲突。不考虑时间冲突的因素,那么只要保证 \(m\times t\ge\sum\limits^{n}_{i=1}a_i\) 即可。这里的处理既可以二分,也可以直接求。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b;
long long sm,ans,mx,c;
int main()
{scanf("%d%d",&a,&b);for(ri i=1;i<=a;i++){scanf("%lld",&c);mx=max(mx,c);sm+=c;}ans=sm/b;if(sm%b){ans++;}ans=max(ans,mx);printf("%lld",ans);return 0;
}
B. BB
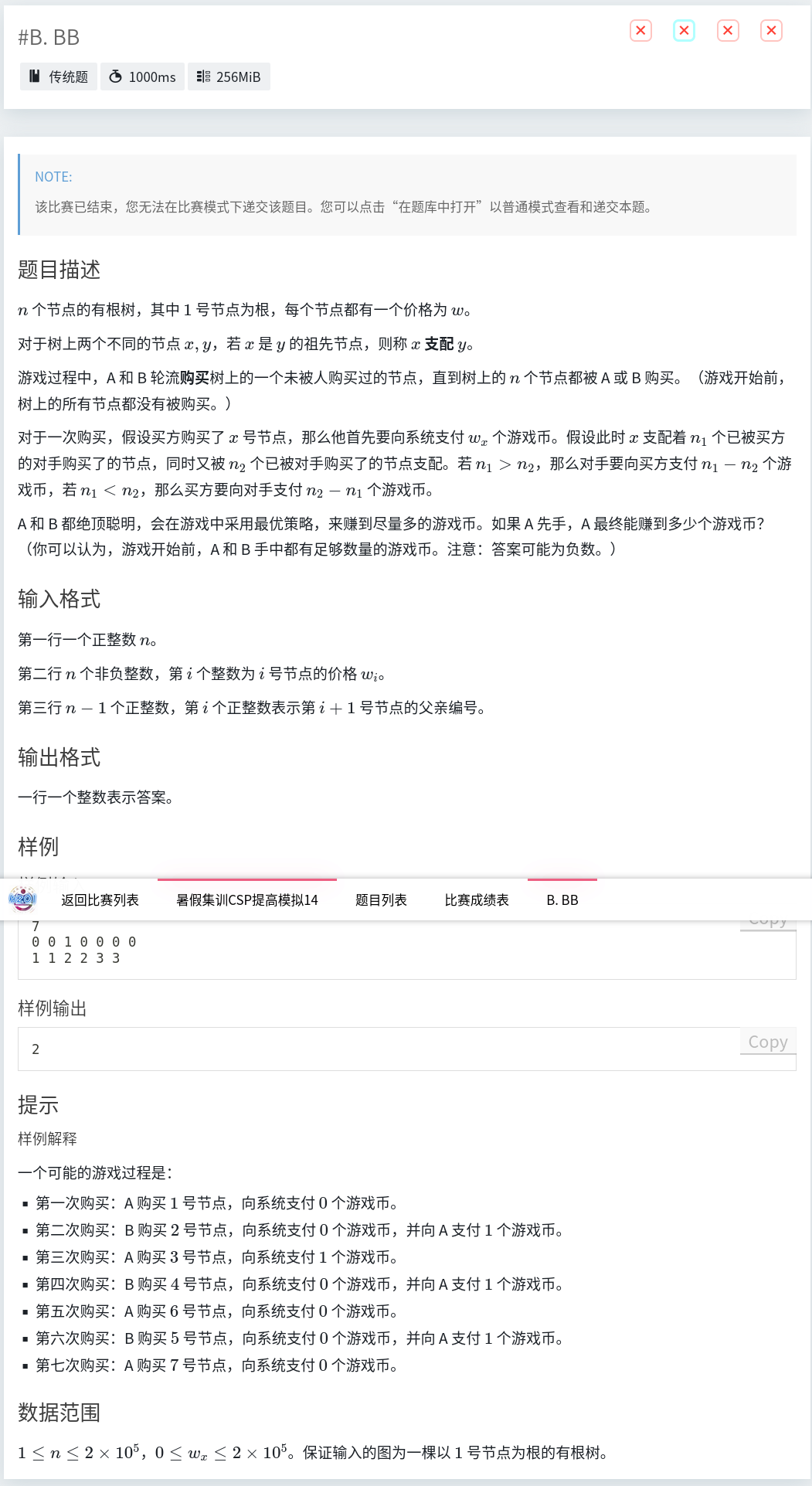
题目内容
洛谷原题
\(n\) 个节点的有根树,其中 \(1\) 号节点为根,每个节点都有一个价格为 \(w\)。
对于树上两个不同的节点 \(x,y\),若 \(x\) 是 \(y\) 的祖先节点,则称 \(x\) 支配 \(y\)。
游戏过程中,A 和 B 轮流购买树上的一个未被人购买过的节点,直到树上的 \(n\) 个节点都被 A 或 B 购买。(游戏开始前,树上的所有节点都没有被购买。)
对于一次购买,假设买方购买了 \(x\) 号节点,那么他首先要向系统支付 \(w_x\) 个游戏币。假设此时 \(x\) 支配着 \(n_1\) 个已被买方的对手购买了的节点,同时又被 \(n_2\) 个已被对手购买了的节点支配。若 \(n_1\gt n_2\),那么对手要向买方支付 \(n_1-n_2\) 个游戏币,若 \(n_1\lt n_2\),那么买方要向对手支付 \(n_2-n_1\) 个游戏币。
A 和 B 都绝顶聪明,会在游戏中采用最优策略,来赚到尽量多的游戏币。如果 A 先手,A 最终能赚到多少个游戏币?(你可以认为,游戏开始前,A 和 B 手中都有足够数量的游戏币。注意:答案可能为负数。)
部分分
5pts
树剖,不知道哪里锅了,WA,但是没TLE。
正解
思路
设 A 选择的点的点集为 U,B 选择的点的点集为 V。考虑一个点 \(n\) 对 A 的收益的贡献:如果 n 祖先有 \(p\) 个属于 V 的点,则选 \(n\) 会使 A 的收益减少 \(p\);如果 n 儿子有 \(q\) 个属于 V 的点,则选 \(n\) 会使 A 的收益增加 \(q\);总收益就是 \(q-p\)。关于这个可以对在选 \(n\) 前和选 \(n\) 后进行分讨来理解。
但是仅仅转化到此还是不好维护,我们从点集里所有的点的角度去考虑:
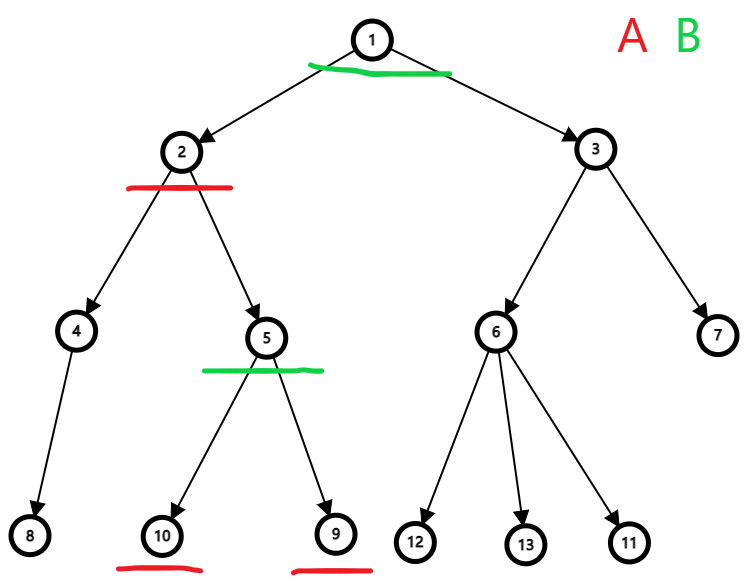
如果我们直接把祖先数和儿子数作为贡献,显然,同色的在计算时多计算的一部分会相互抵消。这个还是感性理解吧。
于是,一个点的权值被转化为儿子数减祖先数再减它本身的权值。儿子数可以类比树剖的 \(siz_x-1\) 计算,祖先数就是深度 \(dep_x-1\),两个 \(-1\) 抵消,最终的式子是 \(siz_x-dep_x-w_x\),然后贪心即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b[200002],fa[200002],f[200002],g,dep[200002],siz[200002];
priority_queue<int>que;
long long ans;
struct node
{int h,to;
}pic[200002];
il void ndin(int x,int y)
{g++;pic[g].to=y;pic[g].h=f[x];f[x]=g;
}
void dfs(int x)
{siz[x]=1;dep[x]=dep[fa[x]]+1;for(ri i=f[x];i;i=pic[i].h){ri y=pic[i].to;if(y!=fa[x]){dfs(y);siz[x]+=siz[y];}}
}
int main()
{scanf("%d",&a);for(ri i=1;i<=a;i++){scanf("%d",&b[i]);}for(ri i=2;i<=a;i++){scanf("%d",&fa[i]);ndin(fa[i],i);}dfs(1);for(ri i=1;i<=a;i++){que.push(siz[i]-dep[i]-b[i]);}while(que.size()>1){ans+=que.top();que.pop();que.pop();}if(que.size()){ans+=que.top();que.pop();}printf("%lld",ans);return 0;
}
C. BC
->to be continue.
D. BD
->to be contniue.