1.九次九日九重色

一开始做的时候被题面给迷惑住了,没想到可以跳着 匹配(样例太水)。
那我们来考虑如何做,首先思路肯定是把能匹配的暴力求出来,根据不知道怎么搞的调和计数,这样的复杂度还不是很高,是\(O(NlogN)\),可以搞。
观察一下预处理出来的序列,是不是很熟悉。没错剩下的就是求最长上升子序列。
那求最长上升子序列有两种方法,一个是\(O(n^2)\)的DP,还有一个\(O(NlogN)\)的二分。
这里主要了解后面的(因为赛时我还不会)。
原理其实比较简单,看代码就能看懂。
点击查看代码
#include<bits/stdc++.h>
using namespace std;const int N=2e5+107;int n;
struct lmy
{int x,y;
}a[N];
bool comp(lmy a,lmy b)
{return a.x<b.x;
}
int s[N],tp;int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d%d",&a[i].x,&a[i].y);}sort(a+1,a+1+n,comp);for(int i=1;i<=n;i++){if(s[tp]<a[i].y) s[++tp]=a[i].y;else{s[lower_bound(s+1,s+1+tp,a[i].y)-s]=a[i].y;}}printf("%d",tp);
}
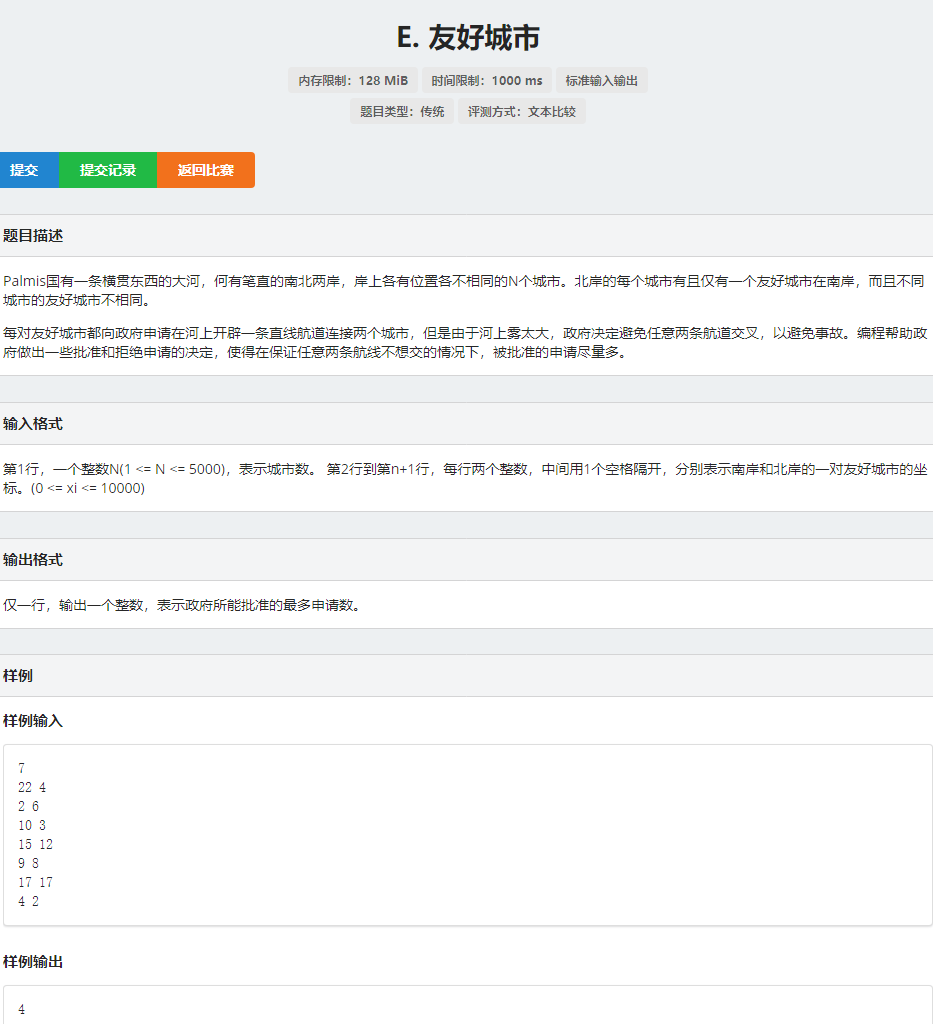
2.天色天歌天籁音
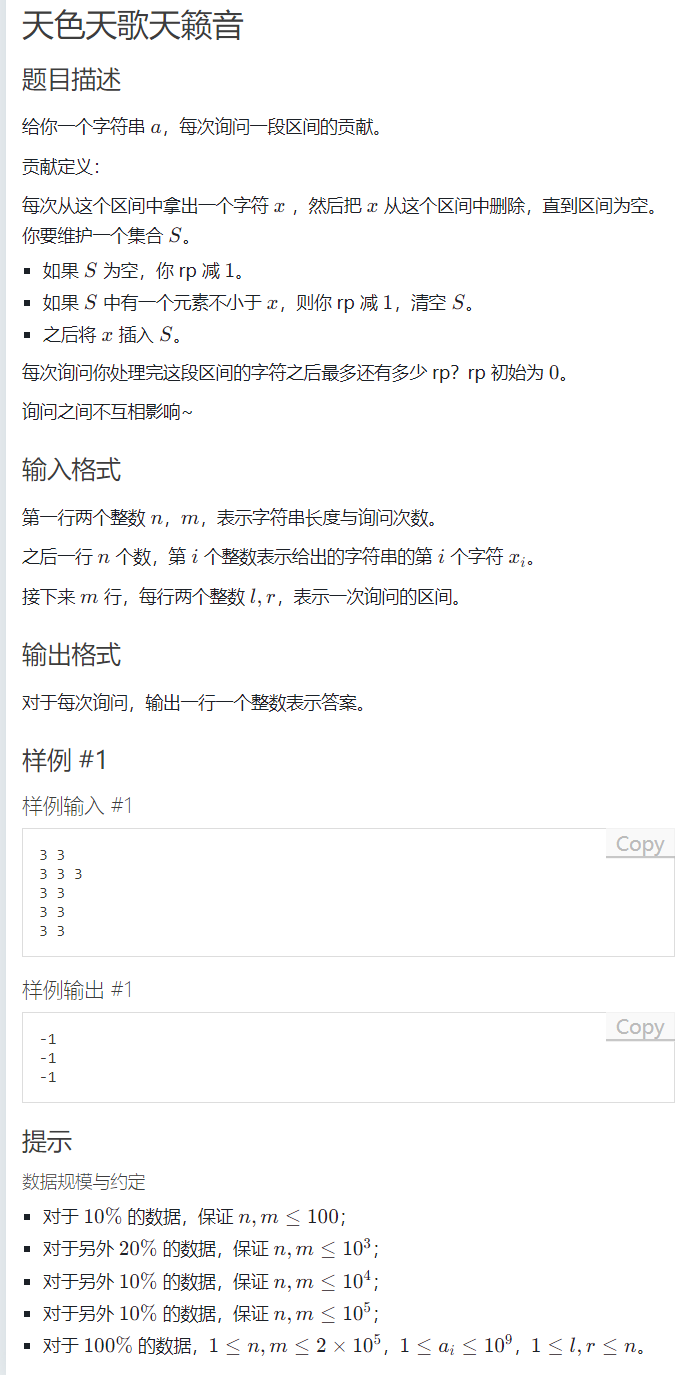
简单理解一下题意,再自己手模一下,可以发现题目所求的是区间众数,然后它强调了一下各个互不影响,可以考虑莫队(其实挺套路的,但我不会莫队了,大悲)。
主要讲讲add和del的操作,
首先add比较好说,只需要直接计数。
del就需要分讨一下。
1.减之前比目前最大众数小,无影响。
2.本身是最大众数,减完之后还是,无影响。
3.本身为最大众数(但众数有很多个),减之后不为最大众数(主要的问题)。
关于这个问题,我们就可以开一个桶来记录每个数出现个数(众数)的个数(是有点绕,得理解一下),到这这个题就没什么了
点击查看代码
#include<bits/stdc++.h>
using namespace std;const int N=3e5+107;
int n,m,a[N];int li[N],ri[N],bg[N],tot;
struct lmy
{int x,y,id;
}q[N];
bool comp(lmy &a,lmy &b)
{int p=bg[a.x],q=bg[b.x];if(p!=q) return p<q;if(p&1) return a.y<b.y;else return a.y>b.y;
}void fk()
{int sq=sqrt(n);for(int i=1;i<=sq;i++){li[i]=ri[i-1]+1;ri[i]=sq*i;if(i==sq) ri[i]=n;for(int j=li[i];j<=ri[i];j++) bg[j]=i;}
}map<int,int> mp;int sum,t[N],cnt[N],ans[N];
void add(int i)
{t[cnt[a[i]]]--;t[++cnt[a[i]]]++;sum=max(sum,cnt[a[i]]);
}void del(int i)
{t[cnt[a[i]]]--;if(cnt[a[i]]==sum&&!t[cnt[a[i]]]) sum--;t[--cnt[a[i]]]++;
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) {scanf("%d",&a[i]);if(mp.find(a[i])==mp.end()){mp[a[i]]=++tot;}a[i]=mp[a[i]];}fk();for(int i=1;i<=m;i++){int l,r;scanf("%d%d",&l,&r);q[i]={l,r,i};}sort(q+1,q+1+m,comp);int l=1,r=0;for(int i=1;i<=m;i++){while(r<q[i].y) add(++r);while(r>q[i].y) del(r--);while(l<q[i].x) del(l++);while(l>q[i].x) add(--l);ans[q[i].id]=sum;}for(int i=1;i<=m;i++) printf("%d\n",-ans[i]);
}