双倍经验:Luogu P5089 元素周期表 ,CF1012B Chemical table:模拟赛搬的好题,有点厉害。赛时10min码的假贪心拿了五十多分,赢。
并查集思路 1
对于此类棋盘整行整列覆盖问题,有一个通用思路:把每一行和每一列看作一个点,那么原本棋盘上的格子就可以看作是连接这些点的边。例如一个点是 \((x,y)\) ,那么我们就可以把行 \(x\) 代表的点与列 \(y\) 代表的点连一条边。
这样做的原因是如果确定了行与列,那么我们就可以确定唯一的点。并且本题还是整行整列地进行覆盖的,数据范围较大,只能通过此类表达方式来把原来 \(10^{12}\) 级别的点,化为 \(10^{12}\) 级别的边;剩下点的个数就为 \(2 \times 10^6\) 级别。
一些这种图的性质:
- 如果第 \(i\) 行与第 \(j\) 列联通,可以当成格子 \((i,j)\) 处有一个点。
- 本质上是把每个已有的格子,从横纵两个方向散开直线,这些直线只要形成交点,就是一个连通块。在本题中这么应用,是因为只要有 \(3\) 个点,我们就可以确定一个矩形。
接下来思考核聚变的过程:
对于点 \((x_1,y_1),(x_1,y_2),(x_2,y_1),(x_2,y_2)\) 组成一个矩形 ,我们先假设 \((x_2,y_2)\) 还没有生成。
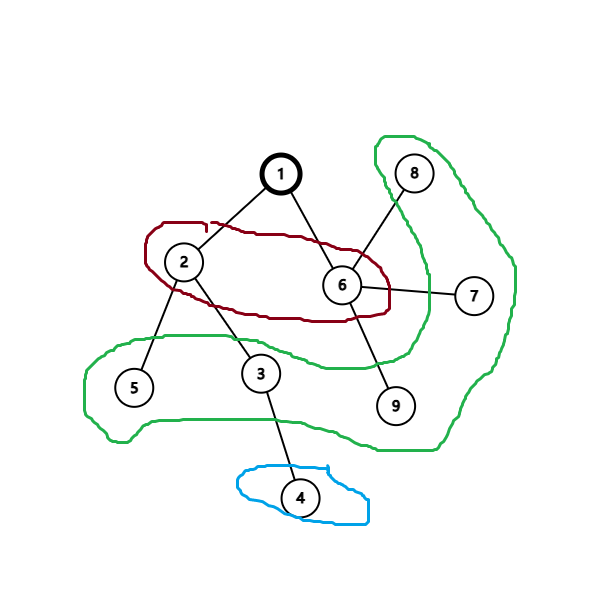
那么连出的图就长这样:(圆表示 \(x\) ,方表示 \(y\) 。)

可以发现,点 \(x_2\) 与点 \(y_2\) 已经是联通的了,并且由于上述的第一条性质:如果第 \(i\) 行与第 \(j\) 列联通,可以当成格子 \((i,j)\) 处有一个点。此时的点已经自动被拓展了出来。
于是,我们只需要把 \(n+m\) 个所有的点都合并成一个连通块,就可以了。
这个过程可以用并查集维护。
合并的次数就是连通块的个数 \(-1\) 。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,q,f[2000005],ans=0;
void init()
{for(int i=1;i<=n+m;i++)f[i]=i;
}
int findf(int x)
{if(f[x]!=x)f[x]=findf(f[x]);return f[x];
}
void combine(int x,int y)
{int fx=findf(x),fy=findf(y);f[fx]=fy;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>q;init();while(q--){int x,y;cin>>x>>y;combine(x,y+n);}for(int i=1;i<=n+m;i++){ans+=(findf(i)==i);}cout<<ans-1;return 0;
}
并查集思路 2
某位金钩爷的做法,有点复杂,但也好理解。这种做法是单纯从本题的生成点的性质入手,而上一种做法就是单纯从套路上入手。
首先我们画个图:

可以发现,如果相邻两行的同一列有棋子(蓝色部分),那么这两行就完全同步状态了。例如我们往第一行加上一些绿色点,那么我们下面的紫色部分也会加上一些点。他们的状态是完全同步的。
进一步拓展结论,就可以得到如果任意两行的同一列有棋子,那么这两行就同步状态了,所以他们就成连通块了。
最终我们拓展完后,一定会形成一些没有相同列的连通块。
于是我们一开始就把行看成点,对有相同列的进行合并,统计连通块个数(空行不能和空行算一个连通块)。
然后特判一下有没有空列,答案就是连通块个数 \(-1\) 加上空列个数。
比上一种好理解一点。代码就不写了,我懒。
二分图思路
和并查集思路 1 的做法差不多,把二分图分成上面行一部分,下面列一部分,然后照常合并。
然后遇到不连通的部分合并一下,统计一下就好了。基本和并查集一样。
代码就不写了,我懒。*2