探究grid_sample函数

一、函数介绍

torch.nn.functional.grid_sample(input, grid, mode='bilinear', padding_mode='zeros', align_corners=None)

• 对于4D输入，input维度为 \((N,C,H_{in},W_{in})\), grid维度为 \((N,H_{out},W_{out},2)\) ，则output维度为 \((N,C,H_{out},W_{out})\)

• 对于5D输入，input维度为 \((N,C,D_{in},H_{in},W_{in})\), grid维度为 \((N,D_{out},H_{out},W_{out},3)\) ，则output维度为 \((N,C,D_{out},H_{out},W_{out})\)

• gird储存着用于在输入特征图上进行元素采样的坐标偏移量。grid的元素值通常在 \(\left [-1, 1 \right ]\) 之间， \(\left (-1, -1 \right )\) 表示取输入特征图左上角的元素， \(\left (1, 1 \right )\) 表示取输入特征图右下角的元素。

二、示例代码

import torch
import torch.nn.functional as F# 定义一个 4x4 的输入张量
input_tensor = torch.tensor([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12],[13, 14, 15, 16],
], dtype=torch.float).view(1, 1, 4, 4)# 定义采样点，归一化坐标在 [-1, 1] 范围内
# 这里使用小数坐标进行采样
grid = torch.tensor([[[[-0.5, -0.5], [0.5, -0.5]],[[-0.5, 0.5], [0.5, 0.5]]]], dtype=torch.float)# 使用 F.grid_sample 进行采样
output = F.grid_sample(input_tensor, grid, align_corners=True)print(output)

补充知识：

1.性插值法（linear interpolation）

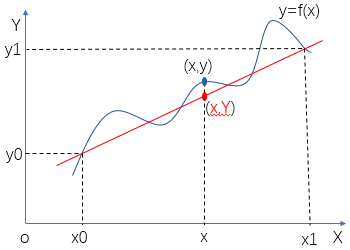
假设我们已知坐标 ((x0, y0) 与 (x1, y1)，要得到 [x0, x1] 区间内某一位置 x 在直线上的值。根据图中所示，我们得到

\[\frac{y-y_0}{x-x_0} = \frac{y_1 - y_0}{x_1 - x_0} \]

由于 x 值已知，所以可以从公式得到 y 的值

\[y=y_{0}+\left(x-x_{0}\right) \frac{y_{1}-y_{0}}{x_{1}-x_{0}}=y_{0}+\frac{\left(x-x_{0}\right) y_{1}-\left(x-x_{0}\right) y_{0}}{x_{1}-x_{0}} \]

2.双线性插值法（bilinear interpolation）

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

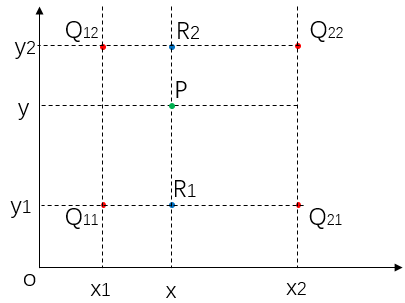
如坐标图所示，用横纵坐标代表图像像素的位置，f(x,y)代表该像素点(x,y)的彩色值或灰度值。

假设我们已知函数f(x,y)在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值

若想得到未知函数f(x,y)在点P=(x, y)的值，首先在 x 方向进行线性插值，得到

\[f(x,y_{1})\approx\frac{x_{2}-x}{x_{2}-x_{1}}f(Q_{11})+\frac{x-x_{1}}{x_{2}-x_{1}}f(Q_{21}),\\f(x,y_{2})\approx\frac{x_{2}-x}{x_{2}-x_{1}}f(Q_{12})+\frac{x-x_{1}}{x_{2}-x_{1}}f(Q_{22}). \]

然后在 y 方向进行线性插值，得到

\[f(P)\approx\frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2). \]

这样就得到所要的结果 f(x, y)，

\[\begin{aligned} f(x,y) \approx\frac{y_{2}-y}{y_{2}-y_{1}}f(x,y_{1})+\frac{y-y_{1}}{y_{2}-y_{1}}f(x,y_{2}) \\ =\frac{1}{(x_{2}-x_{1})(y_{2}-y_{1})}[ x_{2}-x\quad x-x_{1} ]{\begin{bmatrix}f(Q_{11})&f(Q_{12})\\f(Q_{21})&f(Q_{22})\end{bmatrix}}{\begin{bmatrix}y_{2}-y\\y-y_{1}\end{bmatrix}}. \end{aligned} \]

2.1 单位正方形
如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

\[f(x,y)\approx f(0,0)\left(1-x\right)(1-y)+f(1,0)x(1-y)+f(0,1)\left(1-x\right)y+f(1,1)xy. \]

或者用矩阵运算表示为

\[f(x,y)\approx[\begin{matrix}{1-x}&{x}\\\end{matrix}]\biggl[\begin{matrix}{f(0,0)}&{f(0,1)}\\{f(1,0)}&{f(1,1)}\\\end{matrix}\biggr]\biggl[\begin{matrix}{1-y}\\{y}\\\end{matrix}\biggr] \]

2.2 非线性
双线性插值的结果不是线性的，它是两个线性函数的积。在单位正方形上，双线性插值可以记作

\[f(x,y)=\sum_{i=0}^1\sum_{j=0}^1a_{ij}x^iy^j=a_{00}+a_{10}x+a_{01}y+a_{11}xy \]

常数的数目（4个）对应于给定的 f 的数据点数目

\[\begin{aligned} &a_{00} =f(0,0), \\ &a_{10} =f(1,0)-f(0,0), \\ &a_{01} =f(0,1)-f(0,0), \\ &a_{11} =f(1,1)+f(0,0)-\big(f(1,0)+f(0,1)\big). \end{aligned}\]

双线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。双线性插值的一个显然的三维空间延伸是三线性插值。

参考文章：

1. 一文彻底弄懂 PyTorch 的 F.grid_sample
2. PyTorch中grid_sample的使用方法
3. 通俗易懂】详解torch.nn.functional.grid_sample函数：可实现对特征图的水平/垂直翻转
4. 双线性插值（Bilinear Interpolation） 原理、存在的问题及其解决方案、OpenCV代码实现