- P1981 [NOIP2013 普及组] 表达式求值
- P1449 后缀表达式
- P5788 【模板】单调栈
- P1886 滑动窗口 /【模板】单调队列
- P1901 发射站
- P1540 [NOIP2010 提高组] 机器翻译
- P2085 最小函数值
- P6033 [NOIP2004 提高组] 合并果子 加强版
- P1631 序列合并
- P2251 质量检测
- P1305 新二叉树
- B3631 单向链表
- P1739 表达式括号匹配
- P1996 约瑟夫问题
- P1808 单词分类
- B3616 【模板】队列
- P3378 【模板】堆
- P4715 【深基16.例1】淘汰赛
P1981 [NOIP2013 普及组] 表达式求值
- P1981 [NOIP2013 普及组] 表达式求值
给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。
输入一行需要计算的表达式,表达式中只包含数字、加法运算符‘+’和乘法运算符‘×’,且没有括号,所有参与运算的数字均为 0 到 pow(2,31)-1之间的整数。输入数据保证这一行只有 0-9、+、× 这12种字符。
输出一个整数,表示这个表达式的值,当答案长度多于4位时,请只输出最后4位,前导0不输出。
输入样例:1+1*3+4
输出样例:8
【分析】模拟/栈
先观察输入数据的格式,一定是:a+b+b+b...
那么可以考虑先读入 a,后面死循环读入 +b,这样就可以轻松完成数据分割。
由于有 *+,可以将 * 先处理了,后面对于 + 直接累加即可。
构建一个数字栈,遍历字符串,数字直接入栈;如果是运算符,将当前栈顶元素 a 与 b进行计算,同时pop,计算的结果push。
最后累加栈内全部元素即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
stack<long long> sta;
int a,b,ans=0, mod=10000; char ch;
int main() {cin>>a; a %= mod; sta.push(a);while(cin>>ch>>b) {b %= mod;if(ch=='*') {a = sta.top(); sta.pop();sta.push(a*b%mod);} else if(ch=='+') { sta.push(b); }}while(!sta.empty()) {ans += sta.top(), sta.pop();ans %= mod;}cout<<ans%mod; return 0;
}
P1449 后缀表达式
- P1449 后缀表达式
所谓后缀表达式是指这样的一个表达式:式中不再引用括号,运算符号放在两个运算对象之后,所有计算按运算符号出现的顺序,严格地由左而右新进行(不用考虑运算符的优先级)。
如:3*(5–2)+7 对应的后缀表达式为:3.5.2.-*7.+@。
'@'为表达式的结束符号,'.'为操作数的结束符号。字符串长度在1000内。
输入格式:后缀表达式
输出格式:表达式的值
输入样例:3.5.2.-*7.+@
输出样例:16
【分析】模拟/栈
先观察输入数据的格式,一定是:a.a.+@
每个数字后面有一个 .,可以据此进行数据分割。
构建一个数字栈,遍历字符串,数字直接入栈;
如果是运算符,将顺序取出两个栈顶元素 a,b 进行计算,计算的结果push。
最后栈顶元素就是答案。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
stack<int> sta; int a,b,c; char ch;
int main(){while((ch=getchar())!='@'){if(ch<='9' && ch>='0'){a=a*10+ch-'0';}else if(ch=='.'){sta.push(a); a=0;}else {a=sta.top(),sta.pop();b=sta.top(),sta.pop();if(ch=='+'){ c = b+a; }else if(ch=='-'){ c = b-a; }else if(ch=='*'){ c = b*a; }else if(ch=='/'){ c = b/a; }sta.push(c); a=b=0;}}cout<<c<<endl; return 0;
}
P5788 【模板】单调栈
- P5788 【模板】单调栈
给出项数为 \(n\) 的整数数列 \(a_{1 \dots n}\)。
定义函数 \(f(i)\) 代表数列中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标,即 \(f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}\)。若不存在,则 \(f(i)=0\)。
试求出 \(f(1\dots n)\)。
输入格式:第一行一个正整数 \(n\)。第二行 \(n\) 个正整数 \(a_{1\dots n}\)。
输出格式:一行 \(n\) 个整数 \(f(1\dots n)\) 的值。
| 输入样例 | 输出样例 |
|---|---|
5 1 4 2 3 5 |
2 5 4 5 0 |
【数据范围】对于 \(100\%\) 的数据,\(1 \le n\leq 3\times 10^6\),\(1\leq a_i\leq 10^9\)。
【分析】
- 求每个元素右边第一个大于该元素的值的下标。
- 维护一个单调栈,可以画一下下面这个图。

上图是从左向右遍历的单调递减栈
也可以维护一个从右向左遍历的单调递增栈。
#include<bits/stdc++.h>
using namespace std;
const int N=3e6+10;
typedef long long LL;
int n,a[N],ans[N];
int st[N],h=0;int main(){scanf("%d", &n);for(int i=1; i<=n; i++) scanf("%d", &a[i]);// 从左向右 : 维护一个单减栈for(int i=1; i<=n; i++){while(h && a[st[h]] < a[i] ){ans[st[h]] = i;h--;}st[++h] = i;}/* // 从右向左 : 维护一个单增栈 for(int i=n; i>=1; i--){while(h && a[st[h]] <= a[i]) h--;ans[i] = st[h];st[++h] = i;} */for(int i=1; i<=n; i++) printf("%d ", ans[i]);return 0;
}
P1886 滑动窗口 /【模板】单调队列
- P1886 滑动窗口 /【模板】单调队列
有一个长为 \(n\) 的序列 \(a\),以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:The array is \([1,3,-1,-3,5,3,6,7]\), and \(k = 3\)。
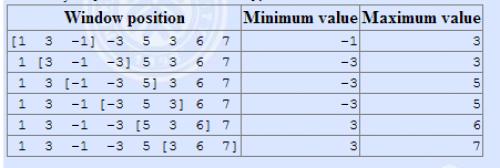
输入格式: 输入一共有两行,第一行有两个正整数 \(n,k\)。第二行 \(n\) 个整数,表示序列 \(a\)
输出格式:输出共两行,第一行为每次窗口滑动的最小值;第二行为每次窗口滑动的最大值
| 输入样例 | 输出样例 |
|---|---|
8 3 1 3 -1 -3 5 3 6 7 |
-1 -3 -3 -3 3 3 3 3 5 5 6 7 |
【数据范围】\(1\le k \le n \le 10^6\),\(a_i \in [-2^{31},2^{31})\)。
【分析】考虑两个问题
- 如何确定窗口大小:可以通过下标求差完成
- 如何确定窗口内的最值:可以利用单调队列完成
这里为了便于理解,我们画一个样例图

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N], q[N], fr=0, ta=-1;int main(){int n,m; cin>>n>>m;for(int i=1; i<=n; i++) cin>>a[i];for(int i=1; i<=n; i++){while(fr<=ta && i-q[fr]+1 > m) ++fr;while(fr<=ta && a[q[ta]]>=a[i]) --ta;q[++ta]=i;if(i>=m) cout<<a[q[fr]]<<" ";}cout<<endl;fr=0, ta=-1;for(int i=1; i<=n; i++){while(fr<=ta && i-q[fr]+1 > m) ++fr;while(fr<=ta && a[q[ta]]<=a[i]) --ta;q[++ta]=i;if(i>=m) cout<<a[q[fr]]<<" ";}return 0;
}
P1901 发射站
- P1901 发射站
某地有 \(N\) 个能量发射站排成一行,每个发射站 \(i\) 都有不相同的高度 \(H_i\),并能向两边(两端的发射站只能向一边)同时发射能量值为 \(V_i\) 的能量,发出的能量只被两边最近的且比它高的发射站接收。显然,每个发射站发来的能量有可能被 \(0\) 或 \(1\) 或 \(2\) 个其他发射站所接受。
请计算出接收最多能量的发射站接收的能量是多少。
输入格式:第 \(1\) 行一个整数 \(N\)。第 \(2\) 到 \(N+1\) 行,第 \(i+1\) 行有两个整数 \(H_i\) 和 \(V_i\),表示第 \(i\) 个人发射站的高度和发射的能量值。
输出格式:输出仅一行,表示接收最多能量的发射站接收到的能量值。答案不超过 32 位带符号整数的表示范围。
| 输入样例 | 输出样例 |
|---|---|
3 4 2 3 5 6 10 |
7 |
【数据范围】\(1\le N\le 10^6,1\le H_i\le 2\times 10^9,1\le V_i\le 10^4\)。
【分析】
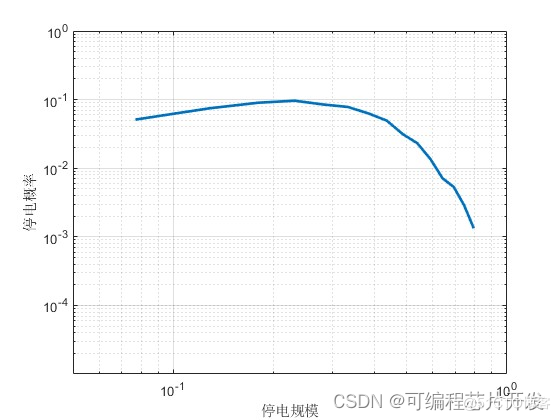
- 法1:直接暴力模拟,左右查找合适的值,可以过 40%,会 TLE。
- 法2:维护单调栈(单调递减栈:栈底到栈顶元素单调递减)
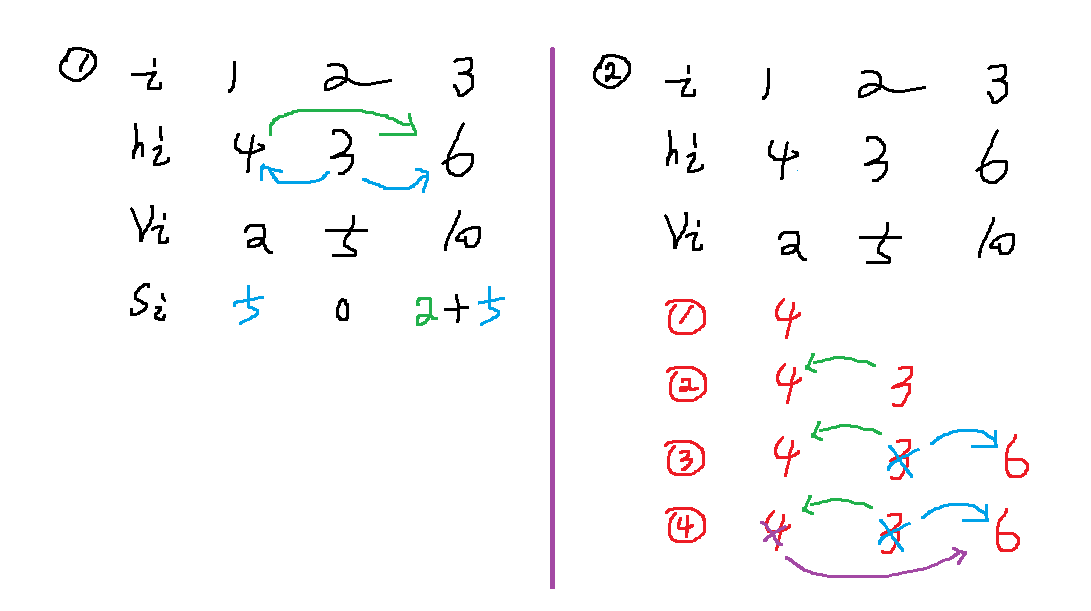
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,h[N],v[N],st[N],head=0;
LL ans[N];void slove1() { // 预计 TLEfor(int i=1; i<=n; i++) {int l=i-1, r=i+1;while(l>0 && h[l]<=h[i]) l--;while(r<=n && h[r]<=h[i]) r++;ans[l]+=v[i], ans[r]+=v[i];}
}
void slove2() { // 维护一个单调栈for(int i=1; i<=n; i++) {while(head && h[st[head]] < h[i]) {ans[i] += v[st[head]], head--;}ans[st[head]] += v[i];st[++head] = i;}
}
int main() {scanf("%d",&n);for(int i=1; i<=n; i++) scanf("%d%d",&h[i],&v[i]);slove1();for(int i=1; i<=n; i++) ans[1]=max(ans[1],ans[i]);printf("%lld\n",ans[1]);return 0;
}
P1540 [NOIP2010 提高组] 机器翻译
- P1540 [NOIP2010 提高组] 机器翻译
P2085 最小函数值
- P2085 最小函数值
P6033 [NOIP2004 提高组] 合并果子 加强版
- P6033 [NOIP2004 提高组] 合并果子 加强版
P1631 序列合并
- P1631 序列合并
P2251 质量检测
- P2251 质量检测
P1305 新二叉树
- P1305 新二叉树
B3631 单向链表
- B3631 单向链表
P1739 表达式括号匹配
- P1739 表达式括号匹配
P1996 约瑟夫问题
- P1996 约瑟夫问题
n 个人围成一圈,从第一个人开始报数,数到 m 的人出列,再由下一个人重新从 1 开始报数,数到 m 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
输入格式:输入两个整数 n,m(1≤m,n≤100)。
输出格式:输出一行 n 个整数,按顺序输出每个出圈人的编号。
输入样例:10 3
输出样例:3 6 9 2 7 1 8 5 10 4
点击查看代码
#include<bits/stdc++.h>
using namespace std;
queue<int> que;
int main(){int n,m,cnt=1; cin>>n>>m;for(int i=1; i<=n; i++) que.push(i);while(!que.empty()){if(cnt<m){que.push(que.front());que.pop(); cnt++;}else if(cnt==m){cout<<que.front()<<" ";que.pop(); cnt=1;}} return 0;
}
P1808 单词分类
- P1808 单词分类
【题目描述】
两个单词可以分为一类当且仅当组成这两个单词的各个字母的数量均相等。
例如 "AABAC",它和 "CBAAA" 就可以归为一类,而和 "AAABB" 就不是一类。
现在Oliver有N个单词,所有单词均由大写字母组成,每个单词的长度不超过100。
你要告诉Oliver这些单词会被分成几类。
【输入格式】输入文件的第一行为单词个数N,以下N行每行为一个单词。
【输出格式】输出文件仅包含一个数,表示这N个单词分成的类数
| 输入样例 | 输出样例 |
|---|---|
3 AABAC CBAAA AAABB |
2 |
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+1;
char s[N][101];
int main(){int n; cin>>n;for(int i=1; i<=n; i++){scanf("%s", s[i]);sort(s[i], s[i]+strlen(s[i]));}map<string,int> m;for(int i=1; i<=n; i++){m.insert(pair<string,int>(s[i],1));}printf("%d", m.size());return 0;
}
B3616 【模板】队列
- B3616 【模板】队列
P3378 【模板】堆
- P3378 【模板】堆
给定一个数列,初始为空,请支持下面三种操作:
- 给定一个整数 x,请将 x 加入到数列中。
- 输出数列中最小的数。
- 删除数列中最小的数(如果有多个数最小,只删除 1 个)。
输入格式:第一行是一个整数,表示操作的次数 n。
接下来 n 行,每行表示一次操作。每行首先有一个整数 op 表示操作类型。
若 op=1,则后面有一个整数 x,表示要将 x 加入数列。
若 op=2,则表示要求输出数列中的最小数。
若 op=3,则表示删除数列中的最小数。如果有多个数最小,只删除 1 个。
输出格式:对于每个操作 2,输出一行一个整数表示答案。
| 输入样例 | 输出样例 |
|---|---|
5 1 2 1 5 2 3 2 |
2 5 |
点击查看代码
#include<iostream>
#include<queue>
using namespace std;
priority_queue<int, vector<int>, greater<int> > pq;
//priority_queue<int, vector<int>, less<int> > pq;
int main(){int n; cin>>n;for(int i=1; i<=n; i++){int f; cin>>f;if(f==1){int x; cin>>x; pq.push(x);}else if(f==2){cout<<pq.top()<<endl;}else if(f==3){pq.pop();}} return 0;
}
P4715 【深基16.例1】淘汰赛
- P4715 【深基16.例1】淘汰赛
有 2^n(n≤7) 个国家参加世界杯决赛圈且进入淘汰赛环节。
我经知道各个国家的能力值,且都不相等。能力值高的国家和能力值低的国家踢比赛时高者获胜。
1 号国家和 2 号国家踢一场比赛,胜者晋级。3 号国家和 4 号国家也踢一场,胜者晋级……晋级后的国家用相同的方法继续完成赛程,直到决出冠军。
给出各个国家的能力值,请问亚军是哪个国家?
| 输入样例 | 输出样例 |
|---|---|
3 4 2 3 1 10 5 9 7 |
1 |
点击查看代码
#include<iostream>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
int main() {int n; cin>>n; n = pow(2, n); // n=1<<n;queue<pair<int, int> > que;for(int i=1; i<=n; i++) {int a; cin>>a; que.push(make_pair(i, a));}while( que.size() > 2 ){pair<int, int> x,y;x = que.front(); que.pop();y = que.front(); que.pop();if(x.second > y.second) que.push(x);else que.push(y);}pair<int, int> x,y;x = que.front(); que.pop();y = que.front(); que.pop();if(x.second > y.second) cout<<y.first;else cout<<x.first;return 0;
}