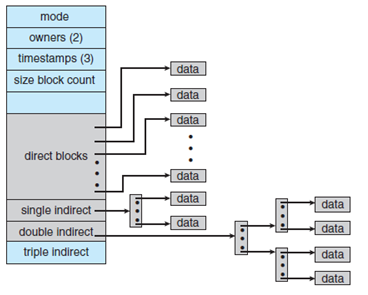
时间复杂度
运行时间可以直观且准确地反映算法的效率。要准确预估一段代码的运行时间,应该进行如下操作。
- 确定运行平台,包括硬件配置、编程语言、系统环境等,这些因素都会影响代码的运行效率。
- 评估各种计算操作的运行时间,例如加法操作需要1ns,乘法操作需要10ns,打印操作需要5ns等。
- 统计代码中所有的计算操作,并将所有操作的执行时间求和,从而得到运行时间。
// 在某运行平台下
void algorithm(int n) {int a = 2; // 1 nsa = a + 1; // 1 nsa = a * 2; // 10 ns// 循环 n 次for (int i = 0; i < n; i++) { // 1 ns ,每轮都要执行 i++std::cout << 0 << std::endl; // 5 ns}
}根据以上方法,可以得到算法的运行时间为(6n+12)ns
但时间上,统计算法的运行时间既不合理也不现实。首先,我们不希望将预估时间和运行平台绑定,因为算法需要在各种不同的平台上运行。其次我们很难获知每种操作的运行时间,这给预估过程带来了极大的难度。
统计时间增长趋势
时间复杂度分析统计的不是算法运行时间,而是算法运行时间随着数据量变大时的增长趋势。
“时间增长趋势”这个概念比较抽象,我们通过一个例子来加以理解。假设输入数据大小为n,给定三个算法A、B、C:
// 算法 A 的时间复杂度:常数阶
void algorithm_A(int n) {cout << 0 << endl;
}
// 算法 B 的时间复杂度:线性阶
void algorithm_B(int n) {for (int i = 0; i < n; i++) {cout << 0 << endl;}
}
// 算法 C 的时间复杂度:常数阶
void algorithm_C(int n) {for (int i = 0; i < 1000000; i++) {cout << 0 << endl;}
}- 算法A只有一个打印操作,算法运行时间不随着n增大而增大。我们称此算法的时间复杂度为“常数阶”。
- 算法B中的打印操作需要循环n次,算法运行时间随着n增大而线性增加。此算法的时间复杂度被称为“线性阶”。
- 算法C中的打印操作需要循环1000000次,虽然运行时间很长,但是它与输入数据大小n无关。因此C的时间复杂度与A相同,均为“常数阶”。

函数渐近上界
给定一个输入大小为n的函数:
void algorithm(int n) {int a = 2; // +1 a = a + 1; // +1 a = a * 2; // +1// 循环 n 次for (int i = 0; i < n; i++) { // +1 ,每轮都要执行 i++std::cout << 0 << std::endl; // +1}
}设算法的操作数量是一个关于输入数据大小n的函数,记为 𝑇(𝑛),则以上函数的操作数量为:
𝑇(𝑛) = 3 + 2𝑛
𝑇(𝑛) 是一次函数,说明其运行时间的增长趋势是线性的,因此它的时间复杂度是线性阶。
我们将线性阶的时间复杂度记为 𝑂(𝑛) ,这个数学符号称为大O记号,表示函数 𝑇(𝑛) 的渐近上界(asymptotic upper bound)。
时间复杂度分析本质上是计算“操作数量𝑇(𝑛)”的渐近上界,它具有明确的数学定义。
推算方法
总体上分为两步:首先统计操作数量,然后判断渐近上界。
第一步:统计操作数量
针对代码,逐行从上到下计算即可。操作数量𝑇(𝑛)中的各种系数、常数项都可以忽略。根据此原则,可总结出一下计数简化技巧。
- 忽略𝑇(𝑛)中的常数项。
- 省略所有系数。
- 嵌套循环时使用乘法。总操作数量等于外层循环和内层循环操作数量之积。
void algorithm(int n) {int a = 1; // +0(技巧 1)a = a + n; // +0(技巧 1)// +n(技巧 2)for (int i = 0; i < 5 * n + 1; i++) {cout << 0 << endl;}// +n*n(技巧 3)for (int i = 0; i < 2 * n; i++) {for (int j = 0; j < n + 1; j++) {cout << 0 << endl;}}
} 以下公式展示了使用上述技巧前后的统计结果,两者推算出的时间复杂度都为 𝑂(𝑛2
) 。
𝑇(𝑛) = 2𝑛(𝑛 + 1) + (5𝑛 + 1) + 2 完整统计 (‑.‑|||)
= 2n2 + 7𝑛 + 3
𝑇(𝑛) = 𝑛2 + 𝑛 偷懒统计 (o.O)
第二步:判断渐近上界
时间复杂度由𝑇(𝑛)中最高阶的项来决定。这是因为在n趋于无穷大时,最高阶的项将发挥主导作用,其他项的影响都可以忽略。
下表展示了一些例子,其中一些夸张的值是为了强调“系数无法撼动阶数”这一结论。

常见类型
设输入数据大小为n,常见的时间复杂度类型如图所示:


常数阶 𝑂(1)
常数阶的操作数量与输入数据大小n无关,即不随着n的变化而变化。
线性阶 𝑂(n)
线性阶的操作数量相对于数据大小n以线性级别增长。通常出现在单层循环中。遍历数组和遍历链表等操作的时间复杂度均为 𝑂(𝑛) ,其中n为数组或链表的长度。
平方阶 𝑂(n2)
平方阶通常出现在嵌套循环中,外层循环和内层循环的时间复杂度都为 𝑂(𝑛) ,因此总体的时间复杂度为 𝑂(𝑛2) 。
以冒泡排序为例,外层循环执行n-1次,内层循环执行n-1、n-2、n-3、...、2、1次,平均n/2次,因此时间复杂度为 𝑂((𝑛 − 1)𝑛/2) = 𝑂(𝑛2)
/*平方阶-冒泡排序*/
int bubbleSort(vector<int> &nums){/*for (int i = 0; i < nums.size(); i++){for (int j = i + 1; j < nums.size(); j++){if (nums[i] > nums[j]){int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}}}*/for (int i = 0; i < nums.size(); i++){for (int j = 0; j < nums.size() - i - 1; j++){if (nums[j] > nums[j + 1]){int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}
}指数阶 𝑂(2n)
生物学的“细胞分裂”是指数阶增长的典型例子:初识状态为1个细胞,分裂一轮后变为4个,以此类推,n轮分裂后有2n个细胞。
在实际算法中,指数阶常出现于递归函数中。

/* 指数阶(循环实现) */
int exponential(int n) {int count = 0, base = 1;// 细胞每轮一分为二,形成数列 1, 2, 4, 8, ..., 2^(n-1)for (int i = 0; i < n; i++) {for (int j = 0; j < base; j++) {count++;}base *= 2;}// count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1return count;
}
/* 指数阶(递归实现) */
int expRecur(int n) {if (n == 1)return 1;return expRecur(n - 1) + expRecur(n - 1) + 1;
}指数阶增长非常迅速,在穷举(暴力搜索、回溯等)中比较常见。对于数据规模较大的问题,指数阶是不可接受的,通常需要使用动态规划或贪心算法等来解决。
对数阶 𝑂(log 𝑛)
与指数阶相反,对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为n,由于每轮缩减到一半,因此循环次数是log2n

与指数阶类似,对数阶也常出现于递归函数中。以下代码形成了一棵高度为log2n的递归树:
/* 对数阶(递归实现) */
int logRecur(int n) {if (n <= 1)return 0;return logRecur(n / 2) + 1;
}对数阶常出现于基于分治策略的算法中,体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢,是仅次于常数阶的理想的时间复杂度。
线性对数阶 𝑂(𝑛 log 𝑛)
线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别是𝑂(log 𝑛) 和 𝑂(𝑛)
如图展示了线性对数阶的生成方式。二叉树的每一层的操作总数都为n,树共有 log2𝑛 + 1 层,因此时间复杂度为𝑂(𝑛 log 𝑛) 。

主流排序算法的时间复杂度通常为𝑂(𝑛 log 𝑛),例如快速排序、归并排序、堆排序等。
阶乘阶𝑂(𝑛!)
阶乘对应数学上的“全排列”问题。给定n个互不重复的元素,求其所有可能的排列方案,方案数量为:
𝑛! = 𝑛 × (𝑛 − 1) × (𝑛 − 2) × ⋯ × 2 × 1
阶乘通常使用递归实现:
/* 阶乘阶(递归实现) */
int factorialRecur(int n) {if (n == 0)return 1;int count = 0;// 从 1 个分裂出 n 个for (int i = 0; i < n; i++) {count += factorialRecur(n - 1);}return count;
}