相交两圆

这篇写的太早了，我自己也看不懂，现在找不到啥基础题适合放了。反正把构型掌握了就好。

Reim引理

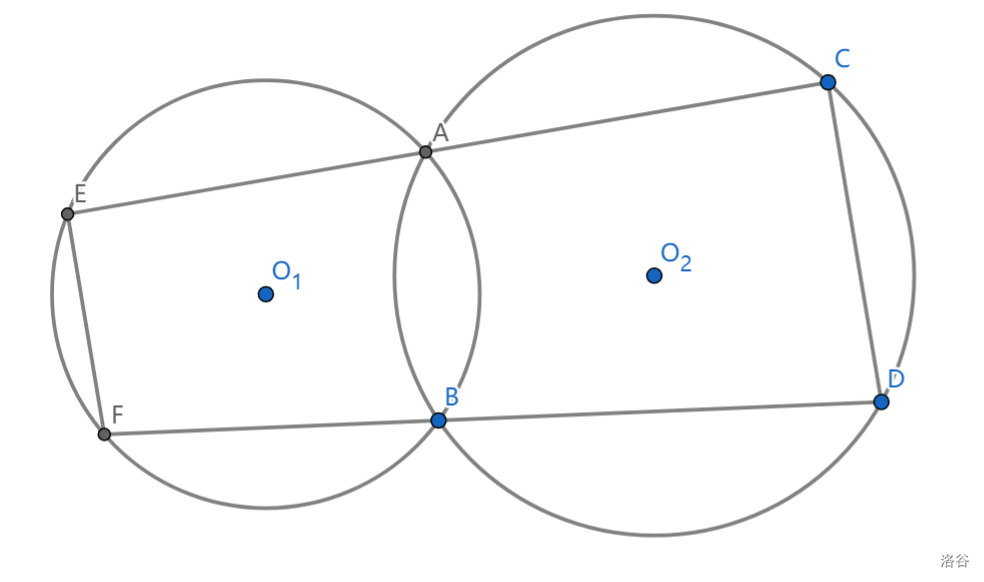
如图，两圆交于 \(A,B\) 两点，若 \(CD,EF\) 是两圆的弦，满足 \(CAE,DBF\) 分别共线，则 \(CD//EF\)

逆定理：若 \(ABCD\) 共圆，\(E,F\) 分别在 \(CA,DB\) 的延长线上，并满足 \(EF//CD\) ，则 \(ABEF\) 也共圆

表述 \(2\) ：若 \(ABCD,ABEF\) 分别共圆， \(EF//CD\) ，若 \(ACE\) 共线，则 \(BFD\) 共线

\(Reim\) 引理有多种构型

（圆内接四边形+平行=共圆）

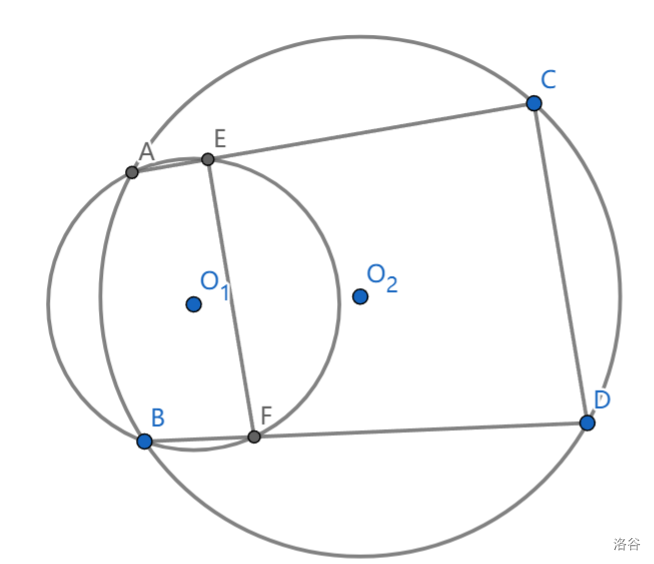
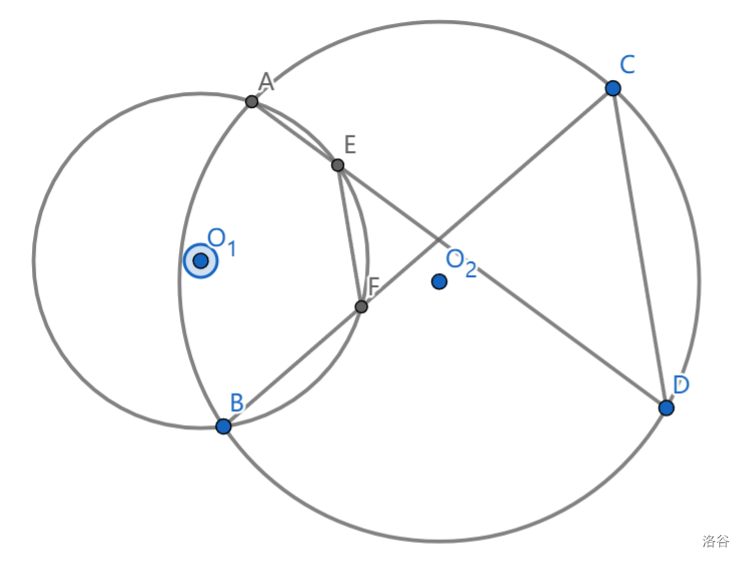
如果觉得难记：我们可以把共圆的对边理解为逆平行，两次逆平行会变为正平行，一次正平行+一次逆平行=逆平行

例1

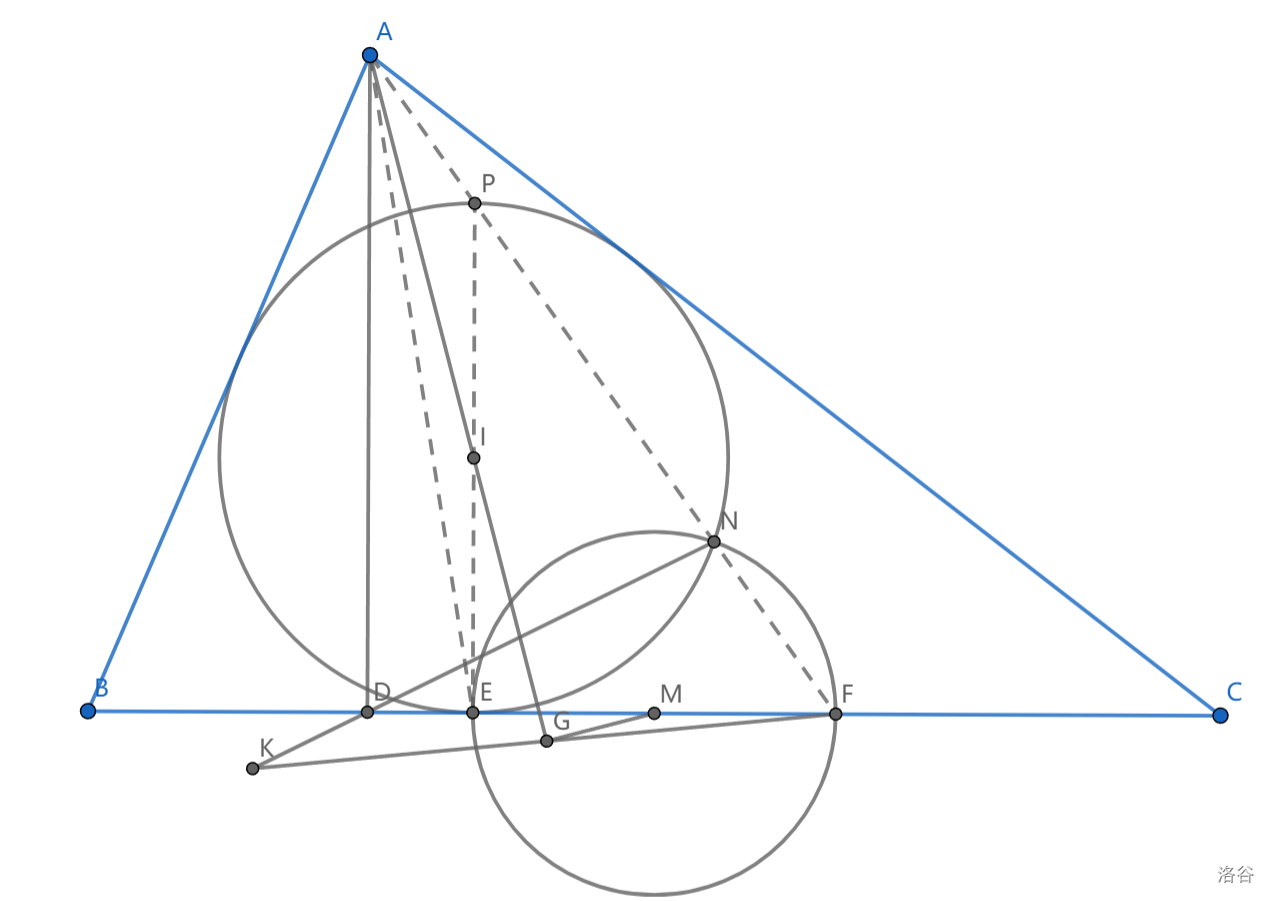
如图，\(AD\perp BC\) 于点 \(D\) ， \(\triangle ABC\) 内切圆 \(I\) 切 \(BC\) 于点 \(F\) ，\(M\) 为 \(BC\) 中点，以 \(M\) 为圆心， \(ME\) 为半径画圆交圆 \(I\) 与 \(BC\) 于 \(N,F\) ，作 \(MG\perp AI\) 于点 \(G\) ，延长 \(FG,ND\) 交于点 \(K\) ，求证： \(D,E,K,G\) 共圆

注意到 \(IMEG\) 共圆，又 \(IM//PF\) ，即 \(AFEG\) 共圆 （ \(Reim\) 引理）

又 \(EP\) 为圆 \(I\) 的直径，可知 \(\angle ANE=\angle ANE=Rt\angle\) ，即 \(ANED\) 共圆

那么 \(\angle K=\pi-\angle DNF-\angle AFG=\angle AND-(\pi-\angle AEG)=\angle AED+\angle AEG-\pi =\angle FEG\)

即证

旋转相似

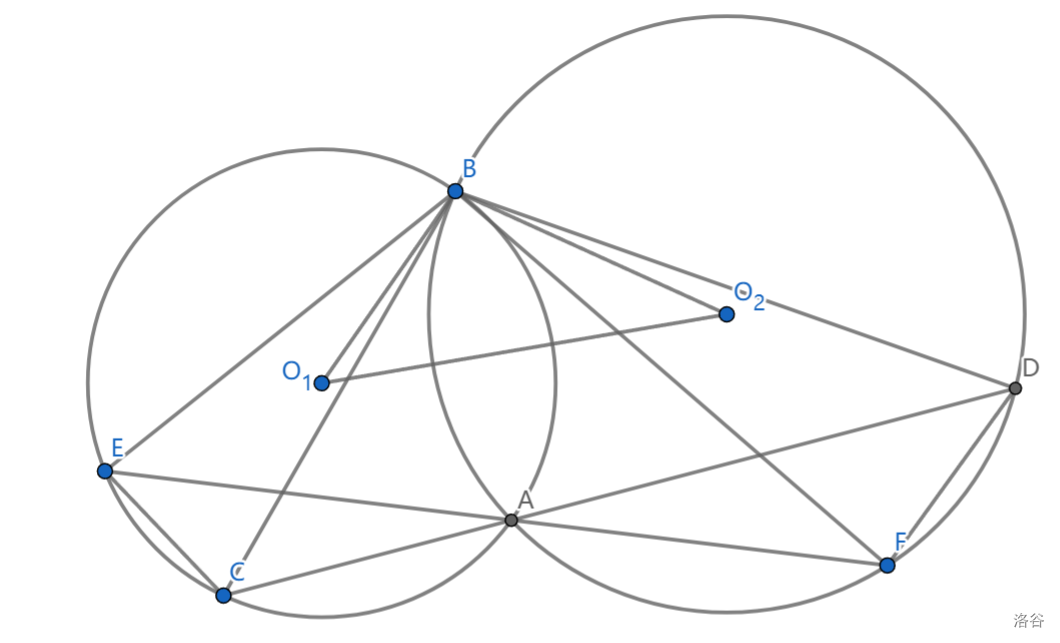
如图，有 \(\triangle BEF\sim\triangle BCD\sim\triangle BO_1O_2,\triangle BEC\sim \triangle BFD\)

当然有这个相似和其中一个共圆能推另一个共圆

这个构型与密克点也有关系

例1

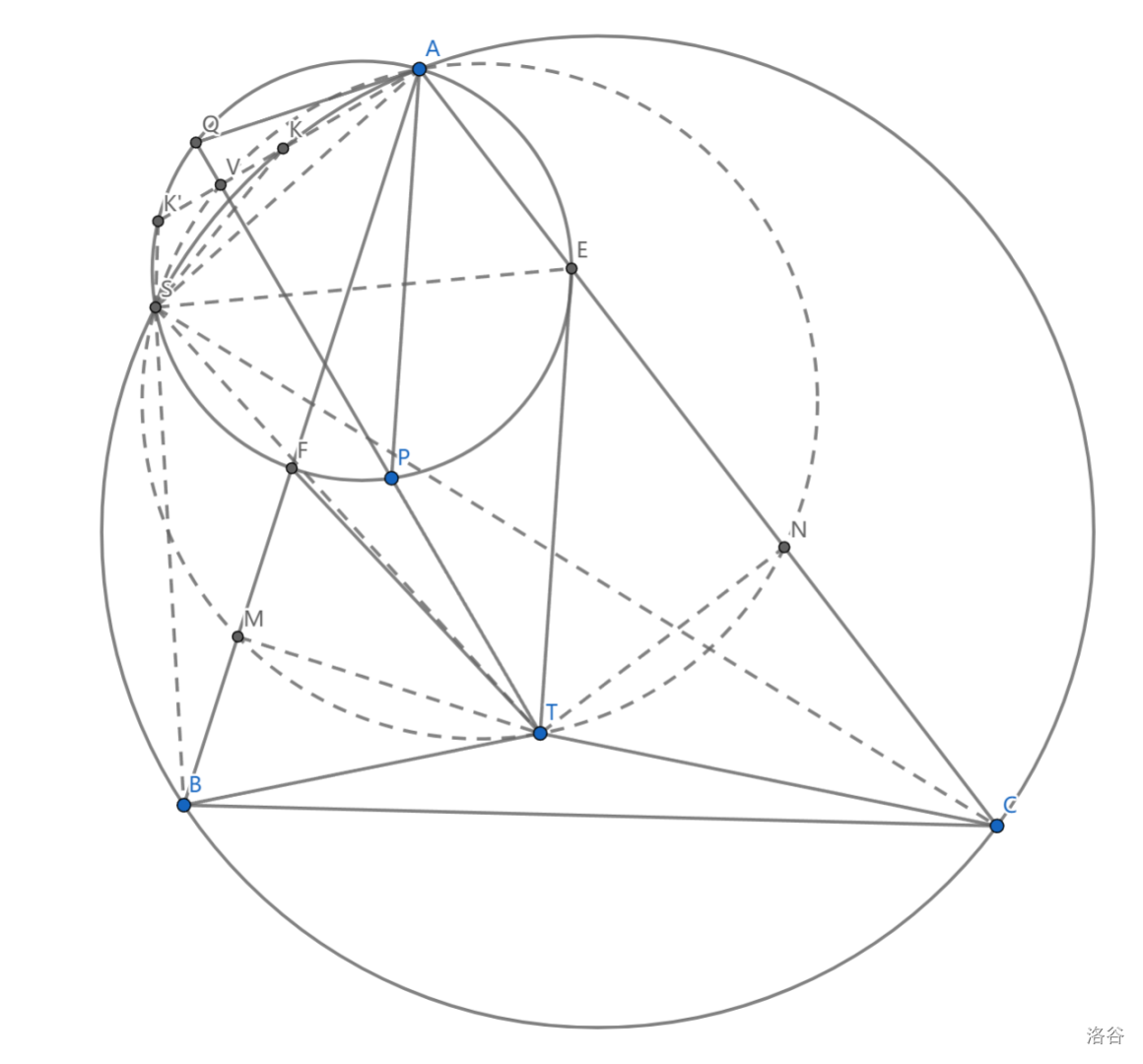
如图 ，\(\triangle ABC\) 内接于圆 \(\Omega\) ， \(T\) 是 \(\triangle ABC\) 内部任一点， 点 \(E,F\) 分别在 \(AB,AC\) 上，且满足 \(TB=TF,TC=TE\) ， \(TPQ\) 是 \(\triangle AEF\) 外接圆的一条割线，证明： \(\triangle APQ\) 的垂心在 \(\Omega\) 上

过 \(A\) 做 \(PQ\) 垂线，与 \(\Omega\) 及 \(\odot(AEF)\) 交于点 \(K,K'\) 。题目即要求证 \(K\) 为垂心，而 \(K'\) 是垂心关于 \(PQ\) 的对称点，因此考虑记 \(V=AK\cap PQ\)

取出 \(BF,CE\) 中点 \(M,N\) ，实际上 \(AMTN\) 共圆，不难注意到三圆共轴，下面来证明这一点：

记 \(S=\Omega\cap\odot(AEF)\) ，根据经典模型，有 \(\triangle SBF(M)\sim\triangle SCE(N)\)

从而 \(\angle SMF=\angle SNE\) ，即 \(S\) 也在 \(\odot(AMN)\) 上

由于 \(\angle AST=Rt\angle=\angle AVT\) ，从而 \(AVSMTN\) 共圆

根据经典模型 \(\triangle SBF(M)\sim\triangle SCE(N)\sim\triangle SKK'(V)\)

即 \(KV=K'V\) ，则知 \(K\) 为垂心

例2

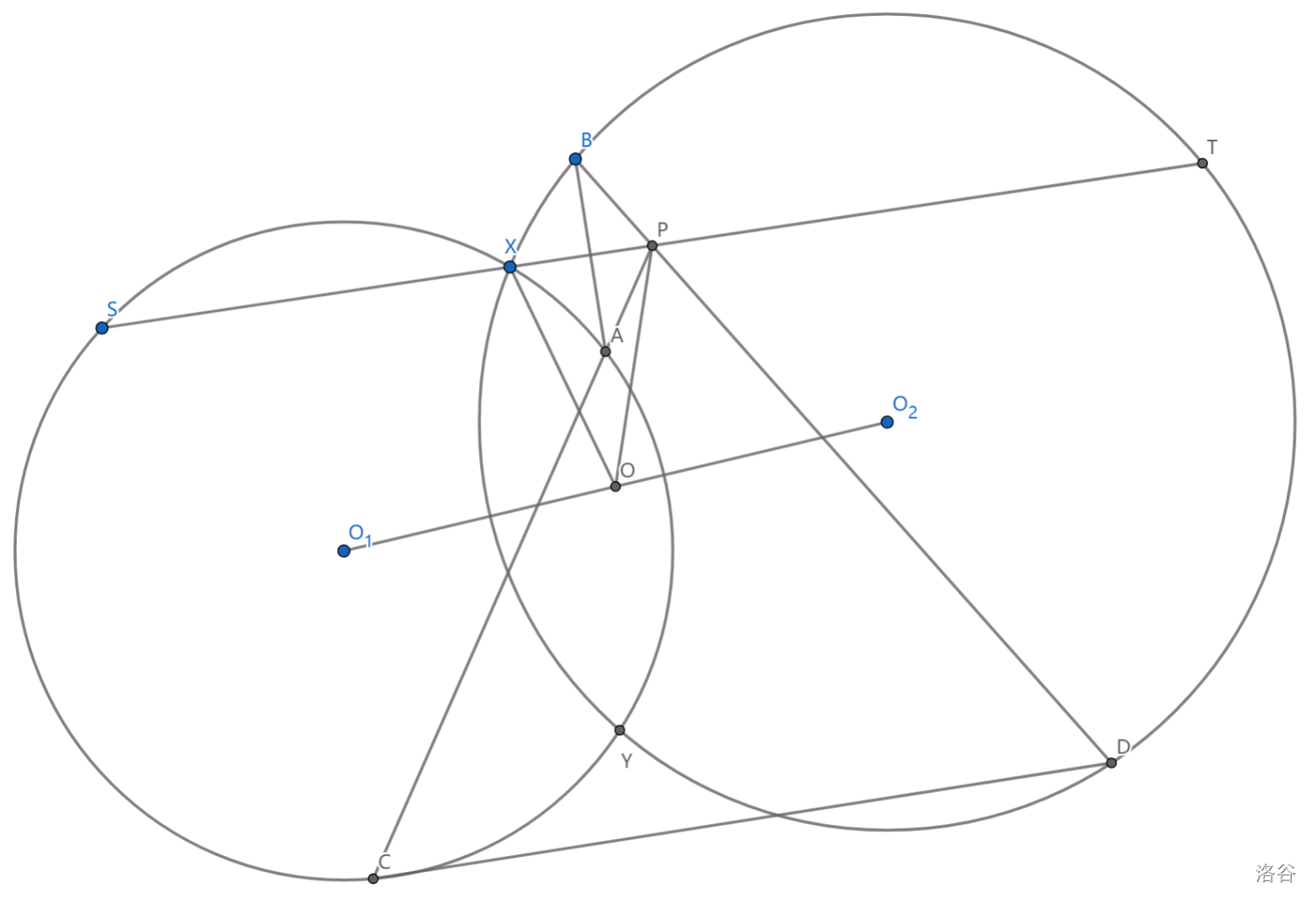
如图，\(\odot O_1,\odot O_2\) 交于点 \(X,Y\) ，弦 \(BD,AC\) 分别在 \(\odot O_2,\odot O_1\) 上并交于点 \(P\) ，满足 \(PA-PB,PC=PD\) ，记 \(O\) 为 \(O_1O_2\) 中点，求证： \(O\) 为 \(\triangle PXY\) 的外心

由经典模型可以得到一个引理：如图，若 \(P\) 为 \(ST\) 中点，则 \(OP=OX\)

证明是不困难的，只要注意到 \(\triangle YO_1O_2(O)\sim\triangle YST(P)\) ，则得到 \(\triangle YO_1S\sim\triangle YOP\sim\triangle YO_2T\)

回到原题，已知条件即 \(P\) 对于两圆的圆幂为相反数

根据中线定理知我们需要证明 \(2(O_1P^2+PS^2)=O_1S^2+O_1T^2,2(O_2P^2+PS^2)=O_2S^2+O_2T^2\)

两式相加得到 \(2(O_1P^2+O_2P^2)+ST^2=R_1^2+R_2^2+O_1T^2+O_2S^2\) 这个命题和 \(P\) 是中点是等价的

实际上 \(O_1R^2+O_2R^2,R\in ST\) 是一个二次函数，而 \(O_1P^2+O_2P^2=O_1X^2+O_2X^2\) （由上述引理结合中线定理即可得知），这意味着 \(P,X\) 是上述方程的唯二解，而 \(X\) 在两圆上的幂为 \(0\) ，舍

我们先证明 \(O_1T^2+O_2S^2=R_1^2+R_2^2+ST^2\)

由余弦定理， \(ST^2+O_1S^2-2O_1S\cdot ST \cdot cos\angle O_1ST =O_1T^2\)

\(ST^2+O_2T^2-2O_2T\cdot ST\cdot cos\angle O_2TS=O_2S^2\)

两式相加，我们只需证 $ST^2=2ST(O_1Scos\angle O_1ST+O_2Tcos\angle O_2TS) $ ，显然成立

又 \(P\) 对两圆圆幂为相反数 \(\iff O_1P^2+O_2P^2=R_1^2+R_2^2\) 两式相加即证

例3

给定 \(\triangle ABC\) ，求点 \(P\in BC\) 满足若 \((APB),(APC)\) 的两条外公切线与 \(AP\) 交点为 \(X,Y\) ，则 \((\frac{PA}{XY})^2+\frac{PB\cdot PC}{AB\cdot AC}=1\)

这题很简单，唯一的难点是容易想复杂。我们看到

\(\large 1-(\frac{PA}{XY})^2=\frac{4XA\cdot XP}{XY}=(\frac{XM}{XL})^2\)

是定值。我们还看到 \(\triangle O_1O_2T\sim \triangle ZXL\) ，所以 \(\frac{XL}{2XM}=\frac{XL}{GT}=\frac{XZ}{O_1O_2}=\frac{O_1A+O_2A}{XZ}\) ，用到了梯形中位线

现在用旋转相似 \(\triangle AO_1O_2\sim \triangle ABC\) ，所以 \(\frac{XL}{XM}=\frac{AB+AC}{BC}\)

然后 \(\frac{PB\cdot PC}{AB\cdot AC}=(\frac{BC}{AB+AC})^2\) ，有一个点满足这个条件，就是角平分线与 \(BC\) 交点。当然它关于 \(BC\) 中点的对称点也满足条件。

圆幂分析

在多圆问题中巧妙利用圆幂分析也是相当重要的方法

例1

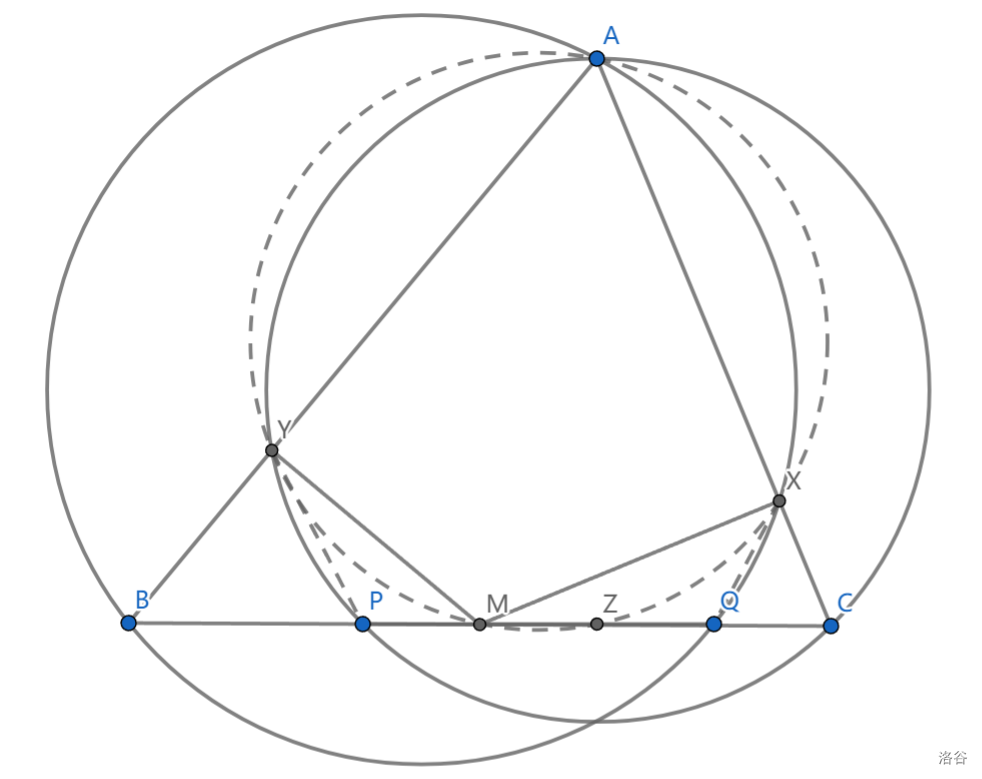
\(M\) 是 \(BC\) 中点，\(P,Q\) 是 \(BC\) 上两点，满足 \(PQ=\frac12BC\) ，\(X,Y\) 分别是 \(\triangle ABQ,\triangle ACP\) 外接圆与 \(AC,AB\) 的交点，求证： \(AXMY\) 共圆

取 \(Z\) 使得 \(CQ=QZ\) ，那么 \(CZ\cdot CM=CQ\cdot CB=CX\cdot CA\) ，即 \(AXZM\) 共圆，同理 \(AYZM\) 共圆，即证