粒子群优化函数--particleswarm函数的用法与讨论

news/2024/9/21 12:26:52/文章来源:https://www.cnblogs.com/dlmuwxw/p/18369846

particleswarm函数是matlab自带的粒子群优化算法，其使用自适应的邻域模式搜索最优解，比我们之前自己写的代码要好得多，本章我们来讨论一下其思想与参数设置

一、自适应的邻域模式
- 1.全局模式与邻域模式
- 2.全局模式的优劣
- 3.邻域模式的优劣
- 4.何为“自适应”
二、预设参数的选取
- 1.粒子个数SwarmSize
- 2.惯性权重与学习因子
- 3.邻域内粒子的比例MinNeighborsFraction
三、自动退出迭代循环
- 1.最大停滞迭代次数与容忍度
- 2.最大迭代次数
- 3.可视化迭代图形
- 4.混合函数求解
四、代码求解极值问题
- 1.函数语法
- 2.问题提出
- 3.代码求解
五、修改函数的参数
- 1.绘制最佳的函数值随迭代次数的变化图
- 2.展示函数的迭代过程
- 3.修改粒子数量
- 4.在粒子群算法结束后继续调用其他函数进行混合求解
- 5.最大的迭代次数
- 6.领域内粒子的比例
- 7.函数容忍度与最大停滞迭代数
六、函数参数修改的建议

一、自适应的邻域模式

在我们前面对粒子群算法的优化讨论中，核心思想就是根据不同的情况，修改惯性权重w，与c1和c2。而matlab自带的算法使用的调整参数的方法则更加先进

1.全局模式与邻域模式

在观察鸟群觅食的过程中注意到,通常飞鸟并不一定看到鸟群中其他所有飞鸟的位置和方向,往往只是看到相邻的飞鸟的位置和方向。因此他在研究粒子群算法时,同时开发了两种模式:全局模式(gbest)和邻域模式(lbest)

2.全局模式的优劣

全局模式是指粒子群在搜索过程中将所有其他粒子都视为邻域粒子,它可以看做是邻域模式的极端情况,基本粒子群算法即属于全局模式。其优点是粒子邻域个体多,粒子群内的信息交流速度快,使得粒子群算法具有较快的收敛速度,但在一定程度上会降低粒子多样性,易陷人局部最优。

3.邻域模式的优劣

邻域模式是指粒子群在搜索过程中只将其周围部分粒子视为邻域粒子,这种模式使得粒子群可以被分割成多个不同的子群体,有利于在多个区域进行搜索,避免算法陷人局部最优。

4.何为“自适应”

自适应体现在:如果适应度开始停滞时，粒子群搜索会从邻域模式向全局模式转换。一旦适应度开始下降，则又恢复到邻域模式，以免陷入局部最优。当适应度的停滞次数足够大时，惯性系数开始逐渐变小，从而利于局部搜索。搜索初期使用邻域模式较好，后期使用全局模式

二、预设参数的选取

1.粒子个数SwarmSize

默认设置为：min{100,10*nvars}, nvars是变量个数

2.惯性权重与学习因子

惯性权重InertiaRange默认设置的范围为：[0.1,1.1]，个体学习因子SelfAdjustmentWeight与社会学习因子SocialAdjustmentWeight默认设置为：1.49 （和压缩因子的系数几乎相同）

3.邻域内粒子的比例MinNeighborsFraction

默认设置为：0.25，由于采取的是邻域模式，因此定义了一个“邻域最少粒子数目”：minNeighborhoodSize = max{2,(粒子数目*邻域内粒子的比例)的整数部分}，在迭代开始后，每个粒子会有一个邻域，初始时邻域内的粒子个数(记为Q)就等于“邻域最少粒子数目”，后续邻域内的粒子个数Q会自适应调整。

三、自动退出迭代循环

Matlab自带的粒子群函数可以设置几种自动退出迭代循环的方法

1.最大停滞迭代次数与容忍度

MaxStallIterations and FunctionTolerance；前者为最大停滞迭代次数，默认为20，也就是说迭代20次后，适应度没有优化则退出迭代。后者为容忍度，默认为1e-6；
Exit Flag=1；其为跳出参数

2.最大迭代次数

MaxIterations；默认值为200*nvars，若超过这个数，则退出迭代
Exit Flag=0；

3.可视化迭代图形

OutputFcn or PlotFcn；在迭代的过程中看到图形，可以随时暂停和停止
Exit Flag=-1；

4.混合函数求解

MaxTime；如果是第一种方式退出迭代的话，我们可以将粒子群算法得到的解作为初始值，继续调用其他的函数来进行混合求解，例如我们熟悉的fmincon函数(我测试发现以第二种退出好像也可以调用求他函数混合求解)
Exit Flag=-5

四、代码求解极值问题

1.函数语法

由于matlab只能求最小值问题，如果求最大值的话要在目标函数前加负号
[x,fval,exitflag,output] = particleswarm(@Obj_fun2, narvs, x_lb, x_ub)
输入的第一个参数是我们的一个函数文件，用@符号来引导；第二个参数则是变量的个数；第三第四个分别为上下界。
输出的前两个变量即为我们的变量取值与函数值。第三个变量是一个常数，其意义是告诉我们迭代是从种情况跳出的；
第四个变量为一个结构体，我们只需要关注两个信息。（1）iterations为迭代的次数（2）message，告诉我们以何种方式跳出迭代

2.问题提出

求解函数y = x1^2+x22-x1x2-10x1-4*x2+60在[-15,15]内的最小值（最小值为8）

3.代码求解

narvs = 2; % 变量个数
x_lb = [-15 -15]; % x的下界(长度等于变量的个数，每个变量对应一个下界约束)
x_ub = [15 15]; % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun2, narvs, x_lb, x_ub)

五、修改函数的参数

1.绘制最佳的函数值随迭代次数的变化图

options = optimoptions('particleswarm','PlotFcn','pswplotbestf')   
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

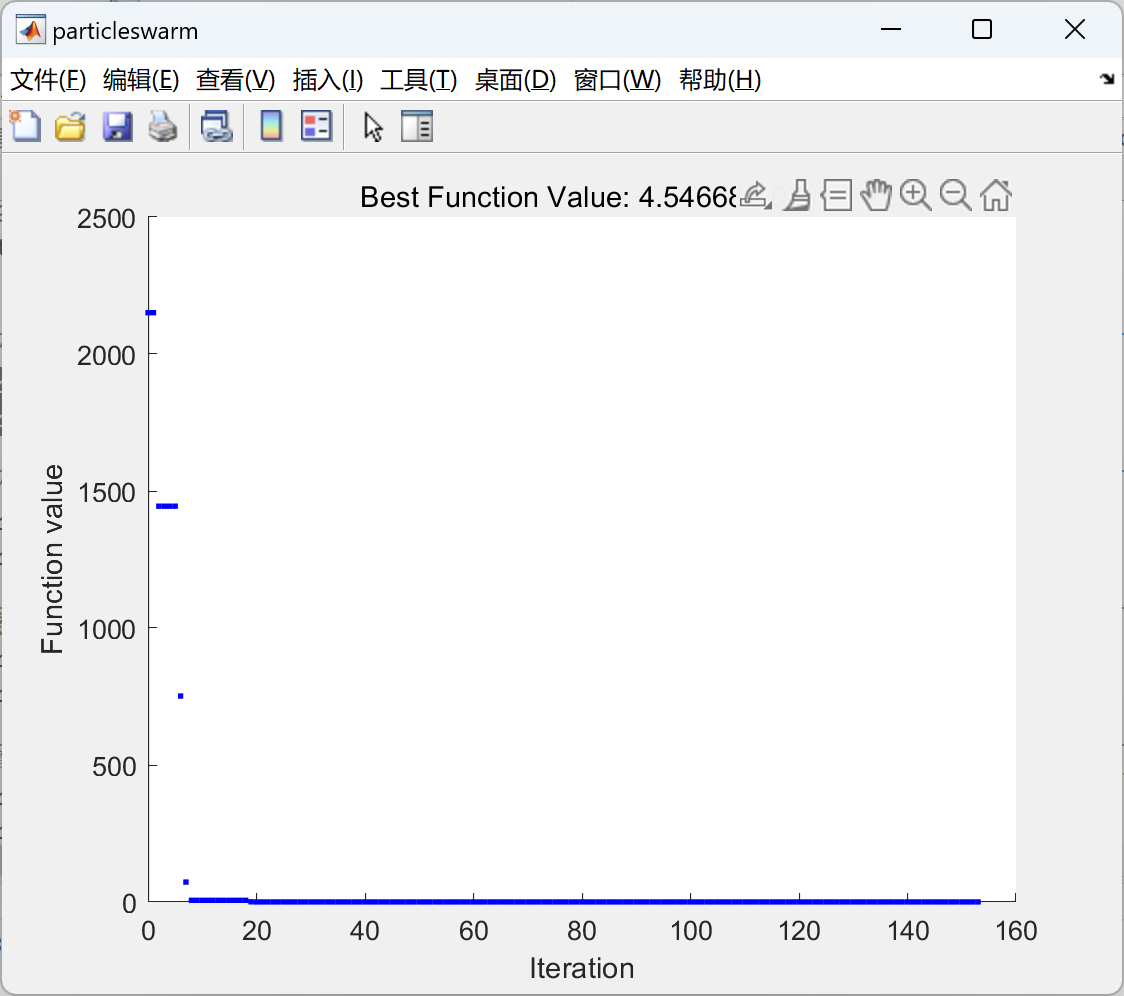
2.展示函数的迭代过程

在matlab下方的输出框展示每次迭代的结果

options = optimoptions('particleswarm','Display','iter');
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

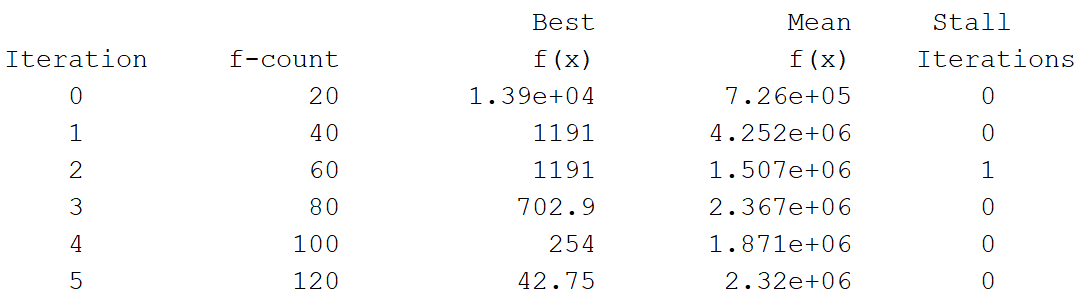
3.修改粒子数量

options = optimoptions('particleswarm','SwarmSize',50); %默认的是：min(100,10*nvars)
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

4.在粒子群算法结束后继续调用其他函数进行混合求解

options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

5.最大的迭代次数

options = optimoptions('particleswarm','MaxIterations',10000); %，默认的是200*nvars
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

6.领域内粒子的比例

options = optimoptions('particleswarm','MinNeighborsFraction',0.2); %默认是0.25 
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

7.函数容忍度与最大停滞迭代数

options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100); % 默认1e-6与20
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)