卡特兰数、Prufer 序列、BSGS 总结

卡特兰数

定义

给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，它们构成一个长度为 \(2n\) 的排列，满足任意前缀中 \(0\) 的个数都不少于 \(1\) 的个数的序列的数量为卡特兰数列。显然 \(H_0=H_1=1\)。（\(H\) 为卡特兰数列）

通项公式：

\[H_n=\frac{\dbinom{2n}{n}}{n+1}\quad (n\ge2,n\in\mathbf N_+) \]

递推公式：

\[\begin{aligned} H_n&=\begin{cases}\displaystyle\sum_{i=1}^nH_{i-1}H_{n-i}&n\ge2,n\in\mathbf N_+\\1&n=0,1\end{cases} \\ &=\frac{H_{n-1}(4n-2)}{n+1} \\ &=\binom{2n}n-\binom{2n}{n-1} \end{aligned} \]

卡特兰数：

\[H=\{1,1,2,5,14,42,132,\dots\} \]

一些结论

1. 在直角坐标系上，每一步只能向上或向右走，从 \((0,0)\) 走到 \((n,n)\) 并且除两端点为不越过直线 \(y=x\) 的路线数量为 \(2H_{n-1}\)。
2. 同上问题，从 \((0,0)\) 走到 \((n,m)\) 并且不接触直线 \(y=x\) 的路线数量为 \(2\dbinom{2n-2}{n-1}-2\dbinom{2n-2}{n}\)。
3. 同上问题，从 \((0,0)\) 走到 \((n,m)\) 并且不越过直线 \(y=x\) 的路线数量为 \(\dbinom{n+m}{n}-\dbinom{n+m}{n+1}\)。
4. \(n\) 个左括号和 \(n\) 个右括号组成的合法括号序列数量为 \(H_n\)。
5. \(1,2,\dots,n\) 经过一个栈，形成的合法出栈序列的数量为 \(H_n\)。
6. \(n\) 个结点构成的不同二叉树的数量为 \(H_n\)。

卡特兰数问题特征

计数问题、排列等，都是卡特兰数问题的特征。

遇到这类可以向卡特兰数方向考虑的问题，可以先手推一遍前几个数，看是否符合卡特兰数列。很多题看着复杂，实际上就是卡特兰数模板题。

有些题不给模数，容易酿成高精度，需要注意。一般高精度的处理方法就是分解质因数，化高精乘除法为加减法，最后只需要一个高精乘低精就可解决。顶多再写一个高精加减低精就可以。笔者在刚打到这里时总是想着码一个万能高精模板出来，但最后发现不仅码量庞大且没有必要，更多时候还是见招拆招，万能模板看似适用，实际上实用性低。

Prufer 序列

Prufer 序列是一种将带标号的树用唯一的一个整数序列表示的方法，二者一一对应。不考虑含有一个结点的树。

定义

Prufer 序列可以将一个 \([1,N]\) 结点的树用 \((N-2)\) 个整数表示。Prufer 是这样建立的：每次选择一个编号最小的叶结点并删掉它，然后在序列中记录下它连接到的那个结点。重复 \((N-2)\) 次后就只剩下两个结点，算法结束。

这是一棵 \(7\) 个结点的树的 Prufer 序列构建过程：

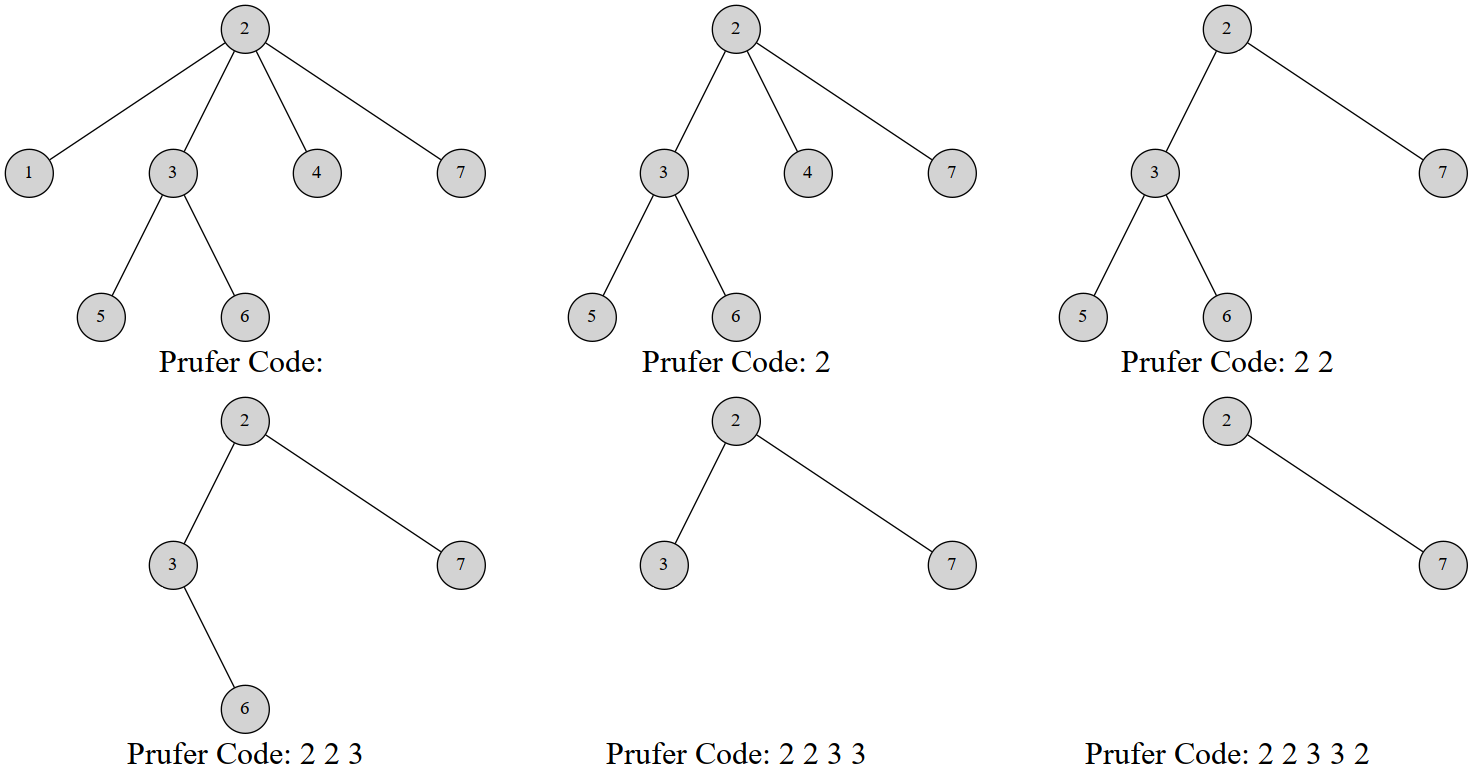
对树建立 Prufer 序列

用堆可以做到 \(O(N\log N)\) 的复杂度，但存在线性构造算法。

线性构造的本质就是维护一个指针指向我们将要删除的结点。首先发现，删去一个叶结点，叶结点总数要么不变要么减 \(1\)。

于是维护一个指针 \(p\) 指向编号最小的叶节点。每次删掉它之后，如果产生了新的叶节点且编号比 \(p\) 指向的更小，则直接继续删掉，重复这一流程。最后 \(p\) 自增找到下一个编号最小的叶节点。

正确性

\(p\) 已经是当前编号最小的叶节点。如果删 \(p\) 后产生了新的叶节点 \(x\)，若 \(x>p\) 不置可否，反正 \(p\) 往后都会扫描到它；但若 \(x<p\)，则 \(x\) 成为当前编号最小的叶节点，应优先加入序列。易得 \(p\) 最多遍历每个结点一次，所以复杂度 \(O(N)\)。

实现

void solve1() {for (int i = 1; i <= n - 1; i++) cin >> fa[i], deg[fa[i]]++;for (int i = 1, p = 1; i <= n - 2; i++, p++) {while (deg[p]) p++; // 自增找到下一个叶子结点pf[i] = fa[p]; // 加入序列while (i <= n - 2 && --deg[pf[i]] == 0 && pf[i] < p) // 如果产生新叶子结点且编号更小pf[i + 1] = fa[pf[i]], i++;}
}

Prufer 序列重构树

与上面同理的，逆运算。注意因为 Prufer 序列只有 \((N-2)\) 位，而我们要生成的树的父亲序列是 \((N-1)\) 位的，所以要给 Prufer 序列加一位 \(\text{pf}_{N-1}=N\)。

void solve2() {for (int i = 1; i <= n - 2; i++) cin >> pf[i], deg[pf[i]]++;pf[n - 1] = n;for (int i = 1, p = 1; i <= n - 2; i++, p++) {while (deg[p]) p++;fa[p] = pf[i];while (i <= n - 2 && --deg[pf[i]] == 0 && pf[i] < p)fa[pf[i]] = pf[i + 1], i++;}
}

Prufer 序列的性质

1. 构造完 Prufer 序列后原树会剩下两个结点，其中一个一定是编号最大的结点 \(N\)。
2. 每个结点在序列中出现的次数是其度数减 \(\boldsymbol1\)。（没有出现的就是叶节点）

第二点十分重要，是后文的依据。

凯莱公式

完全图 \(\boldsymbol{K_n}\) 有 \(\boldsymbol{n^{n-2}}\) 棵生成树。

用 Prufer 序列证明十分容易。首先，完全图，说明每个结点都有可能出现在 Prufer 序列的每个位置上。最重要的是，从图推树，形态是不限的，也就是说哪怕是 \((n-2)\) 个 \(1\) 也可以，这样推出来的就是一个以 \(1\) 为根结点的 \((n-1)\) 叉树。（带点感性理解，关键是后面有一个易混公式）

一些结论

1. 一个 \(\boldsymbol n\) 个点 \(\boldsymbol m\) 条边的带标号无向图有 \(\boldsymbol k\) 个连通块，我们希望添加 \(\boldsymbol{(k-1)}\) 条边使图联通。方案数为:

\[n^{k-2}\cdot\prod_{i=1}^ks_i \]

其中 \(s_i\) 表示每个连通块的大小。

2. 一个无向连通图在给定所有点度情况下的生成树数量为：

\[\frac{(n-2)!}{\prod_{i=1}^n(\textit{deg}_i-1)!} \]

理解 1：由 Prufer 序列性质 2，度数为 \(\textit{deg}_i\) 的点在序列中出现 \((\textit{deg}_i-1)\) 次。给定了每个点的度数，所以这个序列的大小为 \(n-2\) 的可重集是一定的。换句话说，这个序列的每一项都是确定的，情况的不同只是其排列数。每一种排列都对应一种生成树，所以总情况数就是多重组合数，全排列个数除以内部排列个数。

理解 2：尝试解释凯莱公式中的 \(n^{n-2}\) 和本题中的 \((n-2)!\)。因为凯莱公式是由完全图推 Prufer 序列，其序列本身是不确定的，每个位置都有 \(n\) 种情况且可以重复，自然就是 \(n^{n-2}\)。而这里给的信息相当于是确定了 Prufer 序列的所有元素，所以是其内部排列即 \((n-2)!\)。

3. 同上问题，只给定某些点的度数 \(\boldsymbol{\boldsymbol{deg}_i}\)，求生成树数量为：

\[\frac{\left(\prod_{t=n-1-s}^{n-2}t\right)(n-k)^{n-2-s}}{\prod_{i=1}^k\left(\textit{deg}_i-1\right)!},s=\sum_{i=1}^k(\textit{deg}_i-1) \]

具体参考这篇题解。

总而言之，Prufer 序列本质上是一个工具，其发明出来的目的就是为了证明凯莱公式，本身意义不大。Prufer 序列给我们的帮助更多的是提供了一种解决关于树的计数问题的思路，而不在于其与树的编解码过程（当然代码也不难背是吧。

BSGS

BSGS 算法，全称 Baby Step, Giant Step 算法，是一种用于求解形如 \(a^x\equiv b\pmod p\) 的高次同余方程的算法，要求 \(a\perp p\)，否则可以用 exBSGS 算法。算法的时间复杂度是 \(O(\sqrt p)\)。

原理

因为 \(a,p\) 互质，所以可以在模 \(p\) 意义下执行关于 \(a\) 的乘除法运算。

设 \(x=it-j\)，其中 \(t=\left\lceil\sqrt p\right\rceil\)，\(0\le j\le t-1\)，则方程变为 \(a^{it-j}\equiv b\pmod p\)，即 \(a^{it}\equiv b\times a^j\pmod p\)。

对于所有的 \(j\in[0,t-1]\)，把 \(b\times a^j\) 插入一个 Hash 表，可以用 unordered_map 实现。

枚举 \(i\) 的所有可能取值，即 \(i\in[0,t]\)，计算出 \(a^{it}\bmod p\)，在 Hash 表中查找是否存在对应的 \(j\)，更新答案即可。

实现

int bsgs(int a, int b, int p) {unordered_map<int, int> h;h.clear();b %= p;int t = ceil(sqrt(p));for (int j = 0; j < t; j++) {int val = b * power(a, j, p) % p;h[val] = j;}a = power(a, t, p);if (a == 0) return b == 0 ? 1 : -1;for (int i = 0; i <= t; i++) {int val = power(a, i, p);int j = h.find(val) == h.end() ? -1 : h[val];if (j >= 0 && i * t - j >= 0) return i * t - j;}return -1;
}

代码视为加入了 #define int long long。

坑点

若 \(\boldsymbol{b=1}\)，需特判输出 \(\boldsymbol0\)。