Pollard Rho 算法

news/2024/9/18 8:54:43/文章来源:https://www.cnblogs.com/zsk123qwq/p/18377009

Pollard Rho 算法

难评，看OI-WIKI吧。

引入

Pollard Rho 算法用于求快速找到一个正整数 $n$ 的一个非平凡因数^[1]。

生日悖论

不考虑出生年份（假设每年都是365天），问：一个房间中至少多少人，才能使其中两个人生日相通的概率达到 $50\%$？

解：假设一年有 $n$ 天，房间中有 $k$ 人，用 $1$ 到 $k$ 给这些人编号。假定每个人的生日均与分布于 $n$ 天之中，且两个人的生日相互独立。设 $k$ 个人生日互不相同的时间为 $A$，则 $P(A)=\prod_{i=0}^{k-1}\frac{n-i}{n}$。然后烂糟推一堆得出：

\[\exp(-\frac{k(k-1)}{2n})\le \frac{1}{2}\Rightarrow P(A)\le\frac{1}{2} \]

将 $n=365$ 代入，解得 $k \ge 23$。所以一个房间中至少有 $23$ 人，使其两人生日相同的概率达到 $50\%$，但这个数学事实非常反直觉，故称之为一个悖论。当 $k>56,n=365$ 时，出现两个人同一天生日的概率将大于 $99\%$！

利用最大公约数求出一个约数

首先明确 $n$ 和某个数的最大公约数一定是 $n$ 的约数。我们可以通过 $f(x)=(x^2+c)\bmod n$ 来生成一个序列 ${x_i}$：随机选取一个 $x_i$，令 $x_2=f(x_1),x_3=f(x_2),\dots,x_i=f(x_{i-1})$。其中 $c$ 是一个随机选取的常熟。

举个例子，设 $n=50,c=6,x_1=1$，$f(x)$ 生成的数据为 $1,7,5,31,17,45,31,17,45,31,\dots$ 可以发现数据在 $x_4$ 以后都在 $31,17,45$ 循环。如果将这些数如下图一样排列起来，就发现他是一个这个玩意儿，长得像一个 $\rho$，所以这个算法得名 rho。

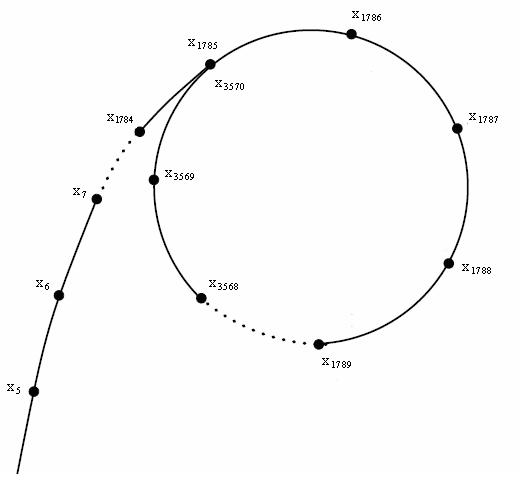
$Pollard-rho1.png (520×480) (oi-wiki.org)$

选择 $f(x)=(x^2+c)\bmod n$ 作为这个生成函数序列，是因为它有一个性质：$\forall x \equiv y \pmod p,f(x)\equiv f(y)\pmod p$，其中 $p \mid n$。

证明

若 $x=y \pmod p$，则可以将它们表示为 $x=k_1p+a,y=k_2p+a$，满足 $k_1,k_2,a \in \mathbb{Z},a \in [0,p)$。

$f(x)=(x^2+c)\bmod n$，因此 $f(x)=x^2+c-kn$，其中 $k\in\mathbb{Z}$。

\[\begin{align} f(x) & = x^2+c-kn\\ & = (k_1p+a)^2+c-kn\\ & = k_1^2p^2+2k_1pa+a^2+c-kn\\\ & \equiv a^2+c \end{align} \]
同理， $f(y)\equiv a^2+c \pmod p$，因此 $f(x) \equiv f(y) \pmod p$。

根据生日悖论，生成的序列中不同值的数量约为 $\sqrt{n}$ 个。设 $m$ 为 $n$ 的最小非平凡因子，显然有 $m \le \sqrt{n}$。将 ${x_i}$ 中每一项对 $m$ 取模，我们得到了一个新序列 ${y_i}$，并且根据生日悖论可以得知新序列中不同值的个数约为 $O(\sqrt m) \le O(n^{\frac{1}{4}})$。因此，我们可以在期望 $O(n^{\frac{1}{4}})$ 的时间内找到两个位置 $i,j$，使得 $x_i\ne x_j \&\& y_i=y_j$，这意味着 $n \nmid |x_i-x_j| \&\& m\mid |x_i-x_j|$，我们可以通过 $\gcd(n,|x_i-x_j|)$ 获得 $n$ 的一个非平凡因子。

代码实现

#include <bits/stdc++.h>
#define int long longusing namespace std;
mt19937 wdz(time(0)); // 随机数
int N;
int gcd(int n, int m) {return m == 0 ? n : gcd(m, n % m);
}
int pollard(int n, int c) {int x, y, d, i = 1, k = 2;x = wdz() * wdz() % (n - 1) + 1; // 此处的 wdz() 是随机数y = x;while (1) {x = (x * x % n + c) % n;d = gcd((x - y + n) % n, n);if (1 < d && d < n) return d;if (x == y) return n;// x = y 说明构成了一个环，说明选定的 c 不好，那么重新来一遍if (++i == k) {k <<= 1;y = x;// 由于 y 不一定在环内，所以随时更新 y 的值，不然会死循}}return 23333333;
}
signed main() {scanf("%lld", &N);p = N;while (p >= N) {p = pollard(N, wdz() * wdz() % (n - 1) + 1);}// p 为 N 的一个因子printf("%lld\n", p);return 0;
}