198 打家劫舍
func rob(nums []int) int {// 思路,动态规划// dp[i] 代表前下标为i能装的最大盗窃物品价值// 递推 dp[i] = max(dp[i-1], dp[i-2]+v(i)) // dp[i-1] 代表不偷物品i, dp[i-2]+v(i) 代表偷物品i,那么就不能偷i-1,因为题目要求不能相邻,所以考虑前i-2// dp[0] = 0, dp[1] = nums[0]// 正序遍历物品// printvar dp = make([]int, len(nums)+1)dp[0] = 0dp[1] = nums[0]for i := 1; i < len(nums); i++ {dp[i+1] = max(dp[i], dp[i-1]+nums[i])}fmt.Println(dp)return dp[len(nums)]
}
213 打家劫舍||
func rob(nums []int) int {// 相比打家劫舍1 多出一个限制就是首位相连,所以,我们划分两个数组,包含首,以及包含尾,然后对比// dp[i] 表示前i个房间偷盗最大金额// dp[i] = max(dp[i-1], dp[i-1]+v(i))// dp[0]=0, dp[1] = nums[0]// 遍历房间// printlength := len(nums)if length == 1{return nums[0]}var dp1 = make([]int, length) // 顾首不顾尾var dp2 = make([]int, length) // 顾尾不顾首dp1[1] = nums[0]dp2[1] = nums[1]for i := 1; i < length -1 ; i++ {dp1[i+1] = max(dp1[i], dp1[i-1]+nums[i])dp2[i+1] = max(dp2[i], dp2[i-1]+nums[i+1])}//fmt.Println(dp1, dp2)if dp2[length-1] > dp1[length-1]{return dp2[length-1]}return dp1[length-1]
}
337 打家劫舍|||
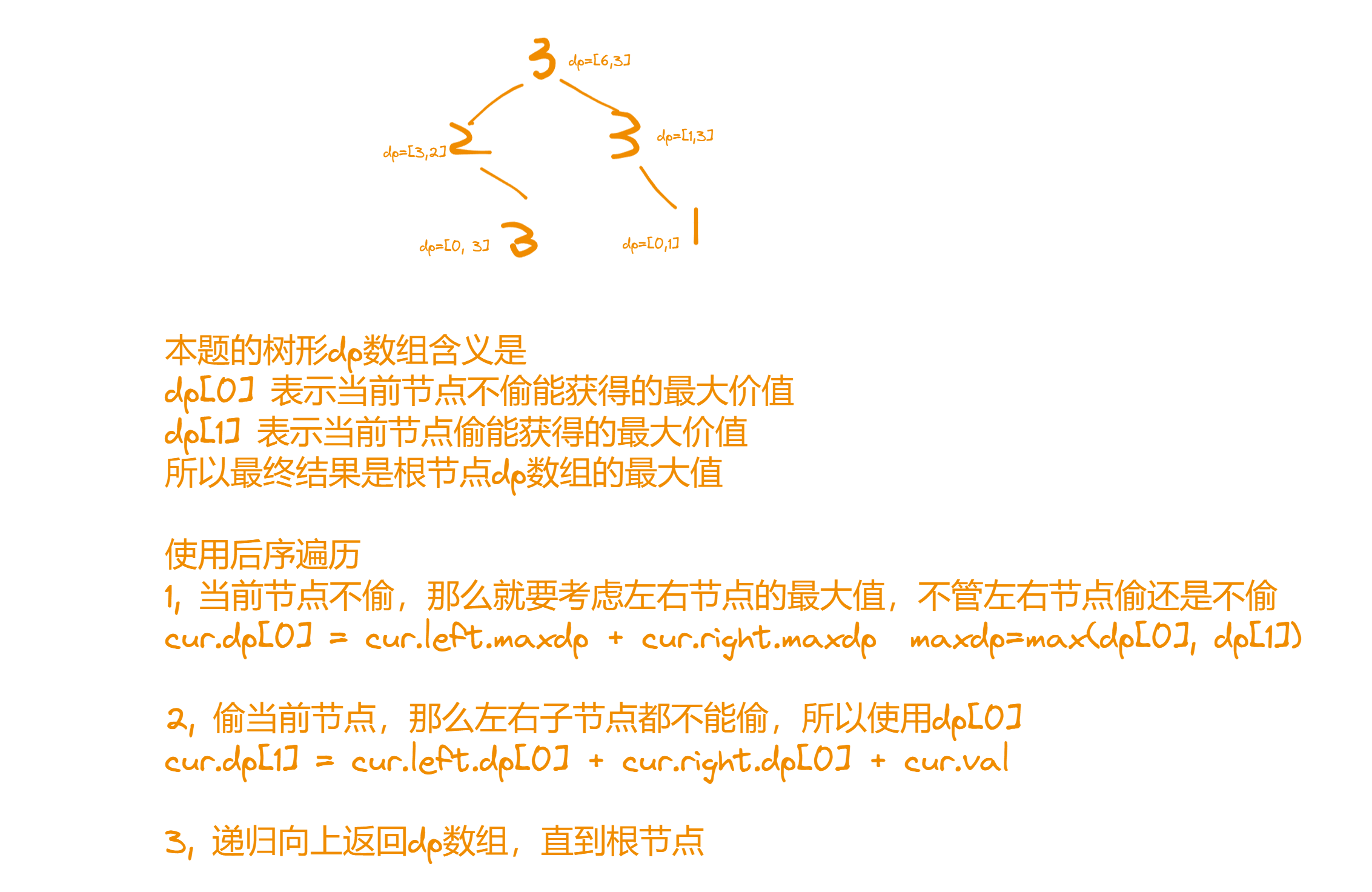
func rob(root *TreeNode) int {// 本题在于树形dp的定义以及递推公式,还要结合树的遍历顺序// dp = [2]int{} ,dp[0] 表示不偷取当前节点, dp[1] 表示偷当前节点// 递推公式:// cur.dp[0] = cur.left.maxdp + cur.right.maxdp maxdp=max[dp[0],dp[1]]// cur.dp[1] = cur.left.dp[0] + cur.right.dp[0] + cur.Val// 初始化,空节点dp = [0,0]// 树后序遍历// printres := robTree(root)return max(res)
}func robTree(cur *TreeNode) [2]int {var dp = [2]int{}if cur == nil {return dp}var leftDP, rightDP [2]int// leftif cur.Left != nil {leftDP = robTree(cur.Left)}// rightif cur.Right != nil {rightDP = robTree(cur.Right)}// rootdp[0] = max(leftDP) + max(rightDP)dp[1] = leftDP[0] + rightDP[0] + cur.Val//fmt.Println(cur.Val, dp[0], dp[1])return dp
}
func max(res [2]int) int {if res[0] > res[1] {return res[0]}return res[1]
}