DIN
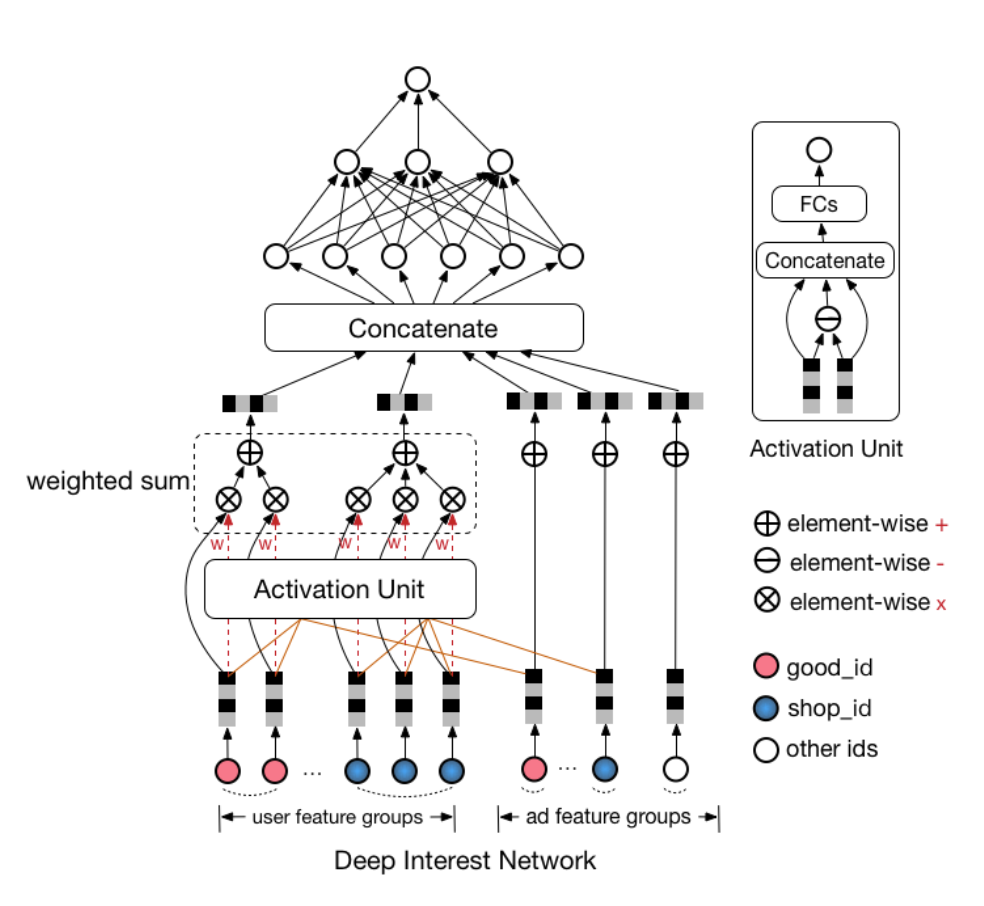
假设 \(V_i^{shop},V_i^{good},V_i^{cate}\) 分别表示历史第 \(i\) 次点击的 shop_id,good_id,cate_id, \(V_a^{shop},V_a^{good},V_a^{cate}\) 分别表示候选商品的 shop_id,good_id,cate_id,则两个不同版本用户兴趣表达 \(V_u\) 计算方式如下
DIN的优缺点
- 缺点
- 用户兴趣应该是不断进化的。DIN抽取的用户兴趣是固定的,没有捕获到兴趣的这种进化性
- 如何保证通过用户的显式的行为得到的兴趣是有效的(不太明白)
参考资料:
- https://blog.csdn.net/u012328159/article/details/123043033
- https://zhuanlan.zhihu.com/p/103092757?utm_medium=social&utm_psn=1811383167061475328&utm_source=wechat_session
GAUC
DIN在模型的评估上,定义了 GAUC:
其中 \(n\)表示用户数, \(\text{impression}_i\) 和 \(AUC_i\)分别表示第 \(i\) 个用户的曝光和 AUC,新的 AUC 更贴近线上真实情况,因为最终我们是按每个用户进行排序的。
GAUC的缺点:
- GAUC是单用户的sample求auc以后再平均,但是单用户行为没有那么多的时候,会抖动
参考资料:https://blog.csdn.net/qfikh/article/details/105390002
AUC
- ROC曲线:ROC曲线的横坐标是FPR(表示实际为负的样本有多少预测成了正),纵坐标是TPR(表示实际为正的样本有多少预测成了正)。对于一个分类器的输出通常是概率阈值。通过改变阈值大小,会输出不同的FPR和TPR的值,将其连接起来则得到ROC曲线
AUC 的计算公式
接下来,我们解释一下这个公式:
P:表示正样本
N:表示负样本
|P|:表示正样本数量
|N|:表示负样本数量
| \(rank_{i}\) |:表示根据模型的预测分数排行,i 号样本的顺序编号。
好的,我们来看一下,这个公式是怎么推演出来的?
| 编号 | 样本 | 模型预测值 |
|---|---|---|
| 1 | p1 | 0.25 |
| 2 | p2 | 0.3 |
| 3 | n1 | 0.4 |
| 4 | p4 | 0.80 |
| 5 | n2 | 0.80 |
| 6 | n3 | 0.80 |
| 7 | p5 | 0.85 |
| 8 | n4 | 0.89 |
| 9 | n5 | 0.95 |
| 10 | p3 | 0.96 |
假如我们现在存在 10 个样本,并且模型对 10 个正样本都给出了对应的预测值,最后我们还按照模型的预测值的大小进行了排序。那么 \(rank_{i}\)rank_{i} 即表示样本排序后的编号。
好,我们说:
AUC 等于随机挑选一个正样本和负样本时,模型对正样本的预测分数大于负样本的预测分数的概率。
对于预测概率第 1 大的正样本,也就是编号为 10 的样本,在上表中对应 P1,那么比他小的负样本的个数为 \(rank_{n} - (\left| P \right|)\)。
对于预测概率第 2 大的正样本,也就是编号为 7 的样本,在上表中对应 P5,那么比他小的负样本的个数为 \(rank_{n-1} - (\left| P \right| - 1)\)。
找规律一直下去:
对于预测概率最小的正样本,比他小的负样本的个数为 \(rank_{1} - 1\) 。
好的,那么这样其实分子就出来了,我们把他们加和处理。
那我们只需要求解分母就可以了,任意去一个正样本和一个负样本,共有 \(|P|\times|N|\) 种方案。
那么现在这个公式是不是就表示,挑选一个正样本和负样本,正样本的预测分数大于负样本的预测分数的概率了呢?
\(AUC = \frac{\sum_{a\in P}^{}{rank_i}-\frac{|P|*(|P|+1)}{2}}{|P|*|N|}\)
那么,我们计算一下改表格对应的 AUC 是多少?
| 编号 | 样本 | 预测分数 |
|---|---|---|
| 1 | p1 | 0.25 |
| 2 | p2 | 0.3 |
| 3 | n1 | 0.4 |
| 4 --> 5 | p4 | 0.80 |
| 5 --> 5 | n2 | 0.80 |
| 6 --> 5 | n3 | 0.80 |
| 7 | p5 | 0.85 |
| 8 | n4 | 0.89 |
| 9 | n5 | 0.95 |
| 10 | p3 | 0.96 |
可以看到,这里面包含了一些预测分数相等的行,对于这样的数据,我们只需要对编号进行加和重新平均即可。将编号4、 5、6 替换成 5。
好的,代公式:
参考资料:https://zhuanlan.zhihu.com/p/361214293
AUC 含义的理解
注:下面的说明不是严格的证明,只是帮助通俗理解。
那么,应该怎么将 AUC 的值与概率联系起来呢?首先,我们知道整个区域的面积是 1。假设正样本的数量为 \(M\) ,负样本数量为 \(N\),并且在改变阈值的过程中,每当一个样本从被预测为正,变为被预测为负,则:
- 若此样本为正样本,则 TPR 将减小 \(\frac{1}{M}\)
- 若此样本为负样本,则 FPR 将减小 \(\frac{1}{N}\)
由于每让一个样本的预测结果发生变化,都画出了一条线段,因此让每个样本对应一条线段,负样本对应上方水平的线段,正样本对应右侧垂直的线段。于是可以将整个区域划分为 \(M\times N\) 个小区域,每个区域可以由一条垂直的线段和一条水平的线段通过平移组成,那么这个区域就可以代表这两条线段对应的一个正样本和一个负样本组成的样本对,如下图。
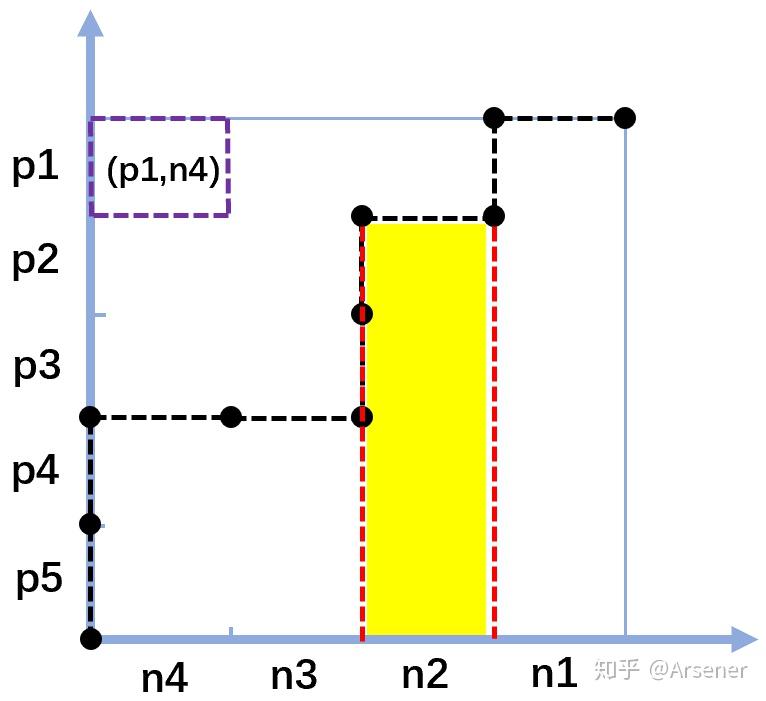
那么我们来理解一下图中黄色区域代表什么?这个黄色部分代表的其实是所有得分比 n2 的得分高的正样本与 n2 组成的样本对。也就是说黄色的部分由 4 个小块组成,每个小块是一个样本对,在这个样本对中,正样本的得分比负样本得分高。
所以,我们可以得到结论,ROC 曲线下面的所有小块代表的样本对都是正样本得分比负样本得分高的样本对。而我们也可以证明 ROC 上面的所有小块代表的样本对都是正样本得分比负样本得分低的样本对。
现在,你能否理解 AUC 的含义了呢:随机给定一个正样本和一个负样本,用一个分类器进行分类和预测,该正样本的得分比该负样本的得分要大的概率。
而根据这一含义,我们也可以确定,AUC 越大(越接近 1),模型的分类效果越好。
参考资料:https://www.zhihu.com/question/39840928/answer/1085753375
线下AUC提升为什么不能带来线上效果提升?
- 样本
- 线下评测基于历史出现样本,而线上测试存在新样本。因此线下AUC提升可能只是在历史出现样本上有提升,但是对于线上新样本可能并没有效果。
- 数据本身由老模型产生,本身也是存在偏置的。
- 和线下特征不一致。例如包含时间相关特征,存在特征穿越。或者线上部分特征缺失等等。
- 评估目标
- AUC计算的时候,不仅会涉及同一个用户的不同item,也会涉及不同用户的不同item,而线上排序系统每次排序只针对同一个用户的不同item进行打分。
- 线上效果只和用户看到后的点击的可能性有关,和position等偏置因素无关的。而线下一般是不同position的样本混合训练,因此线上和线下评估不对等。
- 分布变化:DNN模型相比传统模型,一般得分分布会更平滑,和传统模型相比打分布不一致。而线上有些出价策略依赖了打分分布,例如有一些相关阈值,那么就可能产生影响。这个可以绘制CTR概率分布图来检查。
参考资料:https://zhuanlan.zhihu.com/p/58152702
特征穿越
对于使用过去以及当下信息来预测未来的AI算法模型,特征穿越本质上是,特征中包含了未来的信息。
对于线上推理过程,构建特征所使用的信息只能来自当下或过去,自然不存在特征穿越问题。
而对于线下训练过程,构建特征时可能会误引入样本发生时刻之后的信息,导致特征穿越。
当训练过程中存在特征穿越问题时,训练评估结果极佳,但线上效果往往会迥然不同。因为模型在训练评估时,使用了特征中的未来信息,而在线上推理时,特征中不再包含未来信息,导致了显著的Training-Serving Skew。
参考资料:https://zhuanlan.zhihu.com/p/402812843