0 前言
- 本文主要讲述了决策树背后的信息熵的公式含义及计算方式,并列举出多道例题帮助理解。
1 信息熵的定义
1.1 信息熵公式

笔者使用下图(1-1)直观理解信息熵的含义。
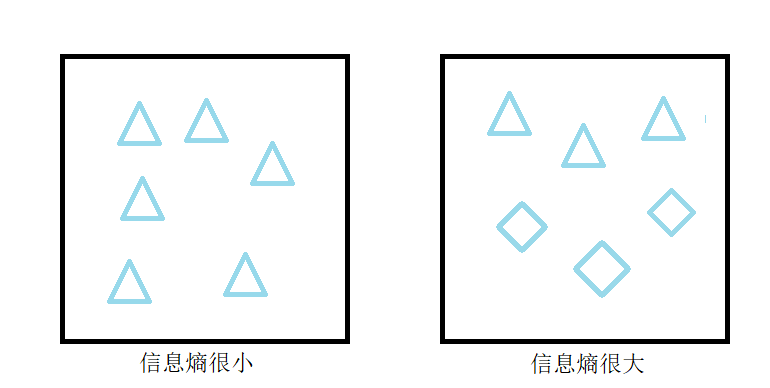
信息熵越大,表示该随机变量的不确定性越高。对于均匀分布,信息熵达到最大值。
1.2 证明:对于均匀分布,信息熵最大
笔者用一个简单的例子加以证明,假如随机变量X只取0和1,即随机变量X服从0 1分布,X的概率密度函数为:
| X | 概率p(0≤p≤1) |
|---|---|
| 1 | p |
| 0 | 1-p |
根据信息熵的公式,随机变量X的信息熵为:
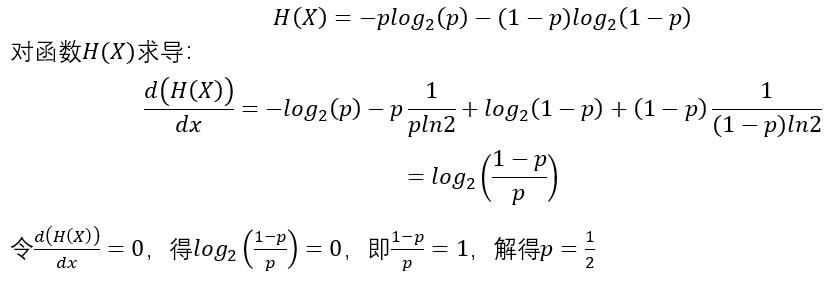
结合下图(1-2),可以看出结论正确。
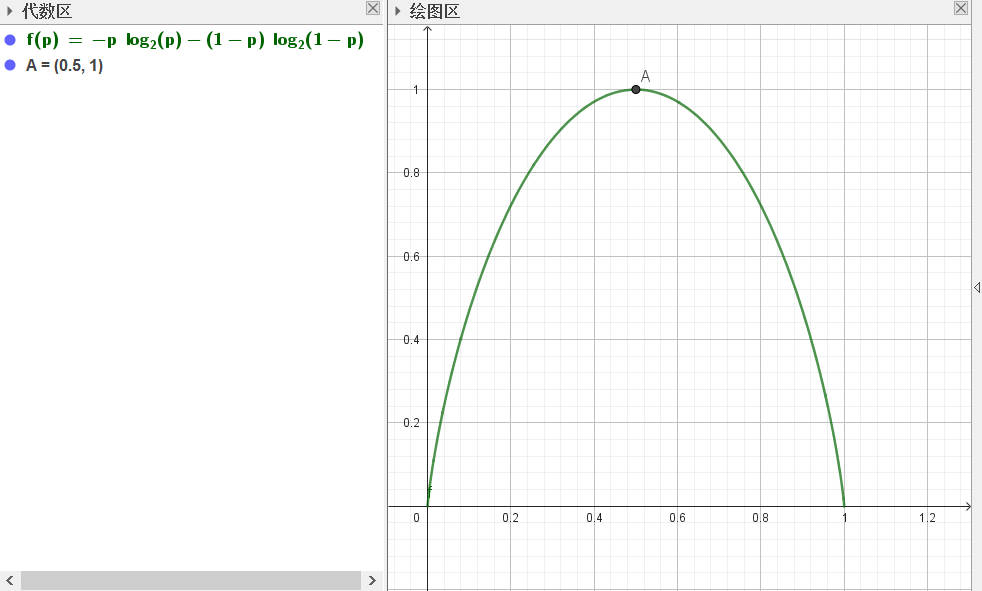
1.3 信息熵公式分析
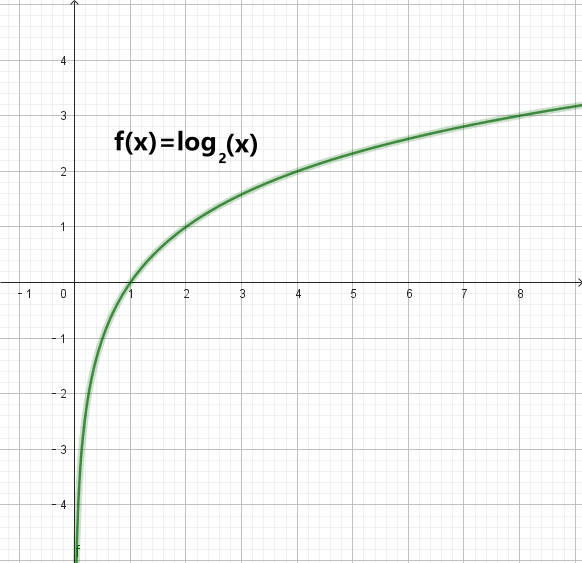
信息熵的计算公式为什么是这样?log函数如下图(1-3)所示,根据概率论,假设某事情p的发生概率>0且<1,即0<p<1,有-∞<log2(p)<0。当出现极端情况,例如p=0或1(p=0或1表示信息很确定,而信息熵是衡量变量不确定性),则根据信息熵公式值为0,log2()函数所得出来的值是负的,需要再添加负号使信息熵变为正值。
2 信息熵的计算
2.1 数据集
假设有以下数据(后文使用该数据集),用于决策是否出去玩。
- 属性id表示每个样本的编号。
- 属性outlook表示户外天气。sunny晴天,overcast阴天,rainy雨天。
- 属性temperature表示温度,hot热,mild温暖,cool冷。
- 属性humidity表示湿度。high高,normal正常。
- 属性windy表示是否有风。not没有,yes有。
- 属性play表示是否出去玩。yes出去玩,no不出去玩。
数据集如下图(2-1)所示。
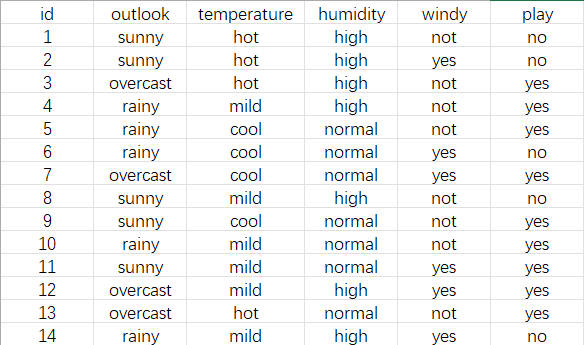
点击查看游玩数据集(CSV格式)
id,outlook,temperature,humidity,windy,play
1,sunny,hot,high,not,no
2,sunny,hot,high,yes,no
3,overcast,hot,high,not,yes
4,rainy,mild,high,not,yes
5,rainy,cool,normal,not,yes
6,rainy,cool,normal,yes,no
7,overcast,cool,normal,yes,yes
8,sunny,mild,high,not,no
9,sunny,cool,normal,not,yes
10,rainy,mild,normal,not,yes
11,sunny,mild,normal,yes,yes
12,overcast,mild,high,yes,yes
13,overcast,hot,normal,not,yes
14,rainy,mild,high,yes,no
2.2 计算变量Play的信息熵
该数据集总样本14个,play变量的取值只能是no或yes。
| 类别 | 个数 | 概率 |
|---|---|---|
| play='no' | 5 | 5/14 |
| play='yes' | 9 | 9/14 |
变量play的信息熵计算如下所示。
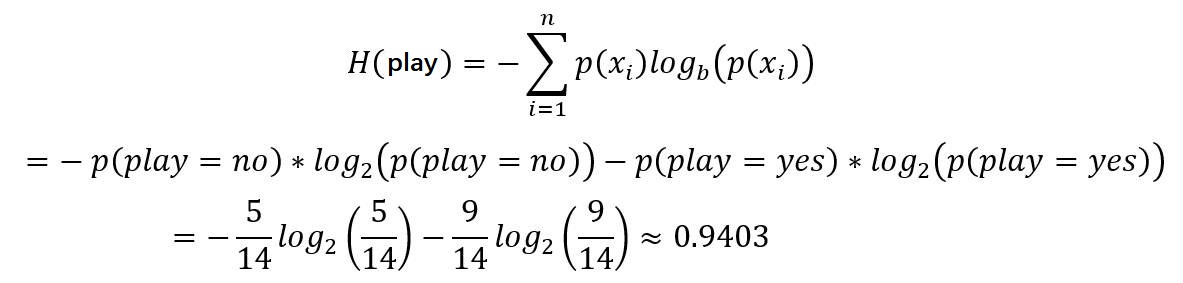
2.3 计算变量Outlook的信息熵
该数据集总样本14个,outlook变量的取值只能是overcast或rainy或sunny。
| 类别 | 个数 | 概率 |
|---|---|---|
| outlook='overcast' | 4 | 4/14 |
| outlook='rainy' | 5 | 5/14 |
| outlook='sunny' | 5 | 5/14 |
变量outlook的信息熵计算如下所示。
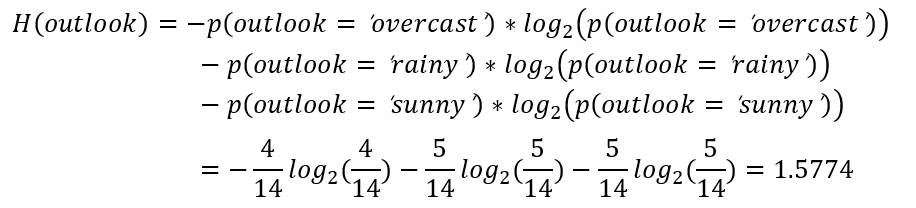
2.3 计算变量Temperature的信息熵
该数据集总样本14个,temperature变量的取值只能是cool或hot或mild。
| 类别 | 个数 | 概率 |
|---|---|---|
| temperature='cool' | 4 | 4/14 |
| temperature='hot' | 4 | 4/14 |
| temperature='mild' | 6 | 6/14 |
变量temperature的信息熵计算如下所示。
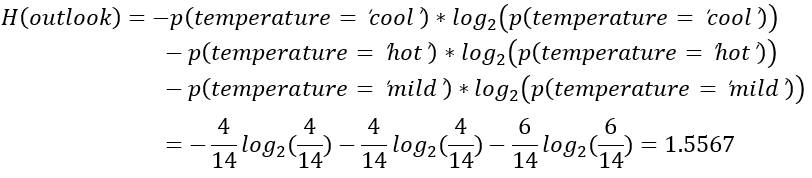
3 信息熵计算程序
稍后补充链接
4 结语
如有错误请指正,禁止商用。