0 前言
- 本文主要介绍决策树条件熵的计算并给出若干例子帮助理解。
- 读者需要具备信息熵计算知识,若不了解请看:信息熵
1 条件熵
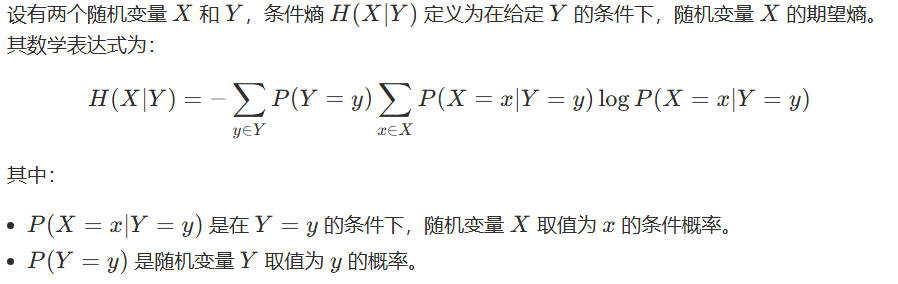
2 数据集
游玩数据集,请看:数据集 1.1节
3 条件熵的计算
使用所给游玩数据集。计算H(play|outlook)的条件熵(在Y随机变量为outlook条件下,X随机变量为play的条件熵)。笔者将Outlook属性排序后如下图(3-1)所示。
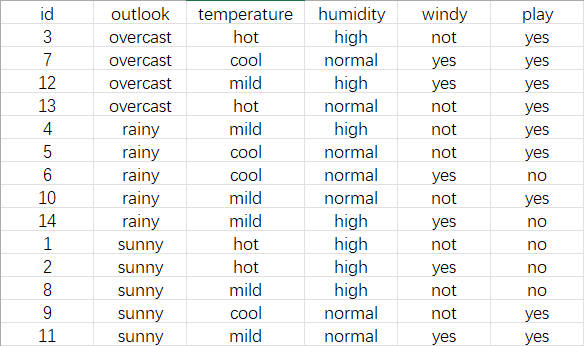
对属性Outlook分析并计算如下。
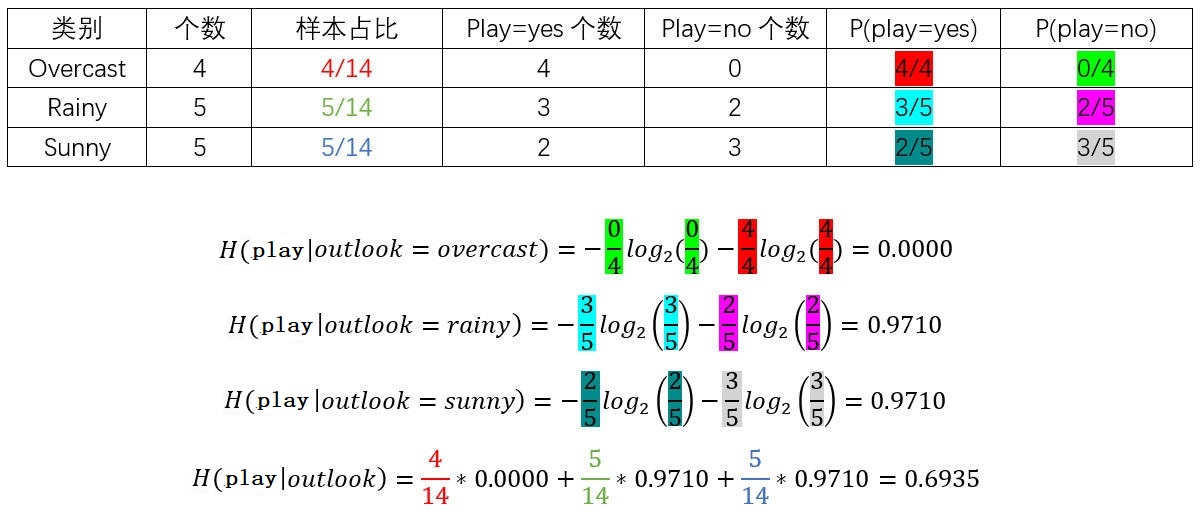
其中相应的运算数据笔者已用相应的颜色标注。属性"Play=yes个数"表示当outlook=overcast条件下的数据中有几个play为yes的样本。属性"P(play=yes)"表示当outlook=overcast条件下play为yes的概率。
同样方法,笔者分别计算随机变量temperature、humidity、windy的条件熵如下所示。
计算temperature条件熵:
-
当temperature=cool时,样本有4个,play=no有1个
当temperature=cool时,样本有4个,play=yes有3个
H(play|temperature=cool)=-(1.0/4.0)log2(1.0/4.0)-(3.0/4.0)log2(3.0/4.0)=0.8113 -
当temperature=hot时,样本有4个,play=no有2个
当temperature=hot时,样本有4个,play=yes有2个
H(play|temperature=hot)=-(2.0/4.0)log2(2.0/4.0)-(2.0/4.0)log2(2.0/4.0)=1.0000 -
当temperature=mild时,样本有6个,play=no有2个
当temperature=mild时,样本有6个,play=yes有4个
H(play|temperature=mild)=-(2.0/6.0)log2(2.0/6.0)-(4.0/6.0)log2(4.0/6.0)=0.9183 -
H(play|temperature)=(4.0/14)* 0.8113+(4.0/14)* 1.0000+(6.0/14)* 0.9183=0.9111
计算humidity条件熵:
-
当humidity=high时,样本有7个,play=no有4个
当humidity=high时,样本有7个,play=yes有3个
H(play|humidity=high)=-(4.0/7.0)log2(4.0/7.0)-(3.0/7.0)log2(3.0/7.0)=0.9852 -
当humidity=normal时,样本有7个,play=no有1个
当humidity=normal时,样本有7个,play=yes有6个
H(play|humidity=normal)=-(1.0/7.0)log2(1.0/7.0)-(6.0/7.0)log2(6.0/7.0)=0.5917 -
H(play|humidity)=(7.0/14)* 0.9852+(7.0/14)* 0.5917=0.7885
计算windy条件熵:
-
当windy=not时,样本有8个,play=no有2个
当windy=not时,样本有8个,play=yes有6个
H(play|windy=not)=-(2.0/8.0)log2(2.0/8.0)-(6.0/8.0)log2(6.0/8.0)=0.8113 -
当windy=yes时,样本有6个,play=no有3个
当windy=yes时,样本有6个,play=yes有3个
H(play|windy=yes)=-(3.0/6.0)log2(3.0/6.0)-(3.0/6.0)log2(3.0/6.0)=1.0000 -
H(play|windy)=(8.0/14)* 0.8113+(6.0/14)* 1.0000=0.8922
4 计算程序
请看:计算程序 2~3节
5 结语
如有错误请指正,禁止商用。