简介
Spearman相关系数,也称为Spearman等级相关系数,是一种非参数的统计度量,用于评估两个变量之间的相关性,即它们是否以某种一致的方式一起变化。与皮尔逊相关系数不同,Spearman相关系数不假设数据是正态分布的,也不要求变量是线性关系。
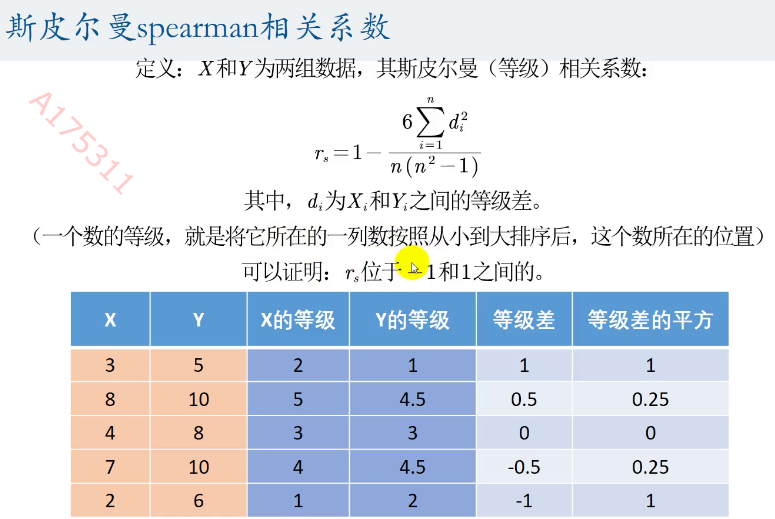
Spearman的检验
在统计学中,p值是在假设检验中用来衡量观测数据与零假设(null hypothesis)之间一致性的指标。
对于计算p值,它是基于样本量和相关系数进行复杂的统计计算得出的,具体计算过程较为复杂,通常通过统计软件或库来实现,难以用简单的公式表达。
直接使用scipy.stats内置的p值计算公式即可
corr, p_value = spearmanr(gdp, life_expectancy)
Spearman与Pearson间的选择
在统计学中,p值是在假设检验中用来衡量观测数据与零假设(null hypothesis)之间一致性的指标。
① 连续,正态分布,线性的数据用pearson相关系数
② 上述任一条件不满足用spearman相关系数
③ 两个定序数据之间用spearman相关系数
运行结果
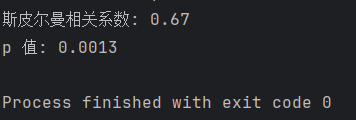
结论
斯皮尔曼相关系数为0.67,表明GDP和人均寿命之间存在中等程度的正相关关系。这意味着随着GDP的增加,人均寿命也倾向于增加,两者之间呈现出一定的正向关联性。p值为0.0013,远小于0.05的显著性水平,表明这种相关性是统计上显著的,我们可以有信心拒绝“GDP和人均寿命之间没有相关性”的零假设。因此,可以认为在所研究的数据集中,GDP的增长与人均寿命的提高之间存在显著的正相关关系。
Full Code
import numpy as np
from scipy.stats import spearmanr# 第一列代表GDP,第二列代表人均寿命
gdp = np.array([62794, 39286, 47603, 42943, 41464, 34483, 46233, 31362, 11289, 8920,9771, 2010, 57305, 30371, 9946, 3894, 52367, 23219, 9370, 82950])
life_expectancy = np.array([78.5, 84.1, 80.8, 80.9, 82.3, 82.8, 81.9, 82.0, 72.4, 75.1,76.4, 68.8, 82.6, 83.1, 75.0, 71.5, 81.6, 74.8, 77.4, 83.3])# 假设 gdp 和 life_expectancy 是已经定义好的两个数值数组
corr, p_value = spearmanr(gdp, life_expectancy)print(f"斯皮尔曼相关系数: {corr:.2f}")
print(f"p 值: {p_value:.4f}")