Python复杂网络社区检测：并行谱聚类算法设计与多种算法应用实战研究

原文链接： https://tecdat.cn/?p=37574

原文出处：拓端数据部落公众号 

 分析师：Leiyun Liao

在当今的网络科学领域，复杂网络中的社区检测成为了一个至关重要的研究课题。随着信息技术的飞速发展，各种大规模网络不断涌现，如社交网络、生物网络等。准确地识别这些网络中的社区结构，对于理解网络的功能、行为以及潜在的规律具有重大意义。

网络社团划分算法作为复杂网络研究的关键内容，一直备受关注。近年来，基于代数图论发展起来的谱聚类算法凭借其利用特征值对应的谱结构来保证划分质量的优势，成为了新的研究热点。然而，在面对大规模网络时，传统的谱聚类算法往往受到时间、内存和 CPU 等资源的限制。为了克服这些限制，将谱聚类算法并行化成为了一种必然的选择。

本文由分析师 Leiyun Liao 深入探讨用于社团探测的并行谱聚类算法设计。同时，通过社区检测算法研究与应用谱聚类、Louvain、irvan-Newman算法和层次迭代谱聚类算法的社交圈社区检测及可视化的数据代码，展示了这些算法在不同网络数据集上的应用和实现过程。通过对这些内容的研究，期望为复杂网络社区检测领域提供有价值的理论和实践参考。

 

用于社团探测的并行谱聚类算法设计

网络社团划分算法是复杂网络中的一个热门话题。近年来，基于代数图论发展的谱聚类算法，利用特征值对应的谱结构，保证了划分质量，是新的研究热点。由于在大规模网络情况下，受到时间、内存、CPU 等限制，需要将谱聚类算法并行化。

任务/目标

采用Python中Multiprocessing模块进行并行设计的方法

并行谱聚类算法的实现

谱聚类算法有3 个重要的步骤：构建Laplacian 矩阵，计算Laplacian 矩阵的前k 个特征向量，实行k-means聚类。谱聚类算法的并行设计就是从上述的3 个方面中有较高时间消耗的步骤进行处理。

 

并行化构建拉普拉斯矩阵

并行化计算特征向量

Lanczos 算法是一种迭代算法，用于计算n 阶埃尔米特矩阵的m(m ⩽ n)个“最有用的”的特征值与特征向量，符合求解Laplacian矩阵前k个特征值和特征向量的需求。并行计算特征向量主要是针对Lanczos算法中主要的消耗时间的操作——矩阵L与向量v_j的乘积运算。设计想法为：将矩阵L进行行分块，分配到不同CPU 上计算与向量v_j的乘积，最后将计算结果合并为向量。

并行化k-means聚类

k-means聚类是一个迭代过程。每次迭代分为两步：首先，找到每个点离它最近的中心点并归入该类；其次，重新计算中心点。重复上述两部，直到收敛。本文采用的收敛准则是前后两次聚类结果一致。由于新的中心点会被用于下一步迭代，且在每次迭代中必须更新，因此迭代过程无法并行。但是，计算不同点和各个中心的距离和其所属类是可以并行的。

 

为了对上述设计的并行谱聚类算法进行测试，我们采用三组数据进行测试分析。本文中用来测试的数据为社团结构探测算法常用的经典数据，使用实际网络Zachary空手道俱乐部成员关系网，2000年美国大学生美式足球赛网络和Polblog网络来测试算法的划分质量，使用LFG基准网络调节网络大小来测试算法运行时间。本文测试所用的环境全部为Intel(R) Core(TM) i7 10510U CPU @ 1.80GHz，8.00GB 内存，Windows10 操作系统。社团划分质量通过Newman 等人提出的模块度来衡量，

Zachary空手道俱乐部

选定高斯函数中的参数σ = 5，k 近邻算法中参数k = 5，利用3.2 节所介绍的算法对该网络进行处理，并利用模块度对社团划分的质量进行评价。模块度Q 与社团个数k 的变化情况如图9所示。由图可以得出：模块度Q 最大对应的社团个数为2，恰为实际的社团个数。

当社团个数为2 时，得到的具体划分结果见图10。经多次实验发现，节点8 会被错分，其余节点都被正确划分到相应的社团中。因此，该算法用于空手道俱乐部网络社团划分的效果较好。

2000年美式足球赛网络

选定高斯函数中的参数σ = 5，k 近邻算法中参数k = 5，利用3.2 节所介绍的算法对该网络进行处理。模块度Q 与社团个数k 的变化情况如图11所示。模块度Q 最大值为0.602，对应的社团个数为11。与实际的12 个联盟有误差，但两者模块度相差不大。

PolBlogs 网络

选定高斯函数中的参数σ = 5，k 近邻算法中参数k = 5。模块度Q 与社团个数k 的变化情况如图12所示。模块度Q 最大值为0.229，对应的社团个数为3，与实际的2 个政治派别有误差。

算法运行时间

LFR 基准网络是测试社团划分算法的经典人工网络，网络中的度分布和社团大小均服从幂律分布。我们通过调节LFR 网络的规模n 来测试并行算法的运行时间，其余参数为γ = 3, ζ = 1.8, μ = 0.1，结果见表3。

结果讨论与分析

在计算相同数据规模的情况下，发现本文用Python 中Multiprocessing 模块设计的并行算法运行时间比使用Hadoop并行框架的慢很多。考虑原因可能是：

1) 开设进程和多进程间的来回切换也是需要开销的。算法实现中涉及到了Lanczos算法和kmeans算法等都是迭代算法，每次迭代过程中频繁的进程切换会消耗时间。这一点也应证了计算特征向量时的高时间消耗；

2) 由于进程间的数据并不能共享，每次创建一个进程都需要拷贝主进程中的数据和传入数据，数据量增大的同时，拷贝、传入也需要消耗额外时间；

3) 能同时进行计算的CPU 数量会受到电脑配置的影响，且时间复杂度从理论上说是单进程的1/p（p 为CPU 个数）。就拿笔记本电脑来说，理论上最多只能缩短1/4 或1/8，何况还要考虑其他开销带来的损失。

针对以上问题，后续需对程序进行优化，优化的主要方向有：

1. 优化数据存储方式，减少进程间数据共享带来的消耗；
2. 替换高时间消耗的算法，如可以利用用kd 树技术进行矩阵稀疏化；

3) 借鉴Hadoop 中的MapReduce 并行计算模型，用Python 语言实现，提高效率。 

 

社区检测算法研究与应用谱聚类、Louvain、irvan-Newman算法|附数据代码

社区检测，又称为社区搜索，其本质是在图结构中寻找那些彼此紧密连接且在结构上相互趋近的节点集合。在本研究中所涉及的社区检测库，采用了三种重要的算法来实现这一目标。

（一）谱聚类
谱聚类算法通过对图的拉普拉斯矩阵进行特征分解，将图中的节点划分到不同的社区中。该算法在处理复杂的图结构时具有较高的准确性和稳定性。

（二）Louvain 方法
Louvain 方法是一种基于模块度优化的社区检测算法。它通过不断地合并节点，使得整个图的模块度不断提高，从而得到最终的社区划分。

（三）Girvan-Newman 算法
Girvan-Newman 算法通过逐步移除图中的边，来识别图中的社区结构。该算法基于边介数的概念，能够有效地发现图中的层次社区结构。

应用

我们在植入 L 分区模型（代码内有详细规范说明）以及扎卡里空手道俱乐部网络上对本库进行了测试，以实现结果的可视化呈现。

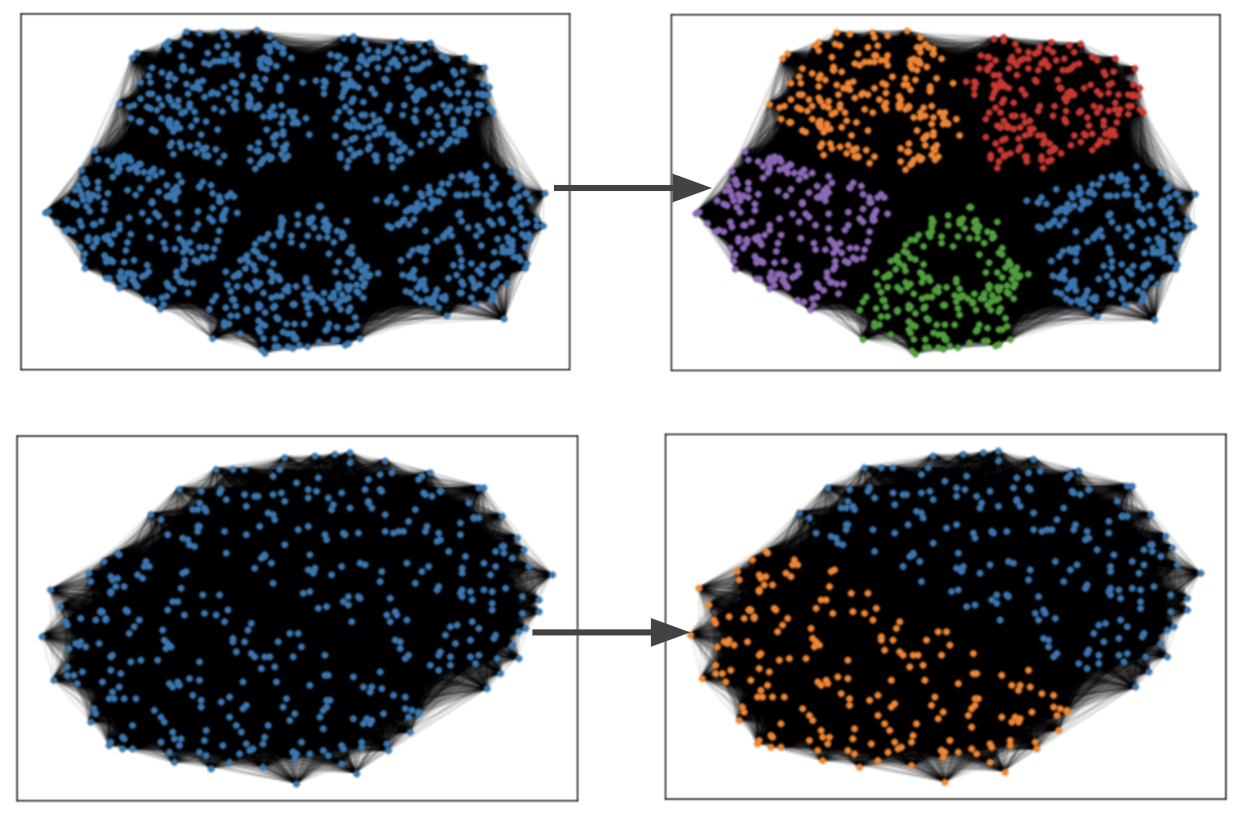
空手道俱乐部网络

 

算法及用法

（一）谱聚类

在植入 L 分区模型上进行测试：

1.  
   labels_dict = spectral_clustering(G_pl,
2.  
   K,
3.  
   pos_pl,
4.  
   COLORS,
5.  
   laplacian_type="symmetric",
6.  
   edge_alpha=0.1,
7.  
   node_size=10,
8.  
   labels=False)

俱乐部网络上进行测试：

1.  
   G_kk = nx.karate_club_graph()
2.  
   pos_kk = nx.spring_layout(G_kk)
3.  
    
4.  
   visualize_graph(G_kk, pos_kk)

Louvain 方法

在植入 L 分区模型上进行测试：

1.  
   result = plantedl()
2.  
    
3.  
   G = result[0]
4.  
   pos = nx.spring_layout(G)
5.  
    
6.  
   final_partition = result[1][0]

Girvan-Newman

你同样可以使用原始的 Networkx 可视化选项来呈现这些算法所产生的结果。

在植入 L 分区模型上进行测试：

1.  
    
2.  
   G = nx.planted_partition_graph(5, 30, 0.8, 0.1)
3.  
   pos = nx.spring_layout(G, k=0.1, iterations=30, scale=1.3)

 

层次迭代谱聚类算法的社交圈社区检测及可视化|附数据代码

 本研究旨在对 Facebook 的 “Social Circles Dataset” 进行社区检测，并通过绘制图形实现可视化。该数据集对应的图是无向、无权的，包含 4039 个节点和 88234 条边。我们采用了层次迭代谱聚类算法，利用菲德勒向量进行社区检测。本文详细介绍了该算法的实现过程及相关的绘图函数。

一、研究目标

对 社交圈数据进行社区检测，并通过绘制图形实现可视化。

二、算法描述

层次迭代谱聚类算法

1. 谱分解：单次迭代

   函数spectralDecomp_OneIter(nodes_connectivity_list)用于实现谱分解的单次迭代。该函数首先获取节点列表，计算节点数量，创建节点到索引的映射以及索引到节点的映射。接着创建邻接矩阵和度矩阵。

1.  
    
2.  
   node_to_idx, idx_to_node = get_nodes_mapping(nodes)
3.  
    
4.  
   adj_matrix = get_adj_matrix(nodes_connectivity_list,node_to_idx,num_nodes)
5.  
    
6.  
   degree_matrix = np.zeros((num_nodes,num_nodes),dtype=int)
7.  
   for node,row in enumerate(adj_matrix):
8.  
   degree_matrix[node][node] = np.sum(row)

1. 谱分解：多次迭代

   函数spectralDecomposition(nodes_connectivity_list)实现了多次迭代的谱分解。在每次迭代中，从队列中取出子图进行单次迭代的谱分解，得到菲德勒向量、邻接矩阵和图分区。通过分析图分区中的社区，确定是否需要进一步迭代。

1.  
    
2.  
   num_nodes = len(nodes)
3.  
    
4.  
   node_to_idx, idx_to_node = get_nodes_mapping(nodes)
5.  
    
6.  
   queue = []
7.  
   final_clusters = np.empty((num_nodes,2),dtype=int)
8.  
   iter = 0
9.  
   unique_clusters = 0
10.  
    min_cluster_size = 20
11.  
    queue.append(nodes_connectivity_list)
12.  
    while queue:
13.  
    subgraph = queue.pop(0)
14.  
    fielder_vec_fb,adj_matrix_fb, graph_partition_fb = spectralDecomp_OneIter(subgraph)
15.  
    communities = [label for _,label in graph_partition_fb]
16.  
    community_ids = np.unique(communities)

 

创建排序邻接矩阵

函数createSortedAdjMat(partition, edge_list)根据图分区和边列表创建排序后的邻接矩阵。该函数首先从边列表中获取唯一的节点名称，建立节点名称与索引的映射关系。然后计算节点数量，创建空的邻接矩阵，并根据边列表填充矩阵元素。

1.  
   nodes = np.unique(edge_list)
2.  
   name_to_index = {}
3.  
   index_to_name = {}
4.  
   for index, name in enumerate(nodes):
5.  
   name_to_index[name] = index
6.  
   index_to_name[index] = name

 

绘图函数

用于绘制排序后的邻接矩阵图像，并保存为文件。 

算法实现步骤

1. 首先，对数据集进行谱分解的多次迭代，得到图分区。
2. 然后，根据图分区和边列表创建排序后的邻接矩阵。
3. 接着，使用绘图函数分别绘制排序后的邻接矩阵、菲德勒向量和社区可视化图像。

 

1.  
   print('Plotting Sorted Adjacency Matrix:')
2.  
   plt.imshow(sorted_adj_matrix,cmap='inferno_r')
3.  
   plt.title(plot_title)
4.  
   plt.show()
5.  
   plt.savefig('../plots/spectral_adj_matrix.png')
6.  
    
7.  
   print('Visualizing Communities')
8.  
   nodes = []

 

 

1.  
   sorted_adj_matrix = createSortedAdjMat(graph_partition_fb,nodes_connectivity_list_fb)
2.  
   plot_sorted_adjMatrix(sorted_adj_matrix,p

 

 

 

plot_graph(graph_partition_fb,nodes_connectivity_list

 

 

关于分析师 

 

在此对Leiyun Liao对本文所作的贡献表示诚挚感谢，他在上海大学完成了数学与应用数学专业的学位，专注统计学习模型领域。擅长 Python。