【题目全解】蓝桥杯24省赛C++中高级组题干题解

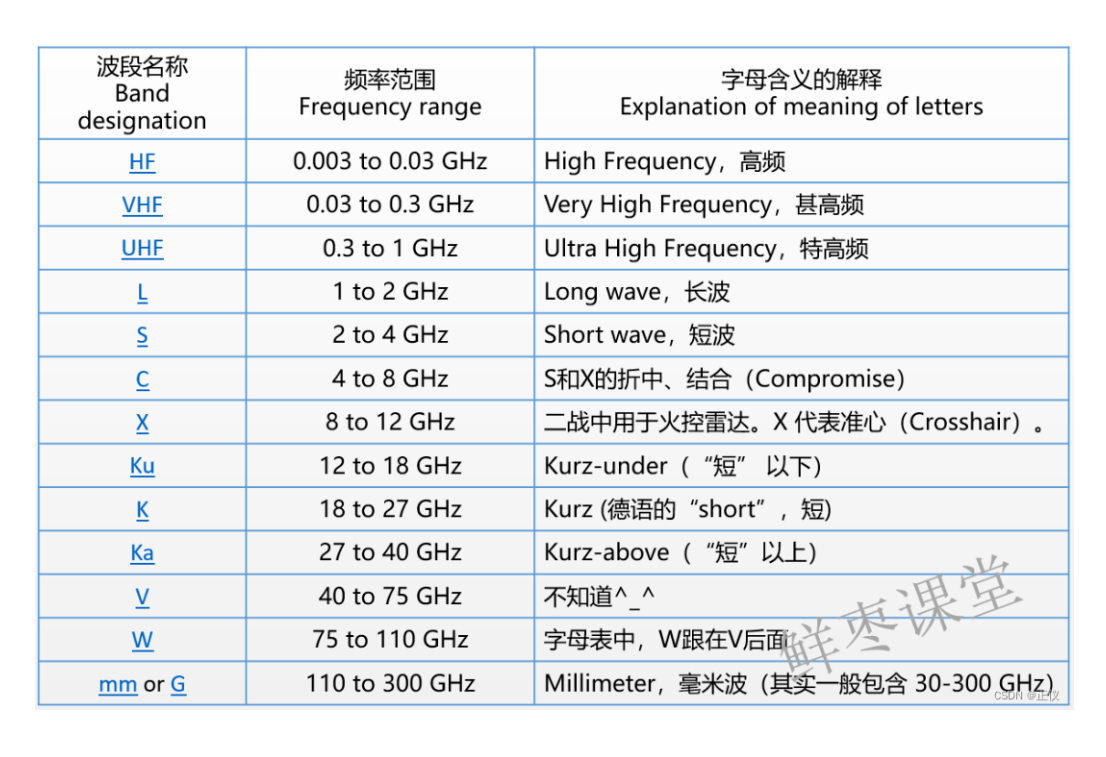
本帖只提供六道编程题的解题思路，部分题目并不提供实际的代码（因为我赛时忘记把代码截图下来了）。

T1 - 看书

题干描述： 一本书共 \(n\) 页，小明计划第一天看 \(x\) 页，此后每一天都要比前一天多看 \(y\)
页，请问小明几天可以看完这本书？

输入格式： 一行输入三个整数 \(n\)，\(x\)，\(y\) \((20\le n\le 5000，1\le x，y\le 20)\)，分别表示书的总页数、计划第一天看的页数以及此后每天都要比前一天多看的页数，整数之间以一个空格隔开。

输出格式： 输出一个整数，表示小明几天可以看完这本书。

样例输入：100 10 5

样例输出：5

解题思路： 防爆零题。用一个 while 循环来判断还有多少页的书需要看，循环里拿一个变量来记录循环次数作为答案即可。

T2 - 数字交换

题干描述： 给定一个正整数 \(n\)，请将 \(n\) 的最高位与最低位的数字进行交换，并输出交换后的结果。如果交换后的结果有前导 \(0\)，去除前导 \(0\) 后再输出结果。

输入描述： 输入一个正整数 \(n (100\le n\le10^9)\)。

输出描述： 输出答案。

样例输入： 173

样例输出： 371

解题思路： 以字符串的形式来读入字符，先用 C++ 自带的 swap 交换该字符串的第一位和最后一位。之后用 while 循环记录第一个合法数字出现的位置（即删除前导零）。最后用 string 类的 .substr() 方法截取字符串有效子串。

T3 - 出现奇数次的数

题干描述： 给定 \(n\) 个整数，其中只有一个数出现了奇数次，请找出这个数。

输入格式：

第一行输入一个整数 \(n (1\le n \le 10^5)\)。
第二行输入 \(n\) 个整数 \((1\le 整数\le 10^9)\)，整数之间以一个空格隔开（数据保证只有一个数出现了奇数次）

输出格式： 输出一个整数，表示出现了奇数次的数。

样例输入：

7
6 2 4 6 4 2 6

样例输出：

6

解题思路：

这道题可以有多种算法来解。一种方法是使用 sort 函数对数组排序，然后找出某个出现奇数次的数即可。还可以用 STL 的 map 数据结构，类似桶排序的方法，来记录某一个键出现的次数，最后扫一遍就可以找出来了。

最方便的做法是使用异或的性质来快速找到某个出现奇数次的数。具体地，将数组中的所有元素依次进行异或运算，最终结果就是唯一一个出现奇数次的数，因为出现偶数次的数都会在异或中抵消掉。

代码展示：

#include <iostream>
using namespace std;int main(){int n, t, ans = 0;cin >> n; while(n--){cin >> t;ans ^= t;}cout << ans << endl;return 0;
}

T4 - 字母移位

这道题是我觉得整一场比赛中最有问题的题目了。开了 long long 过不了，不开 long long 不取模竟然是过得了的。这证明这道题的数据是有问题的。（一个半小时的考试，这道题浪费了我一个小时的调试时间。我只能说，出题组太垃圾了）。

题干描述：

字母移位：表示将字母按照字母表的顺序进行移动。

例如：'b' 向右移动一位是 'c'，“向左移动两位是 'd'。

特别地，'a' 向左移动一位是 'z'，'z' 向右移动一位是 'a'。

给定一个仅包含小写字母且长度为 \(n\) 的字符串 \(s\)，以及 \(n\) 个正整数 \(a_1, a_2, \dots, a_n\)，接下来对字符串 \(s\) 按如下规律操作：

1. 将第 \(1\) 位字符向左移动 \(a_1\) 位；
2. 再将第 \(1、2\) 位字符都向右移动 \(a_2\) 位；
3. 再将第 \(1、2、3\) 位字符都向左移动 \(a_3\) 位；
4. 再将第 \(1、2、3、4\) 位字符都向右移动 \(a_4\) 位；

以此类推，直到将 \(s\) 的第 \(1\) 到第 \(n\) 位字符都（按规律向左或向右）移动完毕。

最后，将操作完成后的字符串 \(s\) 输出。

例如：\(n = 5\)，字符串 s = "abcde"，\(5\) 个正整数为 1, 3, 5, 7, 9；

将 "abcde" 的第 \(1\) 位字符 "a" 向左移动 \(1\) 位，\(s\) 变为 "zbcde"；

再将 "zbcde" 的前 \(2\) 位字符 "zb" 向右移动 \(3\) 位，\(s\) 变为 "cecde"；

再将 "cecde" 的前 \(3\) 位字符 "cec" 向左移动 \(5\) 位，\(s\) 变为 "xzxde"；

再将 "xzxde" 的前 \(4\) 位字符 "xzxd" 向右移动 \(7\) 位，\(s\) 变为 "egeke"；

再将 "egeke" 的前 \(5\) 位字符 "egeke" 向左移动 \(9\) 位，\(s\) 变为 "vxvbv"。

最后，将操作完成后的字符串 "vxvbv" 输出。

样例输入：

5
abcde
1 3 5 7 9

样例输出：

vxvbv

解题思路：

首先看数据量，发现这道题的数据量特别大，如果暴力的话肯定是会 TLE 的（亲测，暴力可以拿到 \(36\%\) 的高分。考虑按照以下方法优化：

注意到对于字符串的第 i 个字符，在完全模拟的过程中会调整 \(n - i + 1\) 次。但事实上，我们只需要记录某一个字符最终的偏移量就好了。参考样例，a 字符在经过 -1, +3, -5, +7, -9 （ASCII 码位移）后，最终只会偏移 -5 位。我们只需要记录每一位的最终偏移量就好了。

为了优化算法，考虑使用差分的策略来进行区间位移的操作。具体代码如下（整解，但因数据问题无法 AC）：

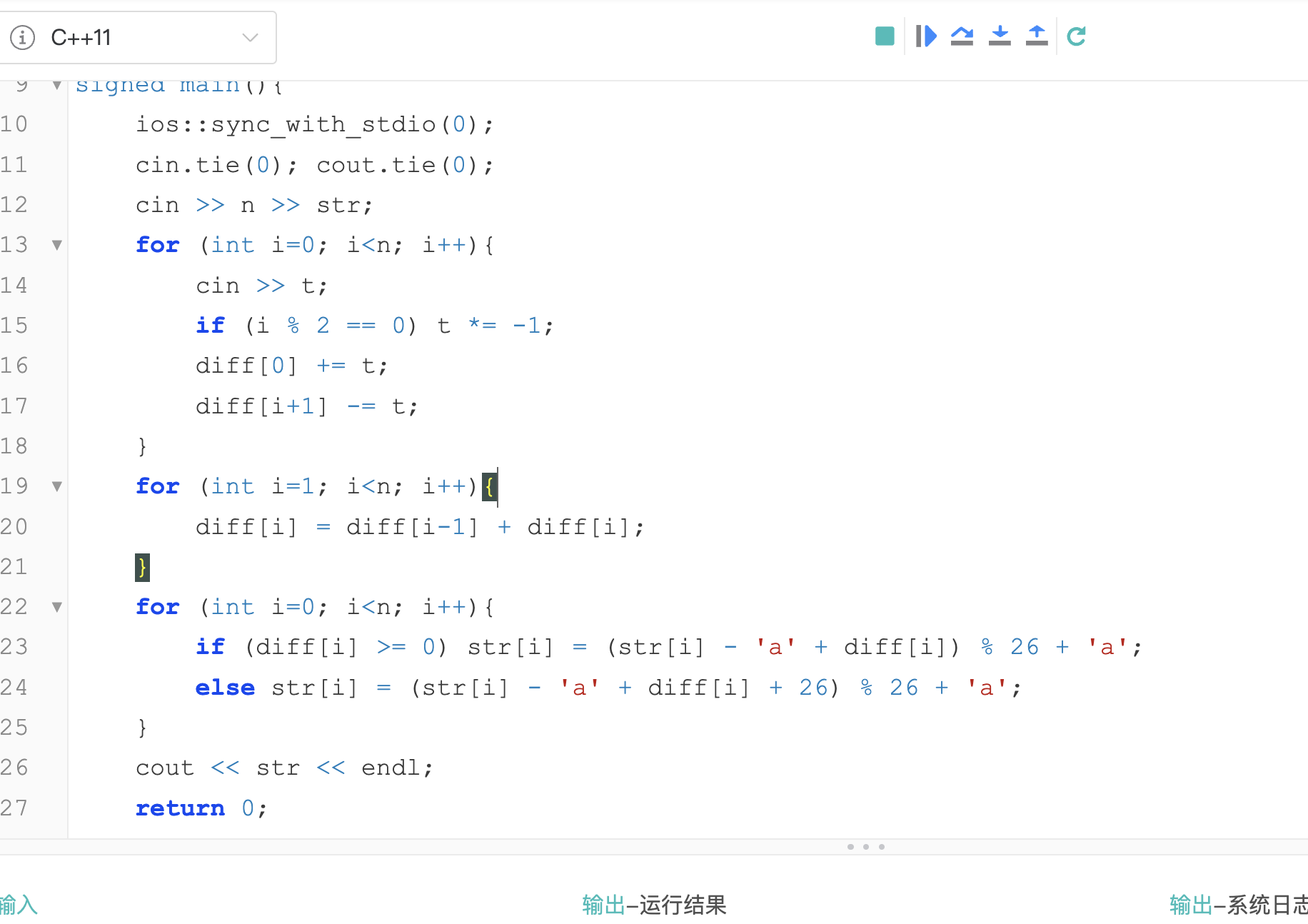
备注：记得开 int，开 long long 不拿分。

T5 - 通关游戏的最少能量值。

题干描述：

有一款新游戏，通关这个游戏需要完成 \(n\) 个任务，这 \(n\) 个任务可按任意次序完成。每个任务设置了启动能量值和完成任务消耗的能量值，且消耗的能量值小于等于该任务的启动能量值。如果玩家当前的能量值低于该任务启动能量值，则不能开始该任务。

例 1：玩家当前的能量值为 \(7\)，当前任务的启动能量值为 \(5\)，完成任务消耗的能量值为 \(3\)，则可以开始该任务，完成任务后玩家剩余能量值为 \(4\)；

例 2：玩家当前的能量值为 \(5\)，当前任务的启动能量值为 \(8\)，则无法开始该任务。

游戏开始时玩家需要一个初始能量值用来完成这 \(n\) 个任务。当给定每个任务的启动能量值和完成任务消耗的能量值时，请问初始能量的最小值是多少？

样例输入：

3
2 2
9 5
7 4

样例输出：

12

解题思路： 考虑使用二分+贪心的策略。首先用贪心算法求得一个最优的打怪顺序。在这里，我们可以按照打完怪兽的剩余血量对数组进行排序。之后二分答案判断以 mid 为初始血量是否可以打完所有的怪物即可。

T6 - 物品分组

巧了，洛谷原题。我在 \(N\) 年前做过这道题目。链接：P1182 数列分段

数列分段 Section II

题目描述

题干描述： 对于给定的一个长度为 \(N\) 的正整数数列 \(A_{1\sim N}\)，现要将其分成 \(M\)（\(M\leq N\)）段，并要求每段连续，且每段和的最大值最小。

样例输入：

5 2
6 1 3 8 4

样例输出：

12

解题思路： 也是一道很经典的二分答案题目，二分判断当每一段的和最大为 mid 时，是否可以分成 \(m\) 段即可。check 函数也是比较好写的。

#include <iostream>
#include <algorithm>
using namespace std;int n, m;
int l, r, ans;
int arr[100005];// 判断当每一段的和最大为 mid 时，是否可以分成 m 段。
bool check(int mid){int cut=1, current=0;for (int i=0; i<n; i++){if (current + arr[i] <= mid){current += arr[i];} else{current = arr[i];cut++;}}return cut <= m;
}int main(){cin >> n >> m;int total=0;for (int i=0; i<n; i++){cin >> arr[i];r += arr[i];l = max(l, arr[i]);}while(l <= r){int mid = (l+r)/2; if(check(mid)){r = mid - 1;ans = mid;} else l = mid + 1;}cout << l << endl;return 0;
}

本帖只提供六道编程题的解题思路，部分题目并不提供实际的代码（因为我赛时忘记把代码截图下来了）。

T1 - 看书

题干描述： 一本书共 \(n\) 页，小明计划第一天看 \(x\) 页，此后每一天都要比前一天多看 \(y\)
页，请问小明几天可以看完这本书？

输入格式： 一行输入三个整数 \(n\)，\(x\)，\(y\) \((20\le n\le 5000，1\le x，y\le 20)\)，分别表示书的总页数、计划第一天看的页数以及此后每天都要比前一天多看的页数，整数之间以一个空格隔开。

输出格式： 输出一个整数，表示小明几天可以看完这本书。

样例输入：100 10 5

样例输出：5

解题思路： 防爆零题。用一个 while 循环来判断还有多少页的书需要看，循环里拿一个变量来记录循环次数作为答案即可。

T2 - 数字交换

题干描述： 给定一个正整数 \(n\)，请将 \(n\) 的最高位与最低位的数字进行交换，并输出交换后的结果。如果交换后的结果有前导 \(0\)，去除前导 \(0\) 后再输出结果。

输入描述： 输入一个正整数 \(n (100\le n\le10^9)\)。

输出描述： 输出答案。

样例输入： 173

样例输出： 371

解题思路： 以字符串的形式来读入字符，先用 C++ 自带的 swap 交换该字符串的第一位和最后一位。之后用 while 循环记录第一个合法数字出现的位置（即删除前导零）。最后用 string 类的 .substr() 方法截取字符串有效子串。

T3 - 出现奇数次的数

题干描述： 给定 \(n\) 个整数，其中只有一个数出现了奇数次，请找出这个数。

输入格式：

第一行输入一个整数 \(n (1\le n \le 10^5)\)。
第二行输入 \(n\) 个整数 \((1\le 整数\le 10^9)\)，整数之间以一个空格隔开（数据保证只有一个数出现了奇数次）

输出格式： 输出一个整数，表示出现了奇数次的数。

样例输入：

7
6 2 4 6 4 2 6

样例输出：

6

解题思路：

这道题可以有多种算法来解。一种方法是使用 sort 函数对数组排序，然后找出某个出现奇数次的数即可。还可以用 STL 的 map 数据结构，类似桶排序的方法，来记录某一个键出现的次数，最后扫一遍就可以找出来了。

最方便的做法是使用异或的性质来快速找到某个出现奇数次的数。具体地，将数组中的所有元素依次进行异或运算，最终结果就是唯一一个出现奇数次的数，因为出现偶数次的数都会在异或中抵消掉。

代码展示：

#include <iostream>
using namespace std;int main(){int n, t, ans = 0;cin >> n; while(n--){cin >> t;ans ^= t;}cout << ans << endl;return 0;
}

T4 - 字母移位

这道题是我觉得整一场比赛中最有问题的题目了。开了 long long 过不了，不开 long long 不取模竟然是过得了的。这证明这道题的数据是有问题的。（一个半小时的考试，这道题浪费了我一个小时的调试时间。我只能说，出题组太垃圾了）。

题干描述：

字母移位：表示将字母按照字母表的顺序进行移动。

例如：'b' 向右移动一位是 'c'，“向左移动两位是 'd'。

特别地，'a' 向左移动一位是 'z'，'z' 向右移动一位是 'a'。

给定一个仅包含小写字母且长度为 \(n\) 的字符串 \(s\)，以及 \(n\) 个正整数 \(a_1, a_2, \dots, a_n\)，接下来对字符串 \(s\) 按如下规律操作：

1. 将第 \(1\) 位字符向左移动 \(a_1\) 位；
2. 再将第 \(1、2\) 位字符都向右移动 \(a_2\) 位；
3. 再将第 \(1、2、3\) 位字符都向左移动 \(a_3\) 位；
4. 再将第 \(1、2、3、4\) 位字符都向右移动 \(a_4\) 位；

以此类推，直到将 \(s\) 的第 \(1\) 到第 \(n\) 位字符都（按规律向左或向右）移动完毕。

最后，将操作完成后的字符串 \(s\) 输出。

例如：\(n = 5\)，字符串 s = "abcde"，\(5\) 个正整数为 1, 3, 5, 7, 9；

将 "abcde" 的第 \(1\) 位字符 "a" 向左移动 \(1\) 位，\(s\) 变为 "zbcde"；

再将 "zbcde" 的前 \(2\) 位字符 "zb" 向右移动 \(3\) 位，\(s\) 变为 "cecde"；

再将 "cecde" 的前 \(3\) 位字符 "cec" 向左移动 \(5\) 位，\(s\) 变为 "xzxde"；

再将 "xzxde" 的前 \(4\) 位字符 "xzxd" 向右移动 \(7\) 位，\(s\) 变为 "egeke"；

再将 "egeke" 的前 \(5\) 位字符 "egeke" 向左移动 \(9\) 位，\(s\) 变为 "vxvbv"。

最后，将操作完成后的字符串 "vxvbv" 输出。

样例输入：

5
abcde
1 3 5 7 9

样例输出：

vxvbv

解题思路：

首先看数据量，发现这道题的数据量特别大，如果暴力的话肯定是会 TLE 的（亲测，暴力可以拿到 \(36\%\) 的高分。考虑按照以下方法优化：

注意到对于字符串的第 i 个字符，在完全模拟的过程中会调整 \(n - i + 1\) 次。但事实上，我们只需要记录某一个字符最终的偏移量就好了。参考样例，a 字符在经过 -1, +3, -5, +7, -9 （ASCII 码位移）后，最终只会偏移 -5 位。我们只需要记录每一位的最终偏移量就好了。

为了优化算法，考虑使用差分的策略来进行区间位移的操作。具体代码如下（整解，但因数据问题无法 AC）：

备注：记得开 int，开 long long 不拿分。

T5 - 通关游戏的最少能量值。

题干描述：

有一款新游戏，通关这个游戏需要完成 \(n\) 个任务，这 \(n\) 个任务可按任意次序完成。每个任务设置了启动能量值和完成任务消耗的能量值，且消耗的能量值小于等于该任务的启动能量值。如果玩家当前的能量值低于该任务启动能量值，则不能开始该任务。

例 1：玩家当前的能量值为 \(7\)，当前任务的启动能量值为 \(5\)，完成任务消耗的能量值为 \(3\)，则可以开始该任务，完成任务后玩家剩余能量值为 \(4\)；

例 2：玩家当前的能量值为 \(5\)，当前任务的启动能量值为 \(8\)，则无法开始该任务。

游戏开始时玩家需要一个初始能量值用来完成这 \(n\) 个任务。当给定每个任务的启动能量值和完成任务消耗的能量值时，请问初始能量的最小值是多少？

样例输入：

3
2 2
9 5
7 4

样例输出：

12

解题思路： 考虑使用二分+贪心的策略。首先用贪心算法求得一个最优的打怪顺序。在这里，我们可以按照打完怪兽的剩余血量对数组进行排序。之后二分答案判断以 mid 为初始血量是否可以打完所有的怪物即可。

T6 - 物品分组

巧了，洛谷原题。我在 \(N\) 年前做过这道题目。链接：P1182 数列分段

数列分段 Section II

题目描述

题干描述： 对于给定的一个长度为 \(N\) 的正整数数列 \(A_{1\sim N}\)，现要将其分成 \(M\)（\(M\leq N\)）段，并要求每段连续，且每段和的最大值最小。

样例输入：

5 2
6 1 3 8 4

样例输出：

12

解题思路： 也是一道很经典的二分答案题目，二分判断当每一段的和最大为 mid 时，是否可以分成 \(m\) 段即可。check 函数也是比较好写的。

#include <iostream>
#include <algorithm>
using namespace std;int n, m;
int l, r, ans;
int arr[100005];// 判断当每一段的和最大为 mid 时，是否可以分成 m 段。
bool check(int mid){int cut=1, current=0;for (int i=0; i<n; i++){if (current + arr[i] <= mid){current += arr[i];} else{current = arr[i];cut++;}}return cut <= m;
}int main(){cin >> n >> m;int total=0;for (int i=0; i<n; i++){cin >> arr[i];r += arr[i];l = max(l, arr[i]);}while(l <= r){int mid = (l+r)/2; if(check(mid)){r = mid - 1;ans = mid;} else l = mid + 1;}cout << l << endl;return 0;
}