1.课题概述
基于迭代扩展卡尔曼滤波算法的倒立摆控制系统,对比UKF,EKF迭代UKF,迭代EKF四种卡尔曼滤波的控制效果。
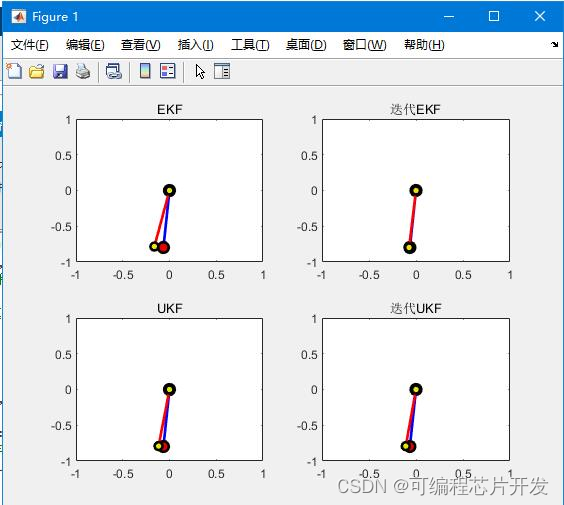
2.系统仿真结果
3.核心程序与模型
版本:MATLAB2022a
%迭代扩展卡尔曼滤波
X_iukf = zeros(2, Times1);
X_iukf(:,1) = state0;
P_iukf = zeros(2,2,Times1);
P_iukf(:,:,1) = Sigma_;
for i=1:Times1-1[X_iukf(:,i+1), P_iukf(:,:,i+1)] = func_iter_EKF(X_iukf(:,i), P_iukf(:,:,i), f, [z_(i,:)]', Q, R, dt);
end
err_ekf =X_ekf - theta00(1:dt/dt0:end,:)';
err_iekf = X_iekf - theta00(1:dt/dt0:end,:)';
err_ukf =X_ukf - theta00(1:dt/dt0:end,:)';
err_iukf = X_iukf - theta00(1:dt/dt0:end,:)';figure
subplot(2,2,1)
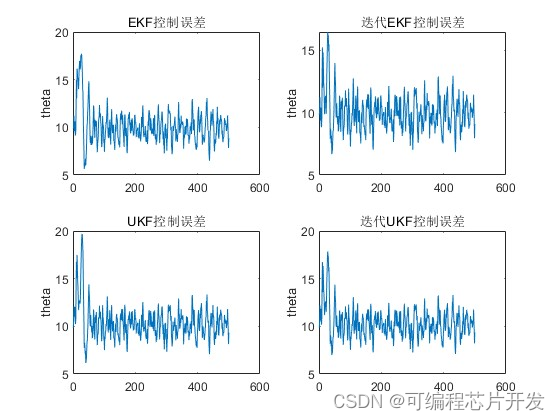
plot(mod(err_ekf(1,:)-pi, 2*pi).^2)
title('EKF控制误差')
ylabel('theta');
subplot(2,2,2)
plot(mod(err_iekf(1,:)-pi,2*pi).^2)
title('迭代EKF控制误差')
ylabel('theta');
subplot(2,2,3)
plot(mod(err_ukf(1,:)-pi,2*pi).^2)
title('UKF控制误差')
ylabel('theta');
subplot(2,2,4)
plot(mod(err_iukf(1,:)-pi,2*pi).^2)
title('迭代UKF控制误差')
ylabel('theta');figure
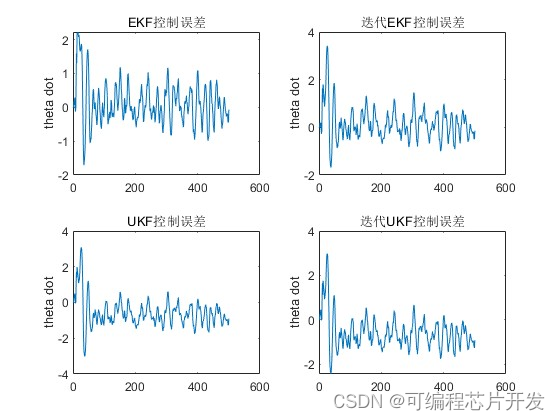
subplot(2,2,1)
plot(err_ekf(2,:))
title('EKF控制误差')
ylabel('theta dot');
subplot(2,2,2)
plot(err_iekf(2,:))
title('迭代EKF控制误差')
ylabel('theta dot');
subplot(2,2,3)
plot(err_ukf(2,:))
title('UKF控制误差')
ylabel('theta dot');
subplot(2,2,4)
plot(err_iukf(2,:))
title('迭代UKF控制误差')
ylabel('theta dot');P_ekf2 = reshape(P_ekf, [4, Times1]);
P_iekf2 = reshape(P_iekf, [4, Times1]);
P_ukf2 = reshape(P_ukf, [4, Times1]);
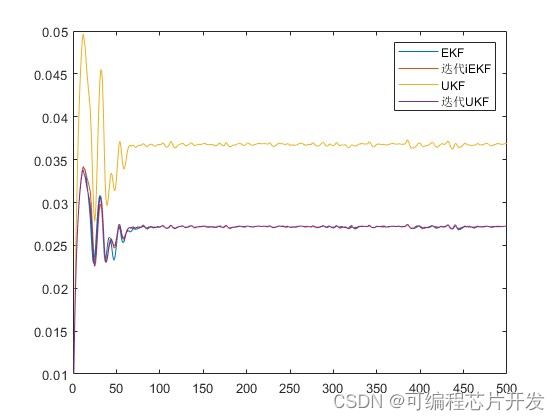
P_iukf2 = reshape(P_iukf, [4, Times1]);figure;
plot(P_ekf2(1,:))
hold on
plot(P_iekf2(1,:))
hold on
plot(P_ukf2(1,:))
hold on
plot(P_iukf2(1,:))
legend('EKF','迭代iEKF','UKF','迭代UKF')
0007
4.系统原理简介
倒立摆控制系统是一种具有挑战性的非线性控制系统,常用于研究控制算法的性能。扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)是两种常用的非线性滤波方法,用于估计系统的状态。本文将详细介绍基于迭代扩展卡尔曼滤波算法的倒立摆控制系统,并对比UKF、EKF迭代UKF和迭代EKF的性能。
4.1、UKF(无迹卡尔曼滤波)
UKF是一种基于无迹变换(Unscented Transform,UT)的非线性滤波方法。它通过选择一组确定的sigma点来逼近非线性函数的概率密度函数,从而避免了EKF中对非线性函数进行泰勒级数展开带来的截断误差。


4.2 EKF(扩展卡尔曼滤波)
EKF是一种基于泰勒级数展开的非线性滤波方法。它通过在当前估计值附近对非线性函数进行泰勒级数展开,并保留一阶项来近似非线性函数。然后利用卡尔曼滤波的框架进行状态估计。

4.3iEKF(迭代扩展卡尔曼滤波)
iEKF是一种基于迭代思想的扩展卡尔曼滤波方法。它通过多次迭代来改进状态估计的精度。在每次迭代中,利用上一次迭代的估计值对非线性函数进行泰勒级数展开,并更新状态估计,IEKF 的核心思想就是想 提高观测方程的线性化精度,因为我们之前的 EKF 都是把观测方程在IMU得到的 先验状处进行线性化,此时线性化是观测方程为:
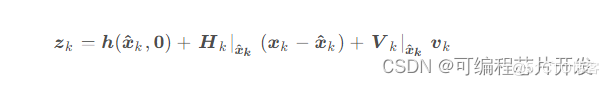
4.4 iUKF(迭代无迹卡尔曼滤波)
iUKF结合了无迹卡尔曼滤波和迭代思想,通过多次迭代来改进状态估计的精度。在每次迭代中,利用上一次迭代的估计值重新计算sigma点,并通过无迹变换传播sigma点来更新状态估计。
4.5优缺点比较
UKF和iUKF相较于EKF和iEKF,由于采用了无迹变换,对于非线性函数的逼近更为准确,因此在非线性较强的系统中表现更好。然而,UKF和iUKF的计算复杂度相对较高,对于维数较高的系统可能会面临计算上的挑战。
另一方面,EKF和iEKF在线性化过程中只保留了一阶项,因此在非线性较强时可能会导致较大的估计误差。但是,它们的计算复杂度相对较低,对于维数较高的系统更为实用。此外,通过迭代的方式,iEKF和iUKF可以进一步提高状态估计的精度。
总结来说,选择UKF、EKF、iUKF还是iEKF取决于具体的系统特性和需求。在非线性较强且维数较低的系统中,UKF和iUKF可能是更好的选择;而在维数较高或对计算复杂度有限制的场景中,EKF和iEKF可能更为实用。