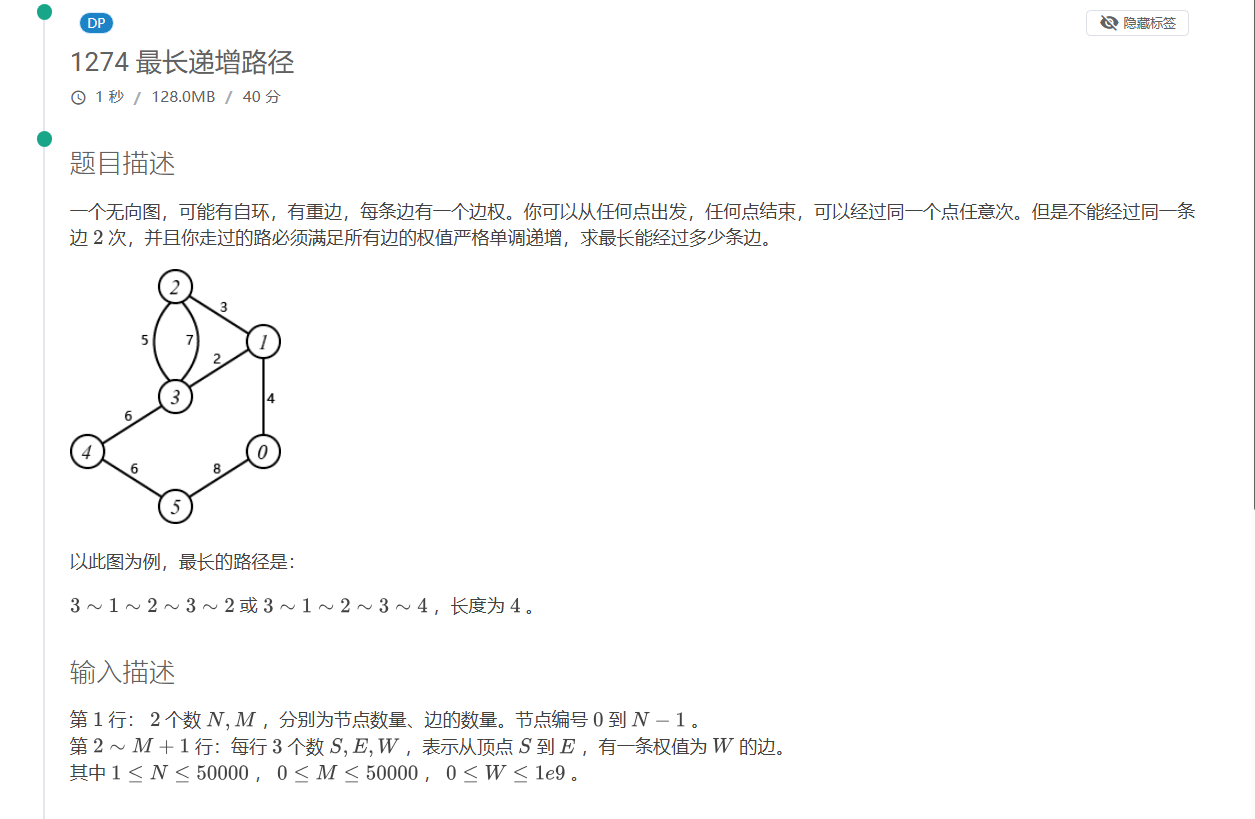
因为边权递增,按最小生成树的顺序 dp,设状态 \(dp[i]\) 为 \(i\) 点的最长路径长度,但是需要单调递增,所以考虑可以同时更新(先将原dp数组储存下来,再用新数组的值更新原 dp 数组),答案为 \(max(dp[i])\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e5+10;
int n,m;
struct ss{int u,v,w;
}e[N];
bool cmp(ss g,ss h){return g.w<h.w;
}
ll dp[N],f[N];
int main() { ios::sync_with_stdio(false);cin>>n>>m;for(int i=1;i<=m;i++){cin>>e[i].u>>e[i].v>>e[i].w; }sort(e+1,e+1+m,cmp);int last=0;for(int i=1;i<=m;i++){if(e[i].w==e[i+1].w){continue; }for(int j=last+1;j<=i;j++){f[e[j].u]=dp[e[j].u];f[e[j].v]=dp[e[j].v];}for(int j=last+1;j<=i;j++){dp[e[j].u]=max(dp[e[j].u],f[e[j].v]+1);dp[e[j].v]=max(dp[e[j].v],f[e[j].u]+1);}last=i;}ll ans=0;for(int i=0;i<n;i++){ans=max(ans,dp[i]);}cout<<ans;return 0;
}