手动用梯度下降法和随机梯度下降法实现一元线性回归

手动用梯度下降法实现一元线性回归

实验目的

本次实验旨在通过手动实现梯度下降法和随机梯度下降法来解决一元线性回归问题。具体目标包括：

1. 生成训练数据集，并使用matplotlib进行可视化。
2. 设计一个`LinearModel`类来实现一元线性回归的批量梯度下降法。
3. 使用matplotlib显示拟合结果。
4.  修改`LinearModel`类来实现随机梯度下降法，并重复上述实验步骤。

实验环境

Python版本：3.x
库：NumPy, Matplotlib

实验步骤

步骤1：准备数据

1. 生成100个训练样本，其中自变量\(X\)取值服从均值为0，方差为1的正态分布。
2. 设定因变量\(Y\)的关系式为\(Y = 4X + 3 + e_r\)，其中\(e_r\)为误差项，取值服从均值为0，方差为1的正态分布。
3. 使用Matplotlib绘制生成的数据点。

import numpy as np
import matplotlib.pyplot as plt# 设置随机种子以保证结果可复现
np.random.seed(0)# 生成100个训练样本
X = np.random.normal(loc=0, scale=1, size=100)  # X服从N(0,1)
e_r = np.random.normal(loc=0, scale=1, size=100)  # 误差项e_r服从N(0,1)
Y = 4 * X + 3 + e_r  # Y = 4*X + 3 + e_r# 使用matplotlib显示生成的数据
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='blue', label='Actual Data')
plt.title('Generated Data for Linear Regression')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

步骤2：定义LinearModel类

1. 定义一个`LinearModel`类，包含模型初始化、前向传播、损失计算、梯度计算和参数更新等方法。
2. 在类中实现批量梯度下降法的训练逻辑，通过设置最大迭代次数或验证集错误率来停止迭代。

class LinearModel:def __init__(self):self.w = np.random.randn()  # 初始化权重wself.b = np.random.randn()  # 初始化偏置bdef forward(self, X):""" 计算预测值 """return self.w * X + self.bdef loss(self, y_pred, y_true):""" 计算平均平方误差损失 """return np.mean((y_pred - y_true) ** 2)def gradient(self, X, y_pred, y_true):""" 计算梯度 """dw = 2 * np.mean((y_pred - y_true) * X)db = 2 * np.mean(y_pred - y_true)return dw, dbdef update(self, dw, db, learning_rate):""" 更新权重和偏置 """self.w -= learning_rate * dwself.b -= learning_rate * dbdef train(self, X, Y, epochs, learning_rate):""" 训练模型 """losses = []for epoch in range(epochs):# 前向传播y_pred = self.forward(X)# 计算损失loss = self.loss(y_pred, Y)losses.append(loss)# 计算梯度dw, db = self.gradient(X, y_pred, Y)# 更新参数self.update(dw, db, learning_rate)# 打印损失if epoch % 100 == 0:print(f'Epoch {epoch}: Loss {loss:.4f}')return losses# 使用上面的LinearModel类进行训练
model = LinearModel()
losses = model.train(X, Y, epochs=1000, learning_rate=0.01)# 绘制损失函数的变化情况
plt.figure(figsize=(8, 6))
plt.plot(losses, label='Loss over epochs')
plt.title('Training Loss Over Time')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()# 使用matplotlib显示拟合结果
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='blue', label='Actual Data')
plt.plot(X, model.forward(X), color='red', label=f'Fitted Line (w={model.w:.2f}, b={model.b:.2f})')
plt.title('Fitted Line on Generated Data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

步骤3：显示拟合结果

1. 使用Matplotlib绘制生成的训练数据点。
2. 使用Matplotlib绘制批量梯度下降法得到的拟合直线。

#绘制两种方法的损失函数曲线
plt.figure(figsize=(10, 6))
plt.plot(losses, label='Batch Gradient Descent Loss')
plt.plot(sgd_losses, label='Stochastic Gradient Descent Loss')
plt.title('Comparison of Training Loss Over Time')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()

#比较拟合直线
plt.figure(figsize=(10, 6))
plt.scatter(X, Y, color='blue', label='Actual Data')
plt.plot(X, model.forward(X), color='green', label=f'Batch GD Fitted Line (w={model.w:.2f}, b={model.b:.2f})')
plt.plot(X, sgd_model.forward(X), color='red', label=f'SGD Fitted Line (w={sgd_model.w:.2f}, b={sgd_model.b:.2f})')
plt.title('Comparison of Fitted Lines from Batch GD and SGD')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

步骤4：实现随机梯度下降法

1. 修改`LinearModel`类为`SGDLinearModel`类，使得每次迭代仅使用一个样本点来估计梯度并更新参数。
2. 使用新类重复步骤2和步骤3的操作。

class SGDLinearModel:def __init__(self):self.w = np.random.randn()  # 初始化权重wself.b = np.random.randn()  # 初始化偏置bdef forward(self, x_i):""" 计算单个样本的预测值 """return self.w * x_i + self.bdef loss(self, y_pred, y_true):""" 计算单个样本的平方误差损失 """return (y_pred - y_true) ** 2def gradient(self, x_i, y_pred, y_true):""" 计算单个样本的梯度 """dw = 2 * (y_pred - y_true) * x_idb = 2 * (y_pred - y_true)return dw, dbdef update(self, dw, db, learning_rate):""" 更新权重和偏置 """self.w -= learning_rate * dwself.b -= learning_rate * dbdef train(self, X, Y, epochs, learning_rate):""" 训练模型 """num_samples = len(X)losses = []for epoch in range(epochs):epoch_loss = 0indices = np.arange(num_samples)np.random.shuffle(indices)  # 打乱样本顺序for idx in indices:# 随机选择一个样本x_i = X[idx]y_i = Y[idx]# 前向传播y_pred = self.forward(x_i)# 计算损失loss = self.loss(y_pred, y_i)epoch_loss += loss / num_samples  # 平均损失# 计算梯度dw, db = self.gradient(x_i, y_pred, y_i)# 更新参数self.update(dw, db, learning_rate)losses.append(epoch_loss)# 打印损失if epoch % 100 == 0:print(f'Epoch {epoch}: Loss {epoch_loss:.4f}')return losses# 使用SGDLinearModel类进行训练
sgd_model = SGDLinearModel()
sgd_losses = sgd_model.train(X, Y, epochs=1000, learning_rate=0.01)# 绘制损失函数的变化情况
plt.figure(figsize=(8, 6))
plt.plot(sgd_losses, label='Loss over epochs (SGD)')
plt.title('Training Loss Over Time with SGD')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()# 使用matplotlib显示拟合结果
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='blue', label='Actual Data')
plt.plot(X, sgd_model.forward(X), color='red', label=f'Fitted Line (w={sgd_model.w:.2f}, b={sgd_model.b:.2f})')
plt.title('Fitted Line on Generated Data with SGD')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

实验结果分析

数据可视化

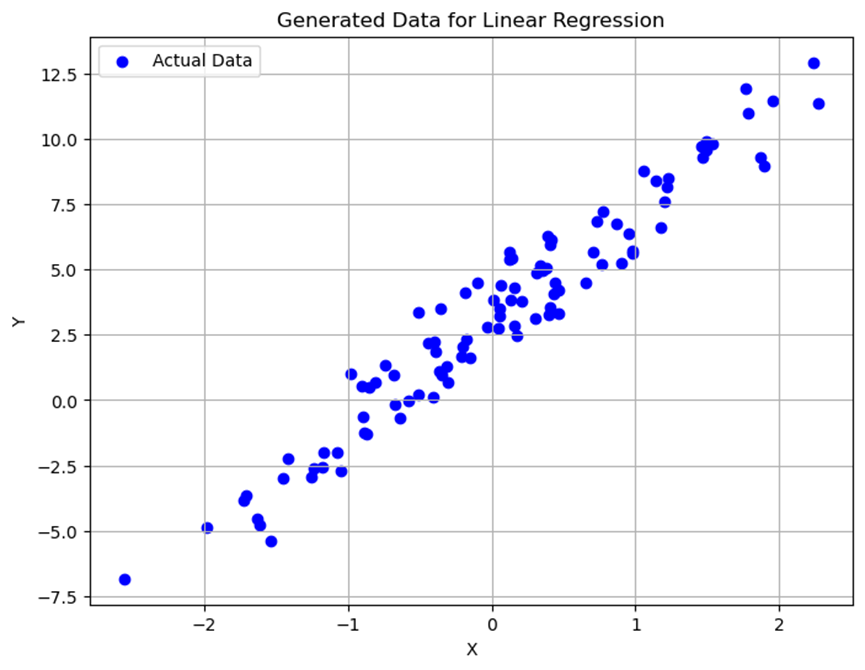
生成的训练数据点在二维坐标系中展示，可以看到数据点大致呈线性分布，但存在一定的噪声干扰。

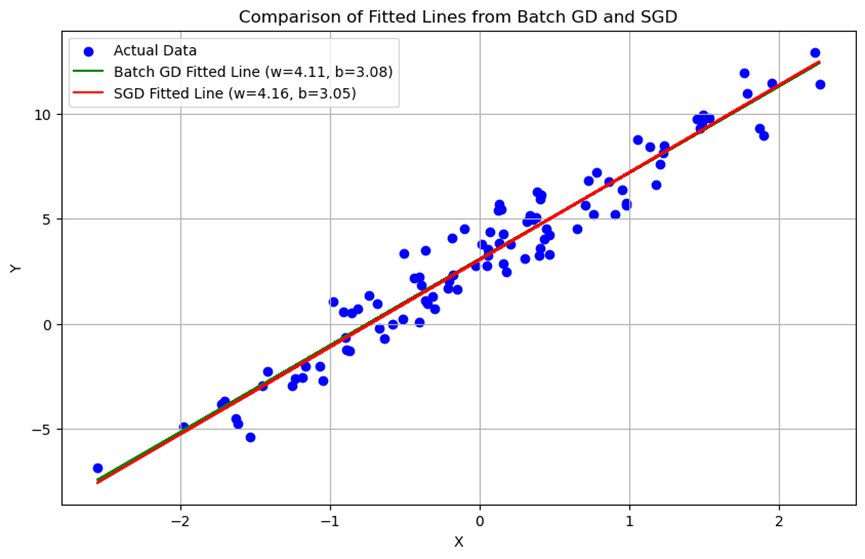
批量梯度下降法结果

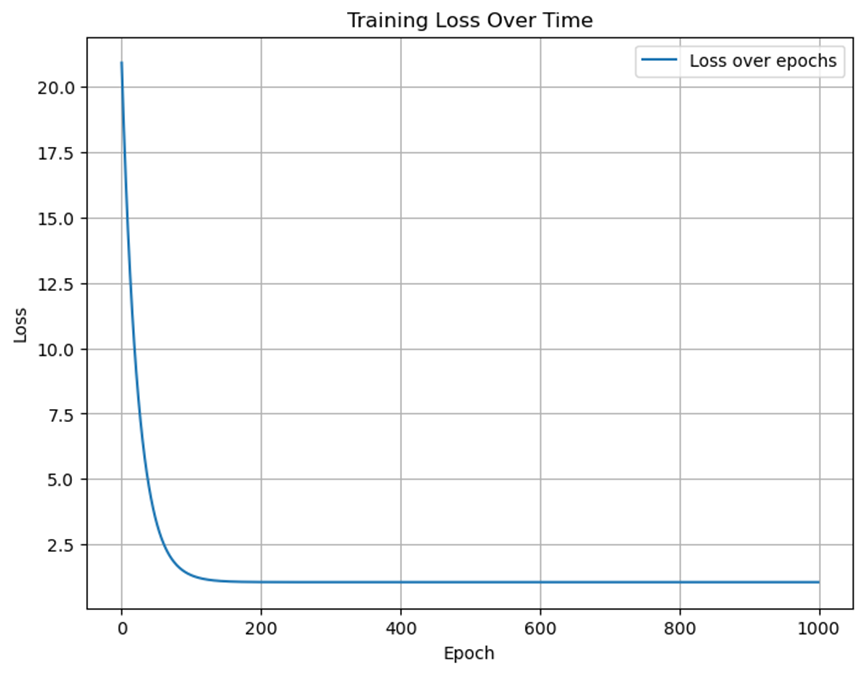
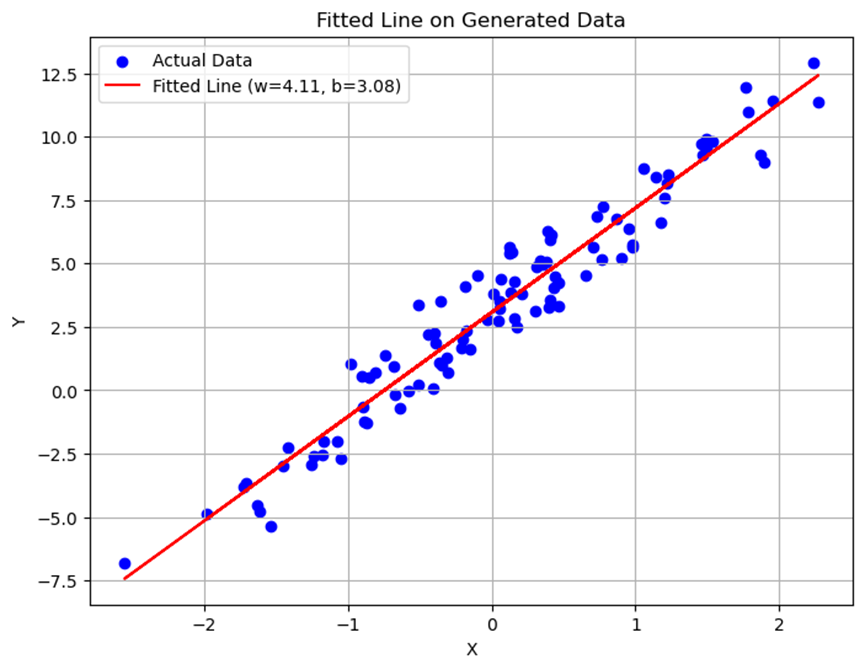
使用批量梯度下降法训练得到的模型能够较好地拟合训练数据，得到的拟合直线接近真实关系式\(Y = 4X + 3\)。

随机梯度下降法结果

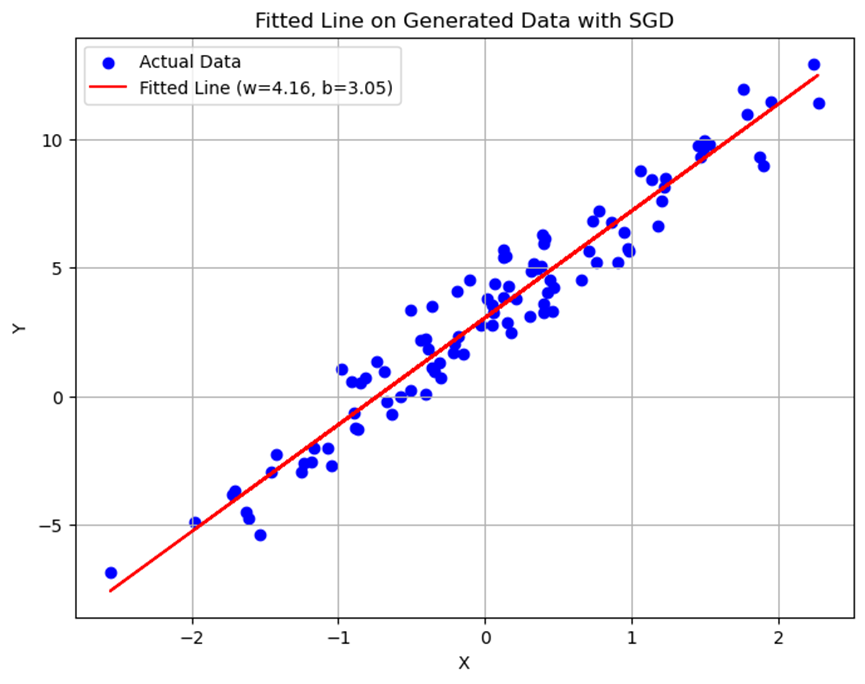
使用随机梯度下降法训练得到的模型同样能够拟合训练数据，但在训练过程中损失函数的变化更为波动。最终拟合直线与批量梯度下降法得到的结果相近。

损失函数对比

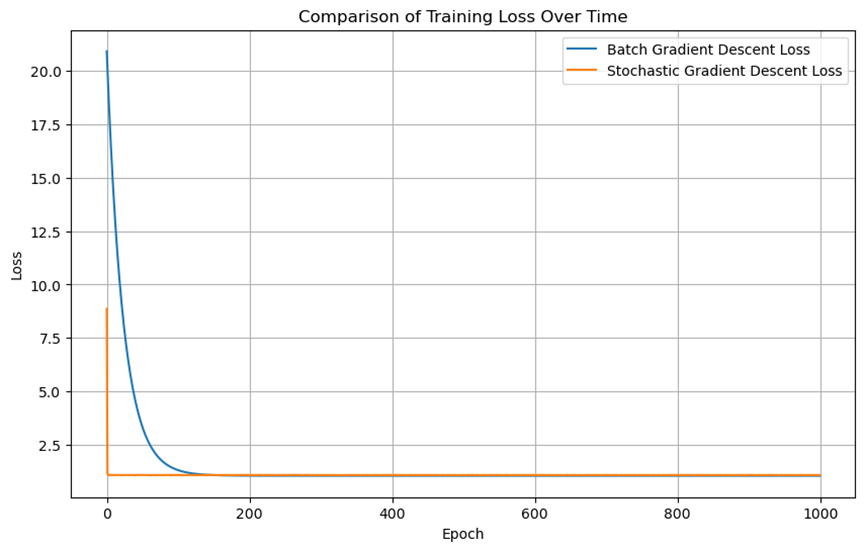
绘制两种方法的损失函数随迭代次数变化的曲线，可以看到随机梯度下降法的损失函数曲线更加波动，而批量梯度下降法的曲线较为平滑。

结论

通过本实验，我们成功实现了批量梯度下降法和随机梯度下降法来解决一元线性回归问题。两种方法都能有效地拟合数据，但在训练过程中表现出不同的特性。批量梯度下降法虽然收敛较慢，但训练过程更加稳定；而随机梯度下降法则收敛较快，但由于每次迭代仅使用一个样本点，因此训练过程更加波动。在实际应用中，可以根据具体需求选择合适的方法。