1 熵的概念
熵是热力学中的一个概念,由香浓引入到信息论中。在信息论中,熵是衡量随机变量不确定性的量度,熵越大表示随机变量的不确定性越大,即随机变量越难以预测。
2 熵的计算

信息熵的计算可以看笔者的博客:点此跳转。
3 最大熵原理定义
最大熵原理是一种选择随机变量统计特性最符合客观情况的准则,也称为最大信息原理。在信息论和概率统计中,熵用来表示随机变量不确定性的度量。最大熵原理认为,在只掌握关于未知分布的部分知识时,应该选取符合这些知识但熵值最大的概率分布。这种选择方法虽有一定的主观性,但可以认为是最符合客观情况的一种选择。
4 最大熵原理的实质
最大熵原理的实质是,在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断。这是我们可以作出的不偏不倚的选择,任何其它的选择都意味着我们增加了其它的约束和假设,这些约束和假设根据我们掌握的信息无法作出。
最大熵原理的直白解释就是:
在没有任何额外信息的情况下,你应该假设每种颜色的小球数量是尽可能“平均”的,也就是说,每种颜色的数量应该尽可能接近,以便让整个分布的不确定性最大化。
为什么这么做呢?因为当你假设每种颜色的数量都接近时,你就没有做任何额外的假设或猜测,你只是基于你已知的信息(总的小球数和颜色种类)来做出最不偏不倚的推断。这样的推断在不知道更多信息的情况下,是最合理的。
换句话说,最大熵原理就是告诉你,在不知道更多细节的情况下,选择那个让结果最“不确定”的选项,因为这样的选项最符合你当前的知识水平,没有引入任何不必要的偏见或假设。
在上面的例子中,如果你知道盒子里总共有9个小球,且只有红、黄、蓝三种颜色,那么按照最大熵原理,你会猜测每种颜色有3个小球,因为这样的分布不确定性最大(即,你无法准确预测下一个摸出来的小球会是什么颜色)。
当然,如果后来你得到了更多的信息(比如,有人告诉你红色小球的数量是蓝色小球的两倍),那么你就可以根据这些新信息来调整你的猜测,但在此之前,最大熵原理会指导你做出最合理的推断。
5 举例解释
5.1 示例一
假设有一个随机变量X,它有5个可能的取值{A, B, C, D, E},我们需要估计这5个取值的概率P(A), P(B), P(C), P(D), P(E)。这些概率值需要满足条件P(A) + P(B) + P(C) + P(D) + P(E) = 1。
-
无额外信息情况
如果没有其他信息,一个可行的办法就是认为这5个取值的概率都相等,即P(A) = P(B) = P(C) = P(D) = P(E) = 0.2。这种情况下,X的分布是均匀分布,其熵达到最大。 -
有额外信息情况
如果再添加一个条件,比如P(A) + P(B) = 0.3,那么我们需要重新估计这5个取值的概率,同时保持熵尽可能大。在这种情况下,我们可以选择使得P(A)和P(B)尽可能接近0.15(因为它们的和需要为0.3),同时保持P(C)、P(D)和P(E)尽可能相等,以使得整体分布的不确定性最大。
5.2 示例二
假设随机变量X有5个可能的取值:{A,B,C,D,E},我们需要估计这5个取值的概率P(A),P(B),P(C),P(D),P(E),且这些概率需要满足条件:P(A)+P(B)+P(C)+P(D)+P(E)=1
现在,我们得到了一个额外的信息:P(A)+P(B)=0.3。
-
应用额外信息
首先,我们根据额外信息设置P(A)和P(B)的和为0.3。为了简化计算,我们可以假设P(A)=P(B)(这不一定是最优解,但在这个例子中我们这样做是为了展示计算过程)。因此,
P(A)=P(B)=0.15 -
步骤 2: 分配剩余概率
接下来,我们需要为C,D,E分配剩余的概率,即1−0.3=0.7。为了使熵最大化,我们应该尽量使这三个概率相等。因此,
P(C)=P(D)=P(E)=7/30
步骤 3: 验证概率和
最后,我们需要验证所有概率的和是否为1:
P(A)+P(B)+P(C)+P(D)+P(E)=(0.15+0.15)+(7/30+7/30+7/30)=1
验证成功,说明我们的分配是合理的。 -
熵的计算(可选):
虽然题目没有直接要求计算熵,但我们可以计算这个分布的熵来验证它是否足够大(在这个上下文中,“大”是相对的,因为我们没有与其他可能的分布进行比较)。熵的计算公式为:
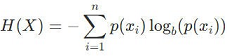
将我们的概率值代入公式,得到:
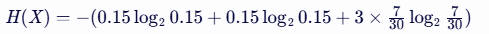
注意:这里的对数底数为2,但在实际应用中,有时也会使用自然对数(底数为e)。
计算得到的熵值将表明这个分布的不确定性程度。在这个例子中,由于我们尽量使概率分布均匀(在给定条件下),所以得到的熵值应该是相对较大的。然而,需要注意的是,这个熵值并不是在所有可能的分布中都是最大的,因为它受到了额外信息的约束。
6 结语
如有错误请指正,禁止商用。