·2024-9-11 ·最后更新时间 2024-9-11
作者学会了一个叫做\(Johnson\)的算法,所以就有了这篇博客......
Johnson算法是一个高效处理全源最短路的算法 其实也很慢,但目前是最高效的 为了更加方便你们接下来的学习我希望你们已经掌握了基本的最短路算法(SPFA,Dijsktra,Bellman-Ford,Floyd)如果没有掌握建先去学习一下qwq,
1.算法思路
我们知道通过Bellman-Ford我们可以在 \(O(n^2m)\) 的时间复杂度内求出两点之间的最短路,也可以通过类似动态规划的Floyd在 \(O(n^3)\) 的时间复杂度内求出两点最短路径,但是我们可以发现如果我们对于每个点跑一次 堆优化 Dijkstra最后的时间复杂度是 \(O(n*mlogn)\) 这是比Bellman-Ford算法要快的!!!但是,Dijkstra处理不了负边权啊,"那我们可以给所有边加上一个数字让他变成正数啊qwq" 什么时候蹿出来的 这个可能是大部分人第一时间的想法,但是并不如此,比如这样一个图:
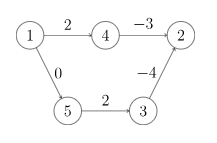
\(1->2\) 的最短路显然是 \(1->5->3->2\) 为 \(-2\)
但是当我们给所有边的边权都加上 \(5\) 最短路就变成了 \(1->4->2\) 这并不是我们想要的结果QAQ
那么有什么办法可以使得最后的最短路大小不变呢?
我们可以设一个超级源点并向其他所有点连一个长度为 \(0\) 的边:
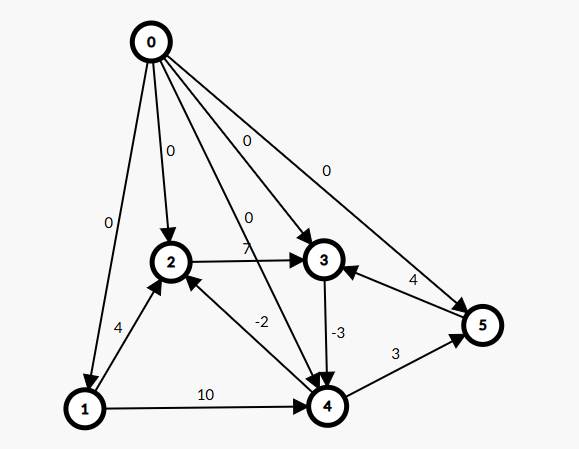
然后求出所有点到 \(0\) 的最短路:
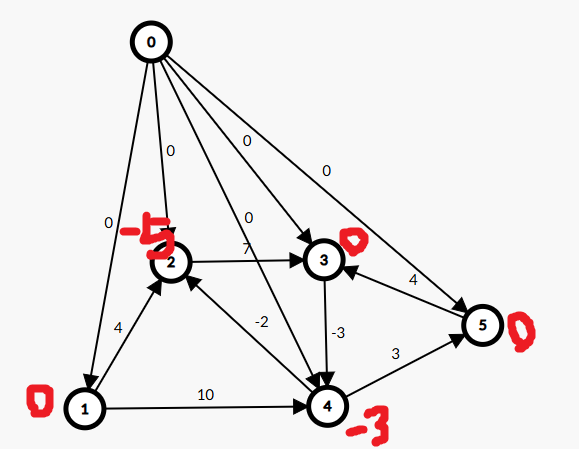
我们设最短路答案为 \(h_i\) 然后对于每条边我们让 \(w+h_i-h_j\) 就好啦qwq